Определение натуральной длины отрезка прямой

И углов ее наклона к плоскостям проекций

 

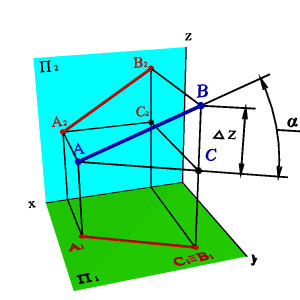
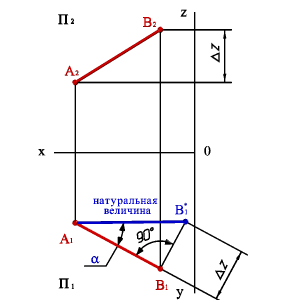
Длину отрезка АВ и a - угол наклона отрезка к плоскости П₁ можно определить из прямоугольного треугольника АВС | AС |=| A ₁ B ₁|, | СB =|DZ. Для этогона эпюре (рис.13) из точки B ₁ под углом 90⁰ проводим отрезок | B ₁ B ₁*|=DZ, полученныйв результате построений отрезок A ₁ B ₁ * и будет натуральной величиной отрезка АВ, а угол B ₁ A ₁ B ₁*=a. Рассмотренный метод называется методом прямоугольного треугольника.

а) модель	б) эпюр
Рисунок 13. Определение натуральной величины отрезка и угла его наклона к горизонтальной плоскости проекций

Длину отрезка АВ и b -угол наклона отрезка к плоскости П₂ можно определить из прямоугольного треугольника АВС | AС |=| A ₂ B ₂|, | СB |=DY. Построения аналогичные рассмотренным, только в треугольнике АВВ * сторона |BВ * |=DU и треугольниксовмещается с плоскостью П ₂ (рис. 14).

а) модель	б) эпюр
Рисунок 14. Определение натуральной величины отрезка и угла его наклона к фронтальной плоскости проекций

Отображение взаимного положения двух прямых

Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай.

Параллельные прямые линии.

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек. Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если ABCD то A₁B₁C₁D₁; A₂B₂C₂D₂; A₃B₃C₃D₃ (рис.15). В общем случае справедливо и обратное утверждение.

а) модель	б) эпюр
Рисунок 15. Параллельные прямые

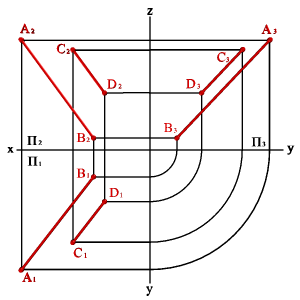
Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций (рис.16). В рассмотренном случае проекции отрезков на плоскость П₃ пересекаются, следовательно, они не параллельны.

а) модель	б) эпюр
Рисунок 16. Прямые параллельные профильной плоскости проекций

Пересекающиеся прямые.

Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку. Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи (рис.17).

а) модель	б) эпюр
Рисунок 17. Пересекающиеся прямые

 

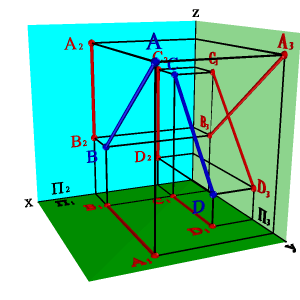
В общем случае справедливо и обратное утверждение, но есть два частных случая:

1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например, профильной (рис.18), то по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВ и СД пересекаются, причем точка пересечения проекций лежит на одной линии связи, однако сами отрезки не пересекаются, потому что точка пересечения профильных проекций этих отрезков не лежит на одной линии связи с точками пересечения их горизонтальной и фронтальной проекций.

а) модель	б) эпюр
Рисунок 18. Одна из прямых параллельна профильной плоскости проекций

2. Пересекающие прямые расположены в общей для них проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций (рис.19).

О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции (А ₁ В ₁∩ С ₁ D ₁Þ АВ∩СD).

 

а) модель	б) эпюр
Рисунок 19. Пересекающиеся прямые расположены в фронтально проецирующей плоскости

Скрещивающиеся прямые

Скрещивающимися называются две прямые не лежащие в одной плоскости.