Пересечение поверхностей плоскостями

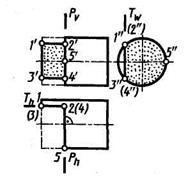
Форму деталей часто образуют срезом или вырезом части ма­териала плоскостями из исходных тел — заготовок, ограничен­ных криволинейными поверхностями. При этом возникает необходимость построения на чертеже проекций линии пересече­ния поверхности плоскостью. Такие же линии строят на чертежах деталей, поверхности которых ограничены пересекающимися между собой участками плоскости и поверхности.

В случае пересечения линейчатой поверхности плоскостью линия пересечения может быть кривой или прямой.

Для построения линии пересечения линейчатой поверхности плоскостью в общем случае строят точки пересечения прямоли­нейных образующих поверхности с секущей плоскостью, т. е. на­ходят точки пересечения прямой с плоскостью. Искомую кривую проводят через эти точки.

Для построения линии пересечения линейчатой поверхнос­ти с плоскостью в общем случае применяют вспомогательные секущие плоскости. Точки искомой линии определяются в пе­ресечении линий, по которым вспомогательные секущие плос­кости пересекают данные поверхность и плоскость. Примеры применения вспомогательных плоскостей рассмотрены ниже.

При подборе вспомогательных плоскостей надо стремиться к упрощению построений. Если секущая плоскость — плоскость частного положения, то задача упрощается, так как одна проекция линии пересечения плоскости с кривой поверхностью уже имеется и совпадает со следом секущей плоскости. Построение недостающих проекций линии пересечения сводится к построению недостающих проекций точек на поверхности по заданным проекциям этих точек на одной из проекций поверхности.

Пересечение цилиндрической поверхности плоскостью. Для построения линии пересечения цилиндрической поверхности плоскостью в общем случае находят точки пересечения образую­щих с секущей плоскостью. При необходимости не исключается применение и вспомогательных секущих плоско­стей, пересекающих поверхность и плоскость.

Заметим, что любую цилиндрическую поверхность плоскость, расположенная параллельно образующей этой поверхности, пере­секает по прямым линиям (образующим).

Вид линии, образованной при пересечении плоскостью прямого кругового цилиндра, определяется положением плоскости относительно оси. Эта линия — окружность, если плоскость перпендикулярна оси; две прямые (проекции 1'2' и 3'4' на рисунке 62) или одна прямая (касатель­ная), если плоскость параллельна оси (след P_w); эллипс (1—2—3—4 на рисунке 63), если плоскость располо­жена под углом к оси.

Образование выреза на цилинд­ре двумя плоскостями Р (P_v) || W и T(T_W) || V показано на рисунке 64.

 

Рисунок 62	Рисунок 63	Рисунок 64

 

Цилиндр с наклонным срезом. Рассмотрим построение чертежа ци­линдра со срезом проецирующей плоскостью под некоторым углом к его оси (не равным 0° и 90°), нату­ральной величины среза (рисунок 65).

 

 

Рисунок 65

 

Ось цилиндра и вся цилиндричес­кая поверхность перпендикулярны плоскости Н. Следовательно, все точ­ки цилиндрической поверхности, в том числе и линия пересечения ее с плоскостью Р (P_v) проецируются на плоскость Н в окружность. На ней от­мечают горизонтальные проекции то­чек 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12 эллипса, расположив их равномер­но по окружности. В проекционной связи строят фронтальные проекции 1', 2', 3', 4', 5', 6', 7', 8', 9', 10', 11' и 12' отмеченных точек на фронтальном следе Р_V, се­кущей плоскости. Профильные проекции тех же точек строят по их горизонтальной и фронтальной проекциям на линиях связи.

Профильная проекция линии пересечения цилиндра с се­кущей плоскостью – эллипс, большая ось 10"4" которого в данном случае равна диаметру цилиндра, а малая 1"7" — про­фильная проекция отрезка 1—7.

Натуральный вид фигуры сечения цилиндра плоскостью Р построен способом перемены плоскостей проекций на плоско­сти S, перпендикулярной плоскости V.

Пересечение конической поверхности плоскостью. При пересечении конической поверхности вращения плос­костью получаются различные линии — прямые, замкнутые кривые — окружности и эллипсы, незамкнутые кривые — па­раболы и гиперболы, а также точка. Вид указанных линий определяется положением секущей плоскости относительно вершины конической поверхности и соотношением между ве­личинами углов наклона секущей плоскости и образующей ко­нической поверхности к ее оси.

Если секущая плоскость Р (P_v) проходит через вершину (рисунок 66, а), то пересечение плоскости с конической поверх­ностью в зависимости от угла α наклона плоскости к оси по­верхности образует:

при β < α < (180° – β) - точку;

при α = β— прямую, по которой плоскость касается кони­ческой поверхности;

при 0 α < β — две прямые (образующие). Если плоскость пересекает коническую поверхность и при этом не проходит через вершину, то в их пересечении имеют место (рисунок 66, б, в):

при α = 90° — окружность (плоскость, перпендикулярная оси)– рисунок 66, б);

при β < α <(180°– β) – эллипс — рисунок 66, б — плоскость пересекает все образующие конической поверхности;

при α < β — гипербола (плоскость параллельна двум образу­ющим и пересекает коническую поверхность по обе стороны от вершины — рисунок 79, в);

при α = β — парабола (плос­кость, параллельная одной из об­разующих — рисунок 66, в).

Рисунок 66

 

Рисунок 67

 

Наглядное изображение кри­вых — эллипса, гиперболы, па­раболы, получающихся при пере­сечении конической поверхности плоскостями Q, T, R, приведено на рисунке 67.

Пересечение конуса с плоско­стью. Для построения кривой ли­нии, получаемой при пересечении конической поверхности плоскостью, в общем случае находят точки пересечения прямоли­нейных или круговых образующих конической поверхности с секу­щей плоскостью. Соответствующий пример в случае пересечения фронтально-проецирующей плоскостью Р (P_v) конуса с вершиной S приведен на рисунке 68. Построение линии пересечения плоскости с конической поверхностью обыч­но выполняют в следующем порядке. Основание конуса делят на несколько равных частей (обычно 12), проводят горизон­тальные проекции s—1, s—2,..., s—12 образующих и строят их фронтальные проекции. На фронтальной проекции отмечают фронтальные проекции точек пересечения построенных обра­зующих на видимой поверхности конуса с секущей плоскостью Р (P_v): с', d', f', q', а также крайних точек а' и b'. Горизон­тальные проекции строят в проекционной связи на соответ­ствующих проекциях образующих — точки а, с, d, f, q, b на проекциях образующих s—1, s—2, s—3, s—5, s—6, s—7, а так­же симметричные им точки на проекциях образующих s—12, s—11, s—9, s—8. Горизонтальную проекцию е точки Е на об­разующей S—4 и симметричной точки на образующей S—10 строят с помощью окружности радиуса е'е₁', проведенной на поверхности конуса.

На фронтальной проекции большая ось АВ эллипса — линии пересечения фронтально-проецирующей плоскости с кону­сом — проецируется в натуральную величину. Ма­лая ось MN эллипса перпендикулярна большой и проецируется в точку т'(п') в середине фронтальной проекции а'b' боль­шой оси.

Построение горизонтальной проекции малой оси эллипса выполнено с помощью параллели с проекциями т'14' и т — 14 — п. Горизонтальная проекция тп малой оси эллипса построена в проекционной связи как хорда горизонтальной проекции т—14—п этой параллели. Профильная проекция ли­нии среза конуса также построена по фронтальной и горизон­тальной проекциям точек в проекционной связи.

Отметим, что на профильной проекции точки а"и b" низ­шая и высшая, m"и n" – крайние (правая и левая), е" исим­метричная ей — точки касания проекций крайних образующих.

Построение натурального вида фигуры среза вы­полнено по координатам в системе координат х_ь у_х.

 

Рисунок 68