Взаимно перпендикулярные плоскости

 

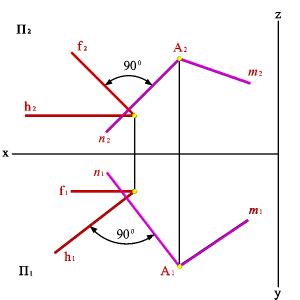
Частный случаем пересечения плоскостей являются взаимно перпендикулярные плоскости.

Известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей, перпендикулярных данной плоскости a(h,f). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a. Для того, чтобы через точку А провести плоскость, перпендикулярную плоскости a(h, f),необходимо из точки А провести прямую n, перпендикулярную плоскости a(h, f), (горизонтальная проекция n₁ перпендикулярна горизонтальной проекции горизонтали h₁, фронтальная проекция n₂ перпендикулярна фронтальной проекции фронтали f₂). Любая плоскость, проходящая через прямую n будет перпендикулярна плоскости a(h, f), поэтому для задания плоскости через точку А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми (m, n),будет перпендикулярна плоскости a(h, f) (рис. 39).

а) модель	б) эпюр
Рисунок 39. Взаимно перпендикулярные плоскости

3.6. Отображение относительного положения прямой и плоскости

Известны три варианта взаимного расположения прямой и плоскости:

1. Прямая принадлежит плоскости.

2. Прямая параллельна плоскости.

3. Прямая пересекает плоскость.

Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.

3.6.1. Параллельность прямой и плоскости

При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости и не принадлежит этой плоскости.

Пусть дана плоскость общего положения ABC и прямая общего положения а. Требуется оценить их взаимное положение (рис. 40).

Для этого через прямую а проведем вспомогательную секущую плоскость g - в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостей g и АВС - прямую п (DF).Проекция прямой п на горизонтальную плоскость проекций совпадает с проекцией а₁ и со следом плоскости g. Проекция прямой п₂ параллельна а₂, п₃ параллельна а₃, следовательно, прямая а параллельна плоскости AВС.

 

а) модель	б) эпюр
Рисунок 40. Прямая параллельная плоскости

3.6.2. Пересечение прямой с плоскостью

Нахождение точки пересечения прямой линии и плоскости – одна из основных задач начертательной геометрии.

Пусть дана плоскость AВС и прямая а. Требуется найти точку пересечения прямой с плоскостью и определить видимость прямой по отношению к плоскости.

Алгоритм решения задачи (рис. 41) следующий:

1. Через горизонтальную проекцию прямой а₁ проведем вспомогательную горизонтально проецирующую плоскость g.

2.

а) модель	б) эпюр
Рисунок 41. Нахождение точки пересечения прямой и плоскости

3. Находим линию пересечения вспомогательной плоскости с заданной. Горизонтальный след плоскости g₁ пересекает проекцию плоскости A₁В₁С₁ в точках D₁ и F₁, которые определяют положение горизонтальной проекции п₁ - линии пересечения плоскостей g и AВС. Для нахождения фронтальной и профильной проекции п спроецируем точки D и F на фронтальную и профильную плоскости проекций.

4. Определяем точку пересечения прямых а и п. На фронтальной и профильной проекциях линия пересечения плоскостей п пересекает проекции а в точке К, которая и является проекцией точки пересечения прямой а с плоскостью AВС, по линии связи находим горизонтальную проекцию К₁.

5. Методом конкурирующих точек определяем видимость прямой а по отношению к плоскости AВС.

3.6.3. Перпендикулярность прямой и плоскости

Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.

Прямая считается перпендикулярной плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим ей. В качестве таких прямых удобно принимать горизонталь и фронталь. Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.

Верно и обратное: если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.

Рассмотрим решение задачи на построение перпендикуляра к плоскости из точки А (рис. 42).

а) модель	б) эпюр
Рисунок 42. Прямая, перпендикулярная плоскости

Пусть дана плоскость ВСD и точка А. Требуетсяпостроить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD.

В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А₁ прямую n₁ перпендикулярно горизонтальной проекции горизонтали h₁, а на фронтальной плоскости проекций через точку А₂ прямую n₂ перпендикулярно фронтальной проекции фронтали f₂, согласно, теореме о перпендикуляре к плоскости, полученная прямая n будет перпендикулярна плоскости ВСD.

ПРЕОБРАЗОВАНИЕ ЧЕРТЕЖА