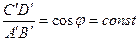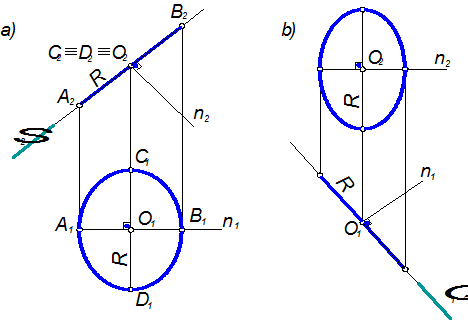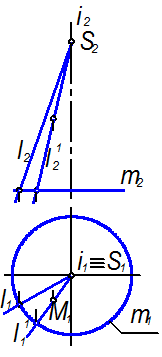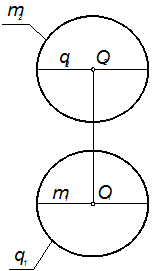Ортогональная проекция окружности

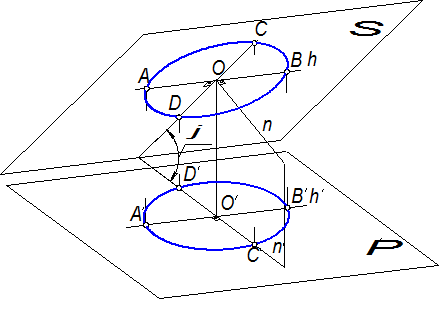
Как известно, параллельной проекцией окружности является кривая, называемая эллипсом. Поскольку ортогональная проекция является частным случаем параллельной, то очевидно, что ортогональной проекцией окружности будет тоже эллипс. Так, проецируя окружность, расположенную в плоскости S с центром в точке D, ортогонально на плоскость П¢, получим эллипс с центром в точке D¢ в соответствии с рисунком 1.3.28.

Рассмотрим в окружности два взаимно перпендикулярных диаметра AB и CD, причём АВ проходит по прямой уровня плоскости S (по прямой h), т.е. АВ||П¢. Следовательно, А¢В¢=АВ=d, где d – диаметр окружности. Диаметр CD как перпендикулярный к АВ, являющийся линией уровня плоскости S, называется также линией наибольшего наклона данной плоскости к плоскости проекций П¢. Такое название объясняется тем, что среди различных прямых плоскости S линия наибольшего наклона CD, перпендикулярная к линии уровня АВ, образует наибольший угол с плоскостью проекций П¢. Угол j, образованный диаметром окружности CD и диаметром эллипса C¢D¢ как проекцией CD, является линейным углом двугранного угла наклона плоскости S к плоскости П¢. Тогда C¢D¢=CD · cosj, но CD=АВ=d, следовательно C¢D¢ = d · cosj.

Как известно, взаимно перпендикулярные диаметры окружности обладают свойством сопряжённости (каждый сопряжённый диаметр делит пополам хорды, параллельные другому диаметру), это свойство при параллельном проецировании сохраняется, следовательно, диаметры А¢В¢ и C¢D¢ будут сопряжёнными диаметрами эллипса.

 

 

Рисунок 1.3.29 – Ортогональная проекция окружности

 

Но с другой стороны, эти диаметры взаимно перпендикулярны, так как являются проекциями взаимно перпендикулярных диаметров, один из которых параллелен плоскости проекций, поэтому они являются осями эллипса, причём А¢В¢ – большая ось, C¢D¢ – малая ось.

Если провести какую-нибудь прямую n, перпендикулярную к плоскости S в соответствии с рисунком 1.3.29, то такая прямая будет перпендикулярна ко всякой прямой плоскости S, в частности, будет перпендикулярна к диаметру АВ||П¢. Поэтому её ортогональная проекция n¢ на плоскость П¢ окажется прямой, перпендикулярной к проекции А¢В¢ диаметра АВ. Иначе говоря, проекция прямой, перпендикулярной к плоскости S, параллельна малой оси эллипса.

Таким образом, большая ось эллипса, являющегося ортогональной проекцией окружности, плоскость S которой составляет угол j с плоскостью проекций, параллельна проекции линии уровня плоскости S и равна диаметру окружности, а малая ось параллельна проекции перпендикуляра к плоскости S и равна d·cosj.

Рассмотрим соотношение осей полученного эллипса:

Для данных плоскостей S и П¢ угол j и cosj – величины постоянные. Вследствие этого cosj может служить характеристикой отношения осей эллипса, которое, в свою очередь, характеризует форму эллипса.

Итак, как бы ни была расположена окружность в плоскости S, на плоскости проекций всегда будет получаться эллипс одной и той же формы. Следует отметить, что при данном угле j не только форма эллипса будет постоянной, но и расположение осей также не будет зависеть от размеров и положения окружности в плоскости S.

Если угол j увеличивать, то эллипс, имея постоянной большую ось, будет становиться всё уже. В пределе, когда угол j станет равным 90°, а cosj= 0, т.е. плоскость S перпендикулярна плоскости П¢, окружность будет проецироваться в отрезок.

Если cosj= 1, то плоскость S параллельна плоскости проекций и эллипс-проекция принимает форму окружности.

Рассмотрим построение окружности, расположенной в проецирующей плоскости в соответствии с рисунком 1.3.30, а.

Пусть окружность с центром в точке О и радиусом R лежит во фронтально проецирующей плоскости S (S₂). Выберем два взаимно перпендикулярных диаметра окружности АВ и CD, из которых АВ||П₂, а CD||П₁. Таким образом, диаметр CD совпадает с горизонталью плоскости S, а АВ – с линией наибольшего наклона к плоскости П₁.

Рисунок 1.3.30 ­­- Окружность в проецирующей плоскости

 

Тогда проекциями диаметра АВ будут служить отрезки А₁В₁ и А₂В₂=АВ=2R, диаметр CD спроецируется на П₂ в точку С₂ºD₂= 0, а на плоскость П₁ в отрезок С₁D₁=CD= 2 R.

Таким образом в данном случае фронтальной проекцией окружности является отрезок прямой длиной 2 R, горизонтальной проекцией – эллипс,

большой осью которого служит отрезок С₁D₁, малой осью – отрезок А₁В₁. Заметим, что малая ось А₁В₁ эллипса совпадает с проекцией n ₁ перпендикуляра n к плоскости S. Промежуточные точки эллипса можно построить при помощи двух концентрических окружностей, проведённых на осях С₁D₁ и А₁В₁ как на диаметрах.

Аналогично строят проекции окружности, расположенной в горизонтально проецирующей плоскости Q (Q₁), в соответствии с рисунком 1.3.30, б.

 

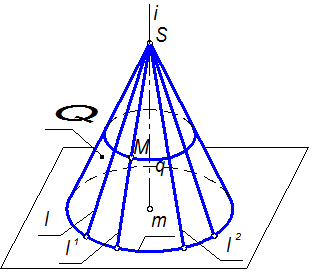
1.3.4 Образование, задание и изображение поверхностей

Начертательная геометрия пользуется преимущественно кинематическим способом образования поверхностей. Это означает, что поверхность образуется непрерывным перемещением линии (образующей) в пространстве по определённому закону. Тогда и сама поверхность будет непрерывной. Образующая может или сохранять свою форму при изменении положения, или непрерывно изменять и форму, и положение в пространстве.

Принадлежность поверхности некоторому классу описывается такими элементами, которые однозначно определяют её форму и размеры.

Совокупность элементов поверхности (параметров), выделяющих данную поверхность из всего класса поверхностей, к которому она принадлежит, будем называть определителем поверхности.

Например, конус вращения полностью задаётся осью и образующей в соответствии с рисунком 1.3.31. Поэтому определитель конической поверхности Q будет записан так: Q (i,l).

Задание оси i и образующей l конуса вращения позволяет построить этот конус. На нём можно провести любую другую прямолинейную образующую (l¹,l²,…) или окружность (q,m) поверхности, а также отметить произвольную её точку (М). Заметим, что этот способ задания конуса не является единственным.

Исходя из определителя поверхности конуса вращения, для задания конуса на чертеже достаточно задать проекции элементов определителя: i (l₁,i₂) и l (l₁,l₂) в соответствии с рисунком 1.3.32. Такой способ графического задания поверхности является метрически определённым и позволяет решать любые задачи на поверхности, а также её реконструировать.

 

Рисунок 1.3.31 – Конус вращения

 

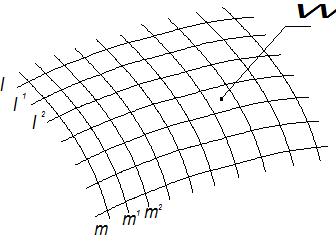
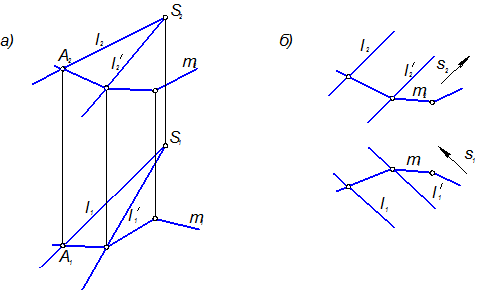
Закон перемещения в пространстве кривой (образующей), описывающий поверхность, удобно задавать некоторыми неподвижными кривыми, по которым скользит движущаяся образующая. Эти кривые, называемые направляющими линиями, часто входят в состав определителя поверхности.

Таким образом, на любой кинематической поверхности можно выделить два семейства кривых линий: семейство образующих (l) и семейство направляющих (m), каждое из которых покрывает всю поверхность и состоит из каких-либо линий (плоских или пространственных) в соответствии с рисунком 1.3.33.

Если поменять местами образующие и направляющие, т.е. принять m за образующие, а l – за направляющие, то в результате получится та же поверхность W.

Из кривых l¹,l²… и m¹,m²…, принадлежащих к указанным двум семействам линий, может быть составлен каркас кинематической поверхности.

Если учесть непрерывность перемещения образующей, а, следовательно, и непрерывность самой поверхности, то можно сделать очень важный для теории кинематических поверхностей вывод о том, что через любую точку поверхности можно провести пару кривых, принадлежащих двум различным семействам линий на поверхности.

Простейшей и основной задачей, входящей в виде элемента в решение любой более сложной задачи, является построение проекций точки, принадлежащей поверхности.

 

 

Рисунок 1.3.32 – Задание конуса вращения элементами определителя

 

Рисунок 1.3.33 – Каркас поверхности

 

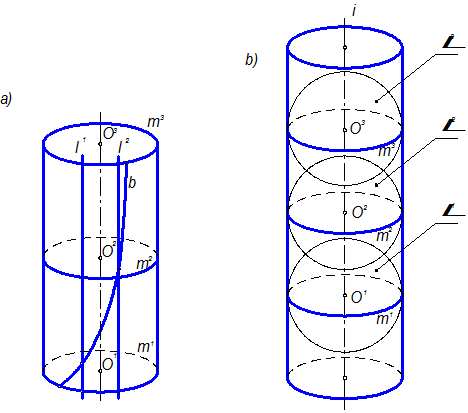
Общий метод заключается в том, что для построения второй проекции, например, М₂ точки М, лежащей на поверхности и заданной проекцией М₁, проводят через эту проекцию точки М линию l (l₁), принадлежащую одному из семейств линий на поверхности. Затем строят вторую проекцию l₂ этой линии и проводят через точку М₁ линию связи. Вторая проекция М₂ точки М будет лежать в пересечении проведённой линии связи с линией l₂. Выбор линии того или другого семейства основывается на графической простоте этой линии. На рисунке 1.3.32 использована прямолинейная образующая l¢.

Задание на чертеже кинематических поверхностей, определяемых несколькими точками или линиями, сводится к заданию проекций этих точек и линий. При этом надо иметь в виду некоторые условия, дополняющие чертёж.

Рассмотрим, например, образование поверхности цилиндра вращения. Определитель этой поверхности Q в соответствии с рисунком 1.3.34, а состоит из оси i (i₁,i₂) и образующей l (l₁,l₂): Q (i,l).

Цилиндр может быть образован также вращением кривой b, лежащей на его поверхности, или поступательным перемещением окружности m: m¹,m²,m³ …(поверхность переноса). В этих случаях определитель должен быть обозначен: Q (i,b), Q (i,m).

Кинематическая поверхность может быть образована также движением образующей поверхности, а не линии, как это было до сих пор. При этом движущаяся поверхность образует множество поверхностей, называемое семейством.

Из дифференциальной геометрии известно, что поверхность, касающаяся в каждой своей точке некоторой поверхности данного семейства, называется огибающей данного семейства.

Так, цилиндр вращения может быть образован как огибающая однопараметрического семейства сфер (L¹, L², L³ …) с центрами О¹, О², О³ …, расположенными на прямой i – оси цилиндра (рисунок 1.3.34, б).

 

Рисунок 1.3.34 – Способы образования цилиндра вращения

 

Этот цилиндр будет касаться сфер по окружностям больших кругов (m¹,m²,m²…), называемых характеристиками. Определитель поверхности

Q (i, R_L), где R_L – радиус образующей сферы.

На практике из всех возможных способов образования поверхности и вида образующих линий выбирают наиболее простые и удобные для решения задач.

Одним из основных требований, предъявляемых к чертежам в начертательной геометрии, наряду с обратимостью чертежа является его наглядность. Графическое задание поверхности проекциями элементов её определителя обеспечивает обратимость чертежа, но не обеспечивает его наглядности. Поэтому для увеличения наглядности изображения поверхности во многих случаях указывают на чертеже наряду с проекциями определяющих поверхность точек и линий также и очертание поверхности на плоскостях проекций.

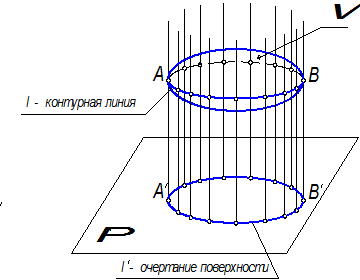
Предположим, что некоторая произвольная поверхность W проецируется на плоскость проекций П¢ в соответствии с рисунком 1.3.35. Тогда можно выделить те проецирующие лучи, которые будут касаться поверхности W и образовывать некоторую проецирующую цилиндрическую поверхность.

Линия l касания проецирующей поверхности и заданной называется контурной линией. Линия l¢ пересечения проецирующей поверхности с

плоскостью П¢ называется очертанием данной поверхности W.

Очертание поверхности получается, таким образом, как проекция контурной линии на данную плоскость проекций.

Очертание поверхности является границей видимости частей поверхности на данной плоскости. Оно отделяет область расположения проекций точек поверхности от всех других точек плоскости проекций. Поэтому при изображении поверхности на комплексном чертеже проекцию контурной линии на других плоскостях будем называть линией видимости.

 

 

Рисунок 13.35 – Очертание поверхности

 

На рисунке 1.3.36 изображена в двух проекциях сфера, очертания которой на плоскостях проекций П₁ и П₂ есть окружности q₁ и m₂. На другие плоскости проекций эти окружности проецируются в виде линий видимости q₂ и m₁ соответственно.

Рисунок 1.3.36 – Очертания и линии видимости сферы

На практике в различных областях техники получили широкое распространение следующие классы кинематических поверхностей:

1) поверхности вращения, которые образуются вращением произвольной

образующей вокруг неподвижной оси, в частности, поверхности вращения

второго порядка;

2) поверхности второго порядка общего вида;

3) линейчатые поверхности, которые могут быть образованы движением

прямолинейной образующей;

4) винтовые поверхности, образуемые винтовым движением произвольной

образующей, и, в частности, линейчатые винтовые поверхности – геликоиды;

5) циклические поверхности, которые могут быть образованы движением

окружности постоянного или переменного диаметра.

Следует отметить, что отдельные поверхности могут быть отнесены не к одному, а к нескольким классам.

Линейчатые поверхности

 

Линейчатой поверхностью называется поверхность, которая может быть образована движением прямой линии в пространстве. В зависимости от характера движения образующей получаются различные типы линейчатых поверхностей.

Если прямолинейная образующая при своём движении перемещается по ломаной направляющей, то такая поверхность является гранной. При этом, если прямолинейная образующая во всех положениях проходит через неподвижную точку S (вершину), то полученная поверхность является пирамидальной в соответствии с рисунком 1.3.37, а. Определитель этой поверхности Q (l,m,S). Если прямолинейная образующая при своём перемещении имеет постоянное направление, то такая поверхность называется призматической в соответствии с рисунком 1.3.37, б. Определитель данной поверхности S (l,m,s).

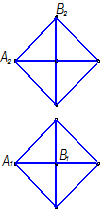
Рисунок 1.3.37 – Линейчатые гранные поверхности

Многогранники (пирамиды, призмы) – это замкнутые поверхности, образованные некоторым количеством граней. В данном случае и поверхность, и тело, ограниченное этой поверхностью, носят одно название. Элементами многогранника являются вершины, рёбра и грани; совокупность всех рёбер многогранника называют его сеткой. Построение проекций многогранника сводится к построению проекций его сетки.

Среди множества многогранников выделяют правильные многогранники. У таких многогранников все рёбра, грани и углы равны между собой. На рисунке 1.3.38, например, показан правильный многогранник, называемый октаэдром.

Среди криволинейных линейчатых поверхностей наибольшее распространение получили следующие типы поверхностей: конические, цилиндрические, с ребром возврата (торсы), с плоскостью параллелизма (поверхности Каталана), винтовые поверхности.

 

Рисунок 1.3.38 – Правильный многогранник

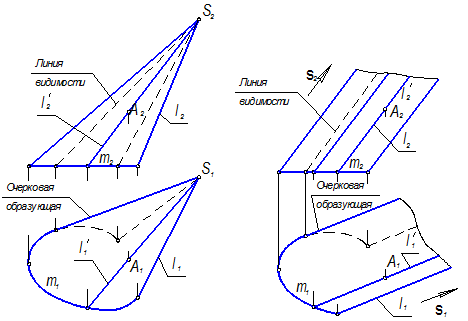
1.3.4.2 Коническая и цилиндрическая поверхности

Рисунок 1.3.39 – Коническая и цилиндрическая поверхности

Коническая поверхность образуется прямой линией l (образующей), перемещающейся вдоль кривой линии m (направляющей) и имеющей неподвижную точку S (вершину) в соответствии с рисунком 1.3.39, а. Определитель поверхности Q (l,m,S).

Цилиндрическая поверхность образуется прямой линией l (образующей), перемещающейся вдоль кривой линии m (направляющей) и имеющей постоянное направление s в соответствии с рисунком 1.3.39, б. Определитель поверхности S (l,m,s).

Поскольку все прямые, имеющие одно и то же направление, т.е. параллельные между собой, пересекаются в бесконечно удалённой (несобственной) точке, то цилиндрическую поверхность можно рассматривать как частный случай конической поверхности.

При задании конической и цилиндрической поверхностей на комплексном чертеже в качестве направляющей часто выбирают линию m пересечения поверхности с одной из плоскостей проекций.

Точки на поверхности (например, точку А на рисунке 1.3.39) строят при помощи проходящих через них образующих.

 

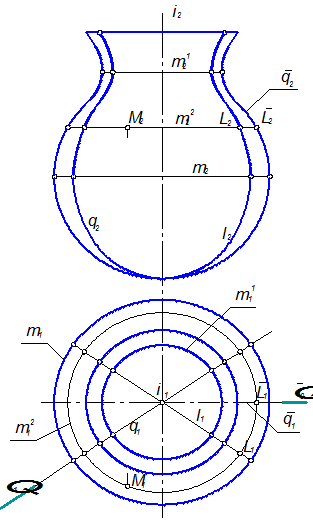
Поверхности вращения

Поверхностью вращения называется поверхность, которая описывается какой-либо образующей при её вращении вокруг неподвижной оси.

Образующая может быть как плоской, так и пространственной кривой. В частном случае это может быть прямая линия. Для задания поверхности вращения необходимо задать её ось i и какую-либо образующую l, лежащую на этой поверхности. Определитель поверхности вращения: Г (i, l). На чертеже она может быть задана проекциями этих элементов в соответствии с рисунком 1.3.40. Каждая точка L кривой l описывает при вращении окружность m с центром на оси i. Эти окружности называются параллелями поверхности. Кривые q, получающиеся в сечении поверхности вращения плоскостями Q (Q₁), проходящими через ось i, называются меридианами.

Поверхность симметрична относительно любой меридиональной плоскости, а все меридианы равны между собой. В соответствии с рисунком 1.3.40 образующая l лежит на одном из меридианов.

Если поверхность вращения расположить так, чтобы её ось i была перпендикулярна к плоскости проекций П₁, то все параллели спроецируются на эту плоскость без искажения. Меридиан q, расположенный во фронтальной плоскости Q (Q₁), называется главным меридианом. Он проецируется без искажения на плоскость проекций П₂ и определяет очертание поверхности на этой плоскости. Для построения очертания поверхности надо вращать точки образующей кривой l до их совпадения с плоскостью главного меридиана Q. В соответствии с рисунком 1.3.40 получена точка L, принадлежащая главному меридиану и, соответственно, очертанию поверхности. Именно таким образом строится очертание поверхности вращения по её определителю: в плоскость главного меридиана выводится определённое количество точек, соединяемых затем плавной кривой линией.

 

 

Рисунок 1.3.40 – Поверхность вращения

 

Параллели наибольшего и наименьшего радиусов называются соответственно экватором и горлом поверхности вращения. Они проецируются на плоскость П₁ в виде окружностей очертания. В соответствии с рисунком 1.3.40 это окружности m и m’.

Для построения точек, принадлежащих поверхности, можно использовать линии каркаса поверхности. Каркас поверхности вращения удобнее всего составлять из меридианов или параллелей, или из тех и других. Например, для нахождения второй проекции точки М (М₂), взятой на поверхности в соответствии с рисунком 1.3.40 следует провести через М₂ параллель m (m₂) и найти её горизонтальную проекцию m₁, на которой и будет находиться горизонтальная проекция М₁ точки М.