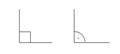Заочной формы обучения с применением

ВВЕДЕНИЕ

Начертательная геометрия, изучаемая студентами заочной формы обучения в первом семестре, является первой частью дисциплины «Инженерная графика» и её теоретической базой.

Данное учебно-методическое пособие посвящено именно этой части дисциплины. Вторая её часть будет отражена в последующих работах.

При изучении курса необходимо ознакомиться с программой, приобрести учебную литературу и тщательно продумать календарный план самостоятельной работы, согласуя его с учебным графиком и и планами по другим учебным дисциплинам первого курса. В этом плане начертательной геометрии следует уделить особое место, учитывая, что наряду с изучением теории необходимо ознакомиться с решением типовых задач каждой темы курса и выполнить контрольные работы.

Цели и задачи изучения дисциплины – уметь точно и аккуратно выполнять графические построения при решении конкретных графических задач. Правильно построенные самостоятельные занятия по начертательной геометрии разрешат трудности в изучении этой дисциплины и научат студента представлять всевозможные сочетания геометрических форм в пространстве. Начертательная геометрия способствует развитию пространственного воображения, умению «читать» чертежи, с помощью чертежа передавать свои мысли и правильно понимать мысли другого, что крайне необходимо инженеру.

При изучении начертательной геометрии следует придерживаться общих указаний:

1) Начертательную геометрию нужно изучать последовательно и систематически.

2) В начертательной геометрии следует избегать механического запоминания теорем, формулировок, решений задач. Такое запоминание непрочно. Студент должен разобраться в теоретическом материале и уметь применить его как общую схему к решению конкретных задач. Свои знания надо проверить ответами на вопросы включённых в это пособие контрольно-измерительных материалов и решением задач.

3) Каждую тему курса желательно прочитать дважды. При первом чтении изучается материал темы. При повторном чтении рекомендуется вести конспект, записывая в нём основные положения теории и порядок решения типовых задач.

4) В курсе начертательной геометрии решению задач должно быть уделено особое внимание. Решение задач является наилучшим средством более глубокого постижения положений теории. Прежде, чем приступить к решению задачи, надо понять её условие и чётко представить себе схему решения.

5) В начальной стадии изучения курса начертательной геометрии полезно прибегать к моделированию изучаемых геометрических форм и их сочетаний. Значительную помощь оказывают зарисовки воображаемых моделей, а также их простейшие макеты.

 

АВТОР-СОСТАВИТЕЛЬ:

Печенкина

Татьяна Владимировна

Старший преподаватель

 

СОАВТОРЫ:

Семено

Валерий Акимович

Доцент

 

 

Вильданова

Римма Гиниятовна

Старший преподаватель

 

 

Щеглова

Рима Азгаровна

доцент

 

РАБОЧАЯ ПРОГРАММА

по дисциплине

«Инженерная графика»

Начертательная геометрия является наукой о графических изображениях.

Различные инженерные сооружения их отдельные конструкции, архитектурные объекты, всевозможные машины и их детали выполняются по чертежам. Чертеж дает возможность определить пространственную форму изображенного предмета, взаимное расположение отдельных его деталей и выявить их истинные размеры.

Изображения на чертежах выполняется по правилам начертательной геометрии, поэтому изучение ее имеет большое значение в подготовке и творческом развитии будущего высококвалифицированного инженера любой специальности.

Основной задачей начертательной геометрии является изучение методов изображения пространственных форм на плоскости, а также примеры решения графическими способами различного рода задач, встречающихся в практике проектирования и конструирования, связанных с изменением, так и с определением взаимного расположения отдельных элементов проектируемого объекта.

Начертательная геометрия способствует развитию инженерного пространственного воображения, столь необходимого как при проектировании зданий и сооружений, так и при их возведении по готовым чертежам.

Студент должен знать:

- методы построения плоских геометрических моделей;

- методы проектирования и анализа поверхностей;

- методы решения позиционных и метрических задач;

- стандарты оформления и построения чертежей.

Студент должен уметь:

- выполнять простейшие геометрические построения при создании чертежей;

- выполнять и читать чертежи.

 

Содержание дисциплины

1. Общие положения и геометрические модели в ортогональных проекциях

(72 часа)

- центральное, параллельное, ортогональное проецирование;

- образование двухкартинного и трехкартинного комплексного чертежа;

- конкурирующие точки;

- ортогональные проекции геометрических объектов и позиционные задачи;

- изображение прямой на комплексном чертеже;

- прямые частного положения;

- следы прямой;

- определение натуральной величины отрезка прямой;

- взаимное положение двух прямых;

- теорема о проецировании прямого угла;

- изображение плоскости на комплексном чертеже;

- главные линии плоскости;

- взаимопринадлежность (инцидентность) точки и плоскости;

- следы плоскости;

- плоскости частного положения;

- параллельность прямой линии и плоскости;

- параллельность плоскостей;

- перпендикулярность прямой и плоскости;

- пересечение прямой линии с плоскостью;

- пересечение двух плоскостей;

- кривые линии;

- проекционные свойства плоских кривых;

- ортогональная проекция окружности;

- образование, задание и изображение поверхностей;

- линейчатые поверхности;

- гранная поверхность;

- коническая и цилиндрическая поверхности;

- поверхности вращения;

- поверхности вращения второго порядка;

- пересечение поверхности с плоскостью;

- конические сечения;

- пересечение поверхностей;

- способ вспомогательных секущих плоскостей-посредников;

- способ вспомогательных секущих концентрических сфер-посредников;

- особые случаи пересечения поверхностей второго порядка.

- преобразования комплексного чертежа;

- способ замены плоскостей проекций;

- способ плоскопараллельного перемещения;

- способ вращения вокруг проецирующей оси;

- построение разверток;

- развертка поверхностей многогранников;

- развертка поверхности призмы;

- развертка поверхности пирамиды;

- развертка развертываемых кривых поверхностей;

- развертка цилиндрической поверхности;

- развертка конической поверхности;

 

2. Геометрические модели в параллельных аксонометрических проекциях (4 часа)

- прямоугольная аксонометрия;

- стандартные аксонометрические системы;

- аксонометрическая проекция окружности.

 

 

Учебным планом по дисциплине «Начертательная геометрия» предусмотрены обзорные лекции по следующим темам (8 часов):

1. Способы проецирования. Двухкартинный и трехкартинный комплексный чертеж точки. Комплексный чертеж прямой. Определение натуральной величины отрезка методом прямоугольного прямоугольника.

2. Прямые частного положения. Взаимное положение прямых. Комплексный чертеж плоскости. Плоскости частного положения. Способы преобразования комплексного чертежа.

3. Поверхности – образование, задание и изображение. Способы вспомогательных секущих плоскостей и концентрических сфер-посредников.

4. Аксонометрические и перспективные проекции. Тени в ортогональных, аксонометрических и перспективных проекциях.

 

Обзорные практические занятия (8 часов):

1. Построение проекций точек по их координатам. Решение следующих задач: нахождение точки пересечения прямой и плоскости, нахождение прямой пересечения плоскостей, нахождение натуральных величин геометрических тел способами преобразования.

2. Построение линий пересечения поверхностей методом вспомогательных секущих плоскостей и концентрических сфер-посредников.

3. Построение теней в ортогональных проекциях. Аксонометрия, тени в аксонометрии.

4. Построение перспективы, тени в перспективе.

 

 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДИРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

 

 

ВОПРОСЫ ТЕОРИИ И ПРАКТИКИ

Инженерной графики

 

Электронное учебно-методическое пособие

по дисциплине «Инженерная графика»

для студентов специальностей

«Промышленное гражданское строительство» и

«Водоснабжение и водоотведение»

СОДЕРЖАНИЕ

 

	ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
1.1	Основные обозначения
1.2	Способы проецирования
1.2.1	Центральное проецирование
1.2.2	Параллельное проецирование
1.2.3	Ортогональное проецирование
1.2.4	Образование двух- и трёхкартинного комплексного чертежа
1.2.4.1	Конкурирующие точки
1.3	Ортогональные проекции геометрических объектов и позиционные задачи
1.3.1	Изображение прямой линии на комплексном чертеже
1.3.1.1	Прямые частного положения
1.3.1.2	Следы прямой линии
1.3.1.3	Определение натуральной величины отрезка прямой
1.3.1.4	Взаимное положение двух прямых
1.3.1.5	Теорема о проецировании прямого угла
1.3.2	Изображение плоскости на комплексном чертеже
1.3.2.1	Главные линии плоскости
1.3.2.2	Взаимопринадлежность (инцидентность) точки и плоскости
1.3.2.3	Следы плоскости
1.3.2.4	Плоскости частного положения
1.3.2.5	Параллельность прямой и плоскости
1.3.2.6	Параллельность плоскостей
1.3.2.7	Перпендикулярность прямой и плоскости
1.3.2.8	Пересечение прямой линии с плоскостью
1.3.2.9	Пересечение двух плоскостей
1.3.3	Кривые линии
1.3.3.1	Проекционные свойства плоских кривых
1.3.3.2	Ортогональная проекция окружности
1.3.4	Образование, задание и изображение поверхностей
1.3.4.1	Линейчатые поверхности
1.3.4.2	Коническая и цилиндрическая поверхности
1.3.4.3	Поверхности вращения
1.3.4.4	Поверхности второго порядка
1.3.4.5	Пересечение поверхности с плоскостью
1.3.4.6	Конические сечения
1.3.4.7	Пересечение поверхностей
1.3.4.7.1	Общий алгоритм решения задачи
1.3.4.7.2	Примеры пересечения поверхностей
1.3.4.7.3	Особые случаи пересечения поверхностей второго порядка
1.4	Преобразование комплексного чертежа
1.4.1	Способы замены плоскостей проекций
1.4.2	Основные задачи, решаемые способом замены плоскостей проекций
1.4.3	Способ плоскопараллельного перемещения
1.4.4	Способ вращения
1.4.4.1	Способ вращения вокруг проецирующей оси
1.4.4.2	Основные задачи, решаемые способом вращения
1.5	Построение разверток
1.5.1	Развертка поверхностей многогранников
1.5.1.1	Развертка поверхности призмы
1.5.1.2	Развертка пирамиды
1.5.2	Развертка развертываемых кривых поверхностей
1.5.2.1	Развертка цилиндрической поверхности
1.5.2.2	Развертка конической поверхности
	Геометрические модели в параллельных аксонометрических проекциях
2.1	Аксонометрические проекции
2.2	Стандартные аксонометрические системы
2.3	Аксонометрическая проекция окружности

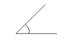
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

Основные обозначения

- Точки в пространстве обозначают прописными буквами латинского алфавита A, B, C, D… или арабскими цифрами 1, 2, 3, 4, 5 …

- прямые или кривые линии в пространстве – строчными буквами латинского алфавита a, b, c, d…

- плоскости и поверхности – прописными буквами греческого алфавита α, β, γ, δ,j…

- плоскости проекций при образовании комплексного чертежа – прописными буквами греческого алфавита с соответствующими индексами:

П₁ – горизонтальная плоскость проекций;

П₂ – фронтальная плоскость проекций;

П₃ – профильная плоскость проекций.

- проекции точек, прямых и плоскостей – соответствующей буквой с добавлением подстрочного индекса, характеризующего плоскость проекций:

на плоскости П₁ – А₁, а₁, α₁;

на плоскости П₂ – А₂, а₂, α₂;

на плоскости П₃ – А₃, а₃, α₃.

- совмещение геометрических элементов º, например a º b;

- взаимная принадлежность геометрических элементов Î, например А Î b;

- пересечение двух геометрических элементов Ç, например а Ç b;

- параллельность прямых //, например c // d;

- перпендикулярность геометрических элементов ^, например а ^ Σ;

- углы обозначаются строчными буквами греческого алфавита φ, ψ.

- графические обозначения углов

прямые углы углы

 

Способы проецирования

 

При помощи чертежей, то есть при помощи изображений на плоскости, изучаются пространственные формы предметов и соответствующие геометрические закономерности. Разработкой способов построения чертежей занимается начертательная геометрия. Её предметом является также изучение способов решения и исследования пространственных задач.

Поэтому к чертежам предъявляется ряд требований, наиболее существен­ными из которых, являются следующее:

1 Чертёж должен быть наглядным, т.е. он должен давать пространственное
представление изображаемого предмета.

2 Чертёж должен быть обратимым, т.е. таким, чтобы по нему можно было
точно воспроизвести форму и размеры изображаемого предмета.

3 Чертёж должен быть достаточно простым с точки зрения его графического
выполнения.

4 Графические операции, выполняемые на чертеже, должны давать достаточно
точные решения.

Для всех видов технических чертежей требование «обратимости» является особенно важным, т.к. чертёж есть производственный документ, по которому выполняется то или иное изделие. Поэтому необходимо, чтобы по чертежу можно было точно установить форму и размеры будущего изделия, а также не­которые другие данные о нём. Чертёж по определению Гаспара Монжа (1746-1818), французского учёного и инженера, одного из создателей начертательной геометрии, является "языком техника".

Для того, чтобы изображение предмета на плоскости позволяло точно определить его геометрическую фигуру, необходимо строить это изображение (чертёж) по определённым геометрическим правилам, позволяющим от плоских и, следовательно, искажённых форм на чертеже переходить к натуральным пространственным формам изображаемого предмета.

Такое геометрически закономерное изображение пространственного предмета на плоскости достигается при помощи метода проецирования, кото­рый является основным методом в начертательной геометрии.

Чертежи, построенные по методу проецирования, называются проекцион­ными.

Начертательная геометрия является той научной дисциплиной, которая помогает развитию пространственных представлений, необходимых не только в технике, но и вообще в практической жизни человека.

Центральное проецирование

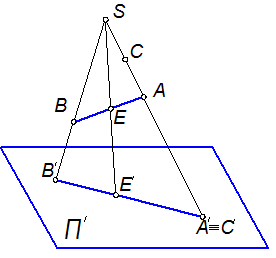
Пусть имеем в пространстве плоскость P′, которую будем называть плос­костью проекций (рисунок 1.2.1). Выберем некоторую точку S, не лежащую на плоско­сти проекций. Эту точку будем называть центром проецирования.

Рисунок 1.2.1 – Центральное проецирование

Для проецирования точки А пространства на плоскость P' надо провести через эту точку и центр проекций S прямую. Такая прямая называется проеци­рующей прямой. Находим затем точку пересечения проецирующей прямой SA с плоскостью проекций P′. Полученную точку пересечения А′ будем называть центральной проекцией данной точки А на плоскость П'.

В том случае, если точка А совпадает с центром проекций S, становится неопределённой не только проецирующая прямая, но и проекция точки на плоскость П′.

Таким образом, центр проекций S является исключительной точкой, не имеющей проекций.

Центральной проекцией прямой линии является прямая линия. Пусть тре­буется спроецировать центрально данную прямую АВ в соответствии с рисунком 1.2.1. Проецирующие прямые SA и SB определяют на плоскости П′ проекции А′ и В′ соответственно точек А и В. Для любой другой точки Е прямой АВ проецирующая прямая SЕ опре­деляет проекцию Е′. Все проецирующие прямые лежат в одной и той же (проецирующей) плоскости SAB. Поэтому все проекции точек данной прямой лежат на линии пересечения проецирующей плоскости SAB с плоскостью про­екций П′ _.

Если данная прямая проходит через центр проекций S, т.е. сама является проецирующей линией, то она проецируется на плоскость П′ в виде точки. Так, все точки прямой SA (рисунок 1.2.1) проецируются на плоскость П′ в одну и ту же точку А′. Например, точка С прямой SA даёт проекцию С′, совпадающую с А′.

Для построения проекций прямой линии достаточно построить проекции двух её точек. Это показывает, что для построения проекций фигуры не всегда необходимо проецировать все её точки. Например, для определения проекции треугольника достаточно построить проекции трёх его вершин.

Изображение предметов при помощи центрального проецирования от­личается большой наглядностью. Объясняется это устройством зрительного ап­парата человека, который с некоторым приближением можно считать работаю­щим по принципу центрального проецирования.

Параллельное проецирование

Наглядность - ценное свойство центрально проекционных изображений. Однако на практике большое значение имеют и другие качества проекционных чертежей, в частности, простота построения и обратимость. В этом отношении центрально проекционные чертежи не являются наиболее удобными. Поэтому большим распространением пользуется способ параллельного проециро­вания для построения изображений пространственных фигур.

Задаём некоторую плоскость П′, являющуюся плоскостью проекций, и направление проецирования s, не параллельное плоскости проекций П′ в соответствии с рисунком 1.2.2. Для проецирования какой-либо точки А пространства проводим через неё про­ецирующую прямую АА′, параллельную направлению проецирования s. Точка пересечения А′ проецирующей прямой с плоскостью П′ является параллельной проекцией точки А на плоскость П′.

Рисунок 1.2.2 – Параллельное проецирование

 

На рисунке 1.2.2 изображена операция параллельного проецирования отрезка АС. Проецирующие линии всех точек этого отрезка лежат в одной (проецирующей) плоскости. Поэтому проекцией отрезка АС является отрезок А'С' прямой линии. Это свойство общее для центральной и параллельной про­екций.

Рассмотрим некоторые свойства параллельного проецирования, которых не имеет центральная проекция.

1) Прямые, параллельные в пространстве (в общем случае) проецируются в виде прямых, параллельных на плоскости проекций П′.

Пусть имеем прямые АВ и CD, параллельные в пространстве (рисунок

1.2.3).

 

Рисунок 1.2.3 – Параллельная проекция параллельных в пространстве

прямых

Построив для прямых АВ и CD проецирующие плоскости AА¢В¢B и CС¢D¢D, заметим, что эти плоскости параллельны, как плоскости, имеющие уг­лы с соответственно параллельными сторонами (AB||CD; BВ¢ ||DD¢). Поэтому проецирующие плоскости пересекают плоскость проекций П' по двум парал­лельным между собой прямым.

2) Отношение отрезков, лежащих на параллельных прямых, со­храняется в параллельной проекции.

Пусть АВ и CD – отрезки, лежащие на параллельных прямых. Построим их проекции на плоскость П¢ при направлении проецирования s (рисунок 1.2.3). Про­ведём в проецирующих плоскостях отрезки А¢В1 и С¢D1, соответственно парал­лельные и равные отрезкам АВ и СD. Треугольники А¢B¢B1 и С¢D¢D1 являются подобными, т.к. их соответственные стороны параллельны. Отсюда

В частном случае данные отрезки АВ и CD могут оказаться лежащими на
одной прямой, однако это не изменит рассуждения.

Если при этом концы двух отрезков совпадают, т.е. имеем отрезки АВ и ВС в соответствии с рисунком 1.2.4, то вышеприведённое соотношение примет вид

Отсюда следует, что отношение, в котором точка В делит отрезок АС. со­храняется в проекции для точки В′, делящей отрезок А'С′.

 

Рисунок 1.2.4 – Деление отрезка в заданном соотношении при параллельном проецировании

 

3) Отношение проекции отрезка А'В' к натуральному отрезку постоянно для всех параллельных между собой отрезков.

Полученная выше пропорция после перестановки крайних членов имеет вид

Постоянное отношение u называется показателем искажения для отрезков данного направления

 

Ортогональное проецирование

Параллельное проецирование называется ортогональным (прямоугольным), если направление проецирования s перпендикулярно к плос­кости проекций П′ (s ^ П’).

В ортогональной проекции очень просто устанавливать соотношение ме­жду длиной натурального отрезка и длиной его проекции.

Пусть отрезок АВ образует с плоскостью проекций П' угол f (рисунок 1.2.5). Проведём A^′ В₁ параллельно АВ. Тогда

А'В'=А'В₁× cos j=АВ× cos j

Большое распространение ортогональные проекции получили в тех­нических чертежах, т.к. позволяют особенно легко судить о размерах изобра­жаемых предметов.

Рисунок 1.2.5 – Ортогональное проецирование

 

Образование двух- и трёхкартинного комплексного чертежа

Наиболее употребительным в практике является метод комплексного чертежа в ортогональных проекциях. Комплексным чертежом называется чертёж, состоящий из нескольких связанных между собой проекций изображаемой фигуры. Метод комплексного чертежа в ортогональных проекциях называется также методом Монжа.

Этот метод прост в построении и даёт большую точность при графическом решении задач. Он обеспечивает точное определение изображённой фигуры по чертежу. Недостатком метода является малая наглядность изображений.

Комплексный чертёж из двух проекций называется также двухкартинным чертежом.

Рассмотрим неподвижную систему двух взаимно перпендикулярных плоскостей П₁ и П₂ в соответствии с рисунком 1.2.6. Плоскость П₁, расположенная горизонтально, называется горизонтальной плоскостью проекций. Плоскость П₂, перпендикулярная к П₁, занимает вертикальное положение и расположена перед наблюдателем. Эту плоскость называют фронтальной плоскостью проекций. На обе эти плоскости будем проецировать ортогонально точки пространства.

Предположим, что в пространстве имеется некоторая точка А. Ортого­нальную проекцию А₁ точки А на плоскость П₁ будем называть горизонтальной проекцией точки А, а ортогональную проекцию А₂ точки А на плоскость П₂ - фронтальной проекцией точки А. Прямые АА₁ и АА₂, при помощи которых точка А проецируется на плоскости проекций (AА₁ ^ П₁, AА₂ ^ П₂), называются проецирующими прямыми (AА₁ – горизонтально проецирующая прямая, АА₂ – фронтально проецирующая прямая). Прямая пересечения плоскостей проекций называется осью проекций. Её обозначают буквой x.

Плоскость, перпендикулярную к плоскости проекций, называют проеци­рующей плоскостью (плоскость, перпендикулярная к плоскости П₁, называется горизонтально проецирующей плоскостью, а плоскость, перпендикулярная к плоскости П₂, – фронтально проецирующей плоскостью).

Плоскость АА₁А₂ проходит через прямую АА₁, перпендикулярную к плоскости П₁, в силу чего она перпендикулярна к плоскости П₁. Аналогично плоскость АА₁А₂ перпендикулярна плоскости П₂. Следовательно, дважды про­ецирующая плоскость АА₁А₂ перпендикулярна к оси проекций X.

Точку пересечения плоскости АА₁А₂ с осью проекций х как точку, при­надлежащую одновременно обеим плоскостям П₁ и П₂, обозначим А₁₂. Прямые A₁₂А₁ и А₁₂А₂, лежащие в плоскости АА₁А₂, перпендикулярной к оси проекций х, перпендикулярны к этой оси. Обратно, пусть А₁₂ - произвольная точка оси проекций х. Восставим из точки А₁₂ к оси два перпендикуляра: один в плоскости П₁, другой в плоскости П₂.

Рисунок 1.2.6 – Ортогональное проецирование точки

Тогда каждая пара точек А₁ и А₂, лежащих на этих перпендикулярах, оп­ределит в пространстве единственную точку А. Действительно, две пересекаю­щиеся прямые А₁₂А₁ и А₁₂А₂ определяют плоскость А₁А₁₂А₂, перпенди­кулярную к оси проекций х (так как А₁₂А₁ ^ х и А₁₂А₂ ^ х). Но плоскость, пер­пендикулярная к линии х пересечения двух плоскостей П1 и П₂, перпенди­кулярна к каждой из этих плоскостей, т.е. плоскость А₁А₁₂А₂ является проеци­рующей по отношению к обеим плоскостям проекций. Следовательно, перпен­дикуляры, восставленные в точках А₁ и А₂ соответственно к плоскостям П₁ и П₂, лежат в одной плоскости (в плоскости А₁ А₁₂А₂). Точка А их пересечения и является искомой точкой пространства, определяемой данной парой точек Итак, каждой точке А соответствует пара её проекций А₁ и А₂, лежащих вместе с данной точкой А в одной плоскости, перпендикулярной к обеим плос­костям проекций П₁ и П₂, а следовательно, и к линии х их пересечения; обрат­но, любые две точки А₁ Î П₁ и А₂ Î П₂, лежащие в одной плоскости, перпенди­кулярной к оси х, определяют в пространстве единственную точку А.

Расстояние А₁А точки А от горизонтальной плоскости проекций называ­ется высотой точки А, а её расстояние А₂А от фронтальной плоскости проекций – глубиной точки А.

Для получения плоского чертежа совмещаем плоскость проекций П₁ с плоскостью П₂ путем вращения плоскости П₁ вокруг оси X в направлении, ука­занном на рисунке 1.2.6 стрелками, так, чтобы передняя полуплоскость П₁ совмести­лась с нижней полуплоскостью П₂. В результате получим комплексный чертёж точки А (рисунок 1.2.7), состоящий из двух проекций А₁ и А₂ точки А. Обе проекции А₁ и А₂ лежат на одном перпендикуляре к оси проекций х, которую как прямую, принадлежащую одновременно обеим плоскостям проекций П₁ и П₂, будем обозначать на комплексном чертеже х₁₂. Два перпендикуляра А₁₂А₁ и А₁₂А₂ к оси х₁₂ имеют общую точку А₁₂. Прямая А₁А₂, соединяющая две проек­ции точки на комплексном чертеже, называется линией связи. Линия связи двух проекций точки перпендикулярна к оси проекций.

ПРИМЕЧАНИЕ: контуры плоскостей проекций на комплексном чертеже не показывают.

Рисунок 1.2.7 – Комплексный чертёж точки

Плоскости проекций разбивают всё пространство на четыре части, назы­ваемые квадрантами или четвертями. Принято нумеровать квадранты в порядке, указанном на рисунке 1.1.8, и называть их I, П, Ш, IV квадрантами.

 

 

Рисунок 1.2.8 – Квадранты пространства

 

Если точка лежит в I квадранте, то её горизонтальная проекция А₁, будет принадлежать передней полуплоскости П₁, а фронтальная проекция А₂ – верх­ней полуплоскости П₂. При совмещении плоскостей проекций горизонтальная проекция А₁ точки А, лежащей в I квадранте, окажется расположенной ниже оси x₁₂ в соответствии с рисунком 1.2.9.

В зависимости от положения натуральных (проецируемых) точек в раз­личных квадрантах пространства будем иметь соответствующее рас­положение их проекций на комплексном чертеже в соответствии с рисунком 1.2.9, так же как и обрат­но: по расположению проекций можно судить о том, в каком квадранте лежит натуральная точка.

 

Рисунок 1.2.9 – Комплексный чертёж точек, расположенных в разных квадрантах

Двухкартинный чертёж является метрически определённым чертежом. Однако, в силу трёхмерности пространственной фигуры её комплексный чертёж становится более ясным, когда, помимо двух основных проекций, дана ещё од­на проекция на третью плоскость. В качестве такой плоскости проекций чаще всего применяют профильную плоскость проекций П₃ (рис. 1.2.10).

П₃ ^ х, поэтому П₃ ^ П₁ и П₃ ^ П₂. Три плоскости проекций (П₁, П₂, П₃) об­разуют в пространстве прямоугольный трёхгранник, т.е. систему трёх взаимно перпендикулярных плоскостей. Ребра трёхгранника обозначим через х, y, z.

Пусть А – некоторая точка пространства. Для определения положения точки А относительно системы плоскостей (П₁, П₂, П₃) опустим из точки А пер­пендикуляры на плоскости проекций: AA_i ^ П_i (i=l, 2, 3). Основания этих пер-пендикуляров (точки А₁, А₂, А₃) и являются соответственно горизонтальной, фронтальной и профильной проекциями точки А в системе плоскостей проек­ций (П₁, П₂, П₃). Проецирующие плоскости AA₁A₂, AA₁A₃ и АА₂А₃ перпенди­кулярны соответственно к осям х, у, z. Обозначим точки пересечения этих плоскостей с осями через А₁₂, А₁₃, А₂₃. Как прямые A₁A₁₂ и A₁₂A₂ перпенди­кулярны к оси x, так и две другие пары прямых A₁A₁₃, A₁₃A₃ и А₂А₂₃, А₂₃А₃ должны быть перпендикулярны соответственно к осям y и z. Расстояние точки А от профильной плоскости проекций П₃ называется широтой точки А.

 

 

Рисунок 1.2.10 – Трёхкартинный чертёж точки

 

Итак, A₁A=A₁₂A₂=A₁₃A₃ – высота, А₂А=А_]2А₁=А₂₃A₃ – глубина, АзА=А₂₃A₂=A₁₃A₁ – ши­рота точки А.

При построении плоского чертежа плоскость П₂ считается неподвижной, а плоскости П₁ и П₃ совмещаются с ней путём вращения соответственно вокруг осей х и z в направлении, в соответствии с рисунком 1.2.10. После совмещения плоскости П₁ с фронтальной плоскостью П₂ отрезки А₁А₁₂ ^ x₁₂ и А₁₂А₂ ^ x₁₂ окажутся расположенными на одной прямой. Аналогично после совмещения плоскости П₃ с плоскостью П₂ отрезки А₂А₂₃ ^ z₂₃ и А₂₃А₃ ^ z₂₃ расположатся на линии связи А₂А₃ ^ z₂₃.

 

Рисунок 1.2.11 – Трёхпроекционный комплексный чертёж точки

 

В результате указанного совмещения плоскостей проекций получаем комплексный чертёж точки А в трёх ортогональных проекциях. При этом линии связи должны быть перпендикулярны к осям А₁А₂ ^ x₁₂, А₂А₃ ^ z₂₃, а отрезки А₁₂А₁ и А₂₃А₃ равны, так как А₁₂А₁₌А₂₃А₃=А₂А (рисунок 1.1.11) есть глубина точки А.

Рассмотрим квадрат А₁₃O₁₂₃А₃₁А₀. Диагональ этого квадрата является биссектрисой угла (Х₁₂Z_{23 ).} Следовательно, линия связи, соединяющая проекции А₁ и А₂, представляет собой ломаную линию с вершиной на биссектрисе К₁₂₃