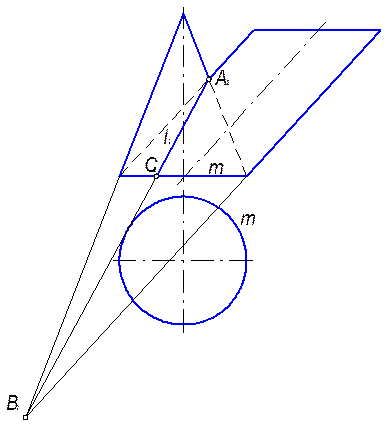Особые случаи пересечения поверхностей второго порядка

 

Поскольку поверхности второго порядка являются алгебраическими, то и линия их пересечения есть алгебраическая кривая. Так как порядок линии пересечения равен произведению порядков поверхностей, то эта линия – кривая четвёртого порядка. В ряде случаев кривая распадается на несколько линий более низких порядков. Для технических задач важно распадение на две кривые второго порядка, на две плоские кривые. Условия, при которых это возможно, выражены в следующих теоремах.

Теорема 1. Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются и ещё по одной кривой, которая тоже является плоской.

Рассмотрим пример (рисунок 1.3.57). Круговой конус и цилиндр второго порядка имеют общее круговое основание m (m₁, m₂). Значит, эти поверхности пересекаются по одной плоской кривой.

Вторую кривую пересечения найти легко, так как общая плоскость симметрии поверхностей параллельна плоскости проекций П₂, а поэтому искомая кривая на этой плоскости изобразится одной прямой. Для её построения достаточно двух точек – А (А₂) и В (В₂). Следовательно, вторая часть линии пересечения будет частью эллипса АВ (А₂В₂); по её фронтальной проекции легко достраивать и горизонтальную проекцию.

 

Рисунок 1.3.57 – Особый случай пересечения поверхностей второго порядка

 

Теорема 2 (о двойном прикосновении). Если две поверхности второго порядка имеют касание в двух точках, то линия их пересечения распадается на две плоские кривые (второго порядка), плоскости которых проходят через прямую, соединяющую точки касания.

Пример, иллюстрирующий эту теорему, приведён на рисунке 1.3.58.

 

Рисунок 1.3.58 – Особый случай пересечения поверхностей второго порядка

 

Пересекаются круговой и эллиптический цилиндры, соприкасающиеся в точках А (А₁, А₂) и В (В₁, В₂). Плоские кривые пересечения изображаются на фронтальной плоскости проекций прямыми D₂E₂ и C₂F₂, так как эти кривые лежат в плоскостях, проходящих через прямую АВ (А₁В₁, А₂В₂) и поэтому фронтально проецирующих.

Теорема Г. Монжа. Если две поверхности второго порядка описаны около третьей или вписаны в неё, то они пересекаются по двум плоским кривым. Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания.

Рисунок 1.3.59 – Пересечение поверхностей, описанных около сферы

 

Рассмотрим пример (рисунок 1.3.59).

Пересекаются круговые конус и цилиндр, описанные около сферы. Линиями пересечения будут два эллипса, изображающиеся во фронтальной проекции прямыми А₂В₂ и С₂D₂.

 

Рисунок 1.3.60 – Пересечение поверхностей, вписанных в сферу

 

На рисунке 1.3.60 показано пересечение сжатых эллипсоидов вращения, вписанных в общую сферу.

Теорема Г. Монжа представляет частный случай теоремы о двойном прикосновении.

1.4 Преобразование комплексного чертежа

Решение многих пространственных задач (позиционных и метрических) на комплексном чертеже часто усложняется из-за того, что заданные геометрические объекты расположены произвольно относительно плоскостей проекций и, следовательно, проецируются на эти плоскости в искажённом виде. Поэтому для более простого решения задач используют такое преобразование комплексного чертежа, которое переводило бы интересующие нас объекты из общего положения относительно плоскостей проекций в частное.

Задание на чертеже прямых и плоскостей частного положения значительно упрощает решение задач и делает его выполнимым при помощи простых замеров или простейших графических построений.

Чертёж можно преобразовать, изменяя относительное расположение пространственных объектов и плоскостей проекций с целью перехода объектов от общего положения к частному. Этого можно достигнуть двумя способами:

1) заменой данной системы плоскостей проекций новой системой так, чтобы неподвижный в пространстве объект оказался в каком-либо частном положении относительно новой системы. Это способ замены плоскостей проекций;

2) перемещением объекта в пространстве так, чтобы он оказался в частном положении относительно неизменной системы плоскостей проекций. Это способ плоско параллельного перемещения и его разновидность – способ вращения вокруг проецирующей прямой.