
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение поверхностей вращенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Линией пересечения поверхностей является плоская или пространственная кривая, состоящая из: - одного замкнутого контура, если одно геометрическое тело частично врезается в поверхность другого; - распадается на несколько линий, если поверхность одного тела полностью пронизывает поверхность другого. Рассмотрим особые случаи пересечения поверхностей вращения. Цилиндрические, конические поверхности и однополосный гиперболоид вращения относятся к линейчатым поверхностям вращения второго порядка. Сфера, эллипсоид вращения, параболоид вращения и двухполосный гиперболоид вращения – нелинейчатые поверхностям второго порядка. Поверхность второго порядка – множество точек пространства, декартовые координаты которых соответствуют алгебраическому уравнению второй степени.
Из аналитической геометрии известно, что порядок линии пересечения поверхностей равен произведению порядков поверхностей. Поэтому в общем случае две поверхности второго порядка (квадрики) пересекаются по пространственной линии четвертого порядка (биквадратной кривой), которая иногда распадается на несколько линий. В некоторых частных случаях линия пересечения распадается на две плоские кривые второго порядка. Условия, при которых это возможно, определены в следующих теоремах. Зная их, можно быстрее и точнее построить линию пересечения поверхностей.
Рис. 6.19 Теорема 1: Если две квадрики пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются.
Например, линия пересечения сферы и эллиптического цилиндра с круговым основанием распадается на две коники – окружности (q, q ¢). Теорема 2: Если две квадрики имеют касание в двух точках, то линия их пересечения распадается на две коники, плоскости которых проходят через отрезок прямой, соединяющей эти точки.
Рис. 6.20
Поверхности прямого кругового цилиндра и эллиптического цилиндра с круговым основанием имеют две общие точки касания (А, В). Следовательно, по Т2 они пересекаются по двум коникам – окружности (q) и эллипсу (q ¢), плоскости которых пересекаются по прямой АВ. Теорема 3: Две соосные поверхности вращения пересекаются по окружностям-параллелям, число которых равно числу точек пересечения главных полумеридианов поверхностей.
Рис. 6.21
Соосными называются поверхности, имеющие общую ось вращения. Так как плоскость сечения перпендикулярна оси вращения i, линия сечения (окружность) проецируется: - в окружность на плоскость, перпендикулярную оси i; - в отрезок прямой – на плоскость, параллельную оси i; - в эллипс – на любую другую плоскость.
Эти особенности соосных поверхностей вращения позволяют использовать их, в частности сферу, в качестве посредников при построении линии пересечения поверхностей вращения. Любая поверхность вращения, ось которой проходит через центр сферы, соосна с ней и, следовательно, пересекает ее по окружности. Теорема 4 (Теорема Монжа): Если две поверхности второго порядка (квадрики) описаны вокруг третьей квадрики, то они пересекаются по двум плоским кривым второго порядка (коникам).
Рис. 6.22
В соответствии с этой теоремой, линии пересечения поверхностей, описанных около сферы, будут плоскими кривыми – эллипсами. Построение линии пересечения поверхностей вращения в общем случае ведется с помощью дополнительных секущих поверхностей, в качестве которых могут быть использованы плоскости или сферы. Секущие поверхности выбираются таким образом, чтобы с заданными поверхностями они пересекались по линиям, легко определяемым на КЧ. Чтобы построить линию пересечения поверхностей на КЧ, необходимо: 1. Ввести ряд вспомогательных плоскостей или сфер, пересекающих обе заданные поверхности. 2. Построить линию пересечения каждой заданной поверхности со вспомогательной. 3. В месте пересечения построенных таким образом линий определить точки искомой линии взаимного пересечения. 4. Соединить полученные точки пересечения между собой с учетом видимости линии сечения. Способ нахождения линии пересечения с помощью дополнительных плоскостей называется способом секущих плоскостей, а нахождение линии сечения с помощью дополнительных сфер – способом секущих сфер. Каким бы способом не производилось нахождение линии пересечения, ее построение начинается с определения характерных точек сечения, а затем определяются промежуточные точки, необходимые для точности построения линии пересечения. К характерным точкам линии пересечения относятся: 1. точки, проекции которых лежат на проекциях контурных образующих (очерках) заданных поверхностей; 2. «крайние» точки – правые и левые, наивысшие и наинизшие, ближайшие и наиболее удаленные. Способ секущих плоскостей Обычно в качестве секущих плоскостей используются плоскости уровня, т.к. линии пересечения их с заданными поверхностями проецируются на плоскость проекций без искажения. Также в некоторых случаях используются и проецирующие плоскости. Этот способ применяют тогда, когда дополнительные плоскости рассекают заданные поверхности по окружностям-параллелям или прямым-образующим. Пример: Построить линию пересечения кругового конуса и сферы.
Рис. 6.23 Конус и сфера имеют общую плоскость симметрии Обе поверхности содержат семейство параллелей, параллельных горизонтальной плоскости проекций, поэтому остальные точки линии сечения необходимо находить с помощью горизонтальных плоскостей уровня. Точки C и D, лежащие на границе видимости, находятся с помощью плоскости
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

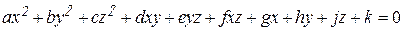 .
.


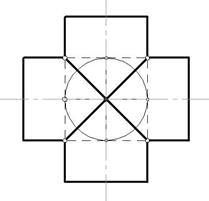

 , параллельную фронтальной плоскости проекций, с помощью которой находятся высшая и низшая точки линии сечения А и В. Эта плоскость пересекает конус по очерковым образующим l, а сферу – по главному меридиану m.
, параллельную фронтальной плоскости проекций, с помощью которой находятся высшая и низшая точки линии сечения А и В. Эта плоскость пересекает конус по очерковым образующим l, а сферу – по главному меридиану m. , проходящей через экватор сферы. Эта плоскость, в свою очередь, пересекает конус по параллели n радиуса r.
, проходящей через экватор сферы. Эта плоскость, в свою очередь, пересекает конус по параллели n радиуса r.


