Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Пересечение поверхности с плоскостьюСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вопросы:
1. В чём сущность алгоритма построения сечения поверхности плоскостью? 2. Какие линии получаются в сечении плоскостью цилиндрической поверхности вращения? 3. Какие линии получаются в сечении плоскостью конической поверхности вращения? 4. Какие точки линии пересечения относятся к опорным? Задачи: 19. Построить проекции сечения данной поверхности проецирующей плоскостью Σ.
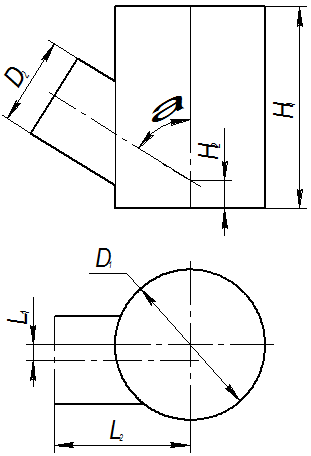
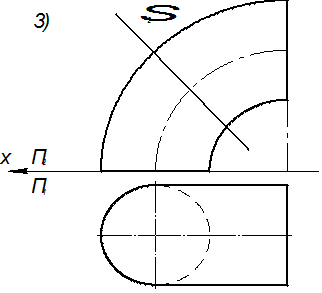
Пример 4. Дан тор и плоскость Σ Решение. Так как искомое сечение принадлежит плоскости Σ, а плоскость занимает фронтально проецирующее положение, то фронтальная проекция сечения будет находиться на следе этой плоскости. Горизонтальную проекцию сечения определяем из условия принадлежности линии поверхности. Тогда последовательность построений будет следующей: а) определяем опорные точки сечения – 1, 2, 3, 4, 5, 6, 7, 8 (точки 7 и 8 удалены на кратчайшее расстояние от оси тора, а остальные точки принадлежат очеркам поверхности); б) определяем промежуточные точки – 9, 10, 11, 12, 13, 14, 15, 16 (для их построения на торе проведены параллели); в) полученные точки соединяем с учётом видимости.
Рис. 4
Тема 8. Пересечение прямой линии с поверхностью Вопросы:
1. В чём сущность алгоритма построения точек пересечения прямой с поверхностью? 2. Как использовать вспомогательные секущие плоскости при построении точек пересечения прямой общего положения с заданными поверхностями? 3. Как на чертеже определяется видимость проекций прямой, пересекающейся с поверхностью? Задачи: 20. Построить точки пересечения прямой с заданной поверхностью. Установить видимость проекций прямой.
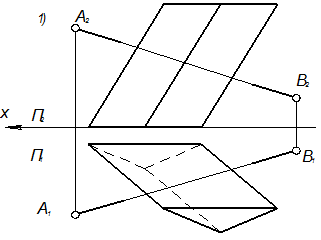
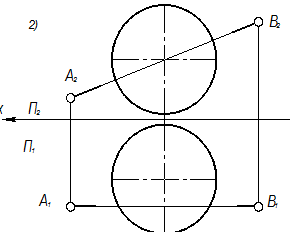
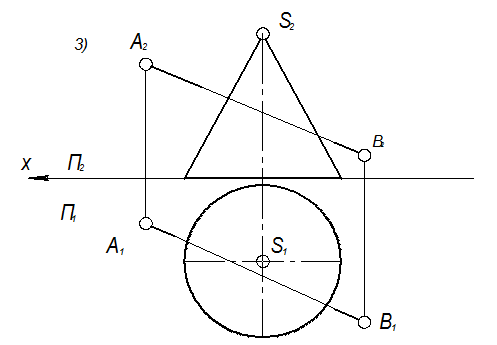
Пример 5. Дан тор и прямая АВ. Построить точки пересечения тора и прямой (рис. 5). Последовательность решения: а) заключаем прямую АВ в плоскость Σ б) строим сечение l(l1, l2) тора этой плоскостью (см. пример 4); в) определяем точки пересечения прямой АВ и построенного сечения l, М=АВ г) определяем видимость проекций прямой.
Рис.5 Тема 9. Взаимное пересечение поверхностей Метод секущих плоскостей Вопросы:
1. В чём сущность алгоритма построения линии пересечения двух поверхностей методом секущих плоскостей? 2. Каким условиям должны удовлетворять плоскости-посредники? 3. Какие точки линии пересечения являются опорными? 4. Как устанавливается видимость проекций линии пересечения поверхностей?
Исходные данные к заданию “Пересечение поверхностей”
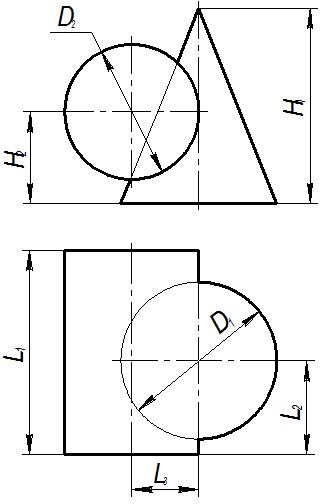
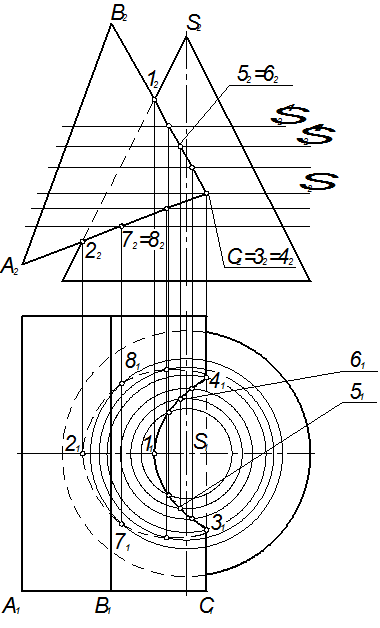
Пример 7. Даны коническая поверхность вращения и трёхгранная призма. Построить линию их пересечения (рис. 6). Последовательность решения: 1. Выбираем плоскости-посредники так, чтобы в пересечении их с заданными поверхностями получались графически простые линии – прямые или окружности. В рассматриваемом примере такие плоскости параллельны горизонтальной плоскости проекций. Они пересекают конус по окружности, а призму – по прямым. 2. Определяем опорные точки линии пересечения – точки 1, 2, 3, 4. 3. Строим промежуточные точки линии пересечения, изменяя положения плоскостей-посредников. 4. Соединяем проекции линии пересечения с учётом видимости - относительно П1 невидимым будет участок кривой, расположенный на нижней (невидимой) грани призмы.
Рис. 6 Тема 10. Взаимное пересечение поверхностей
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

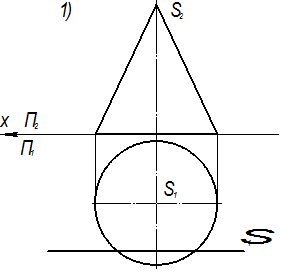
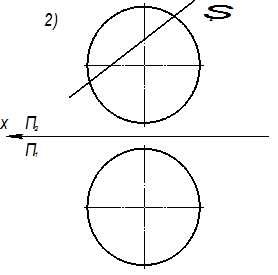
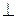 П2. Построить сечение тора
П2. Построить сечение тора 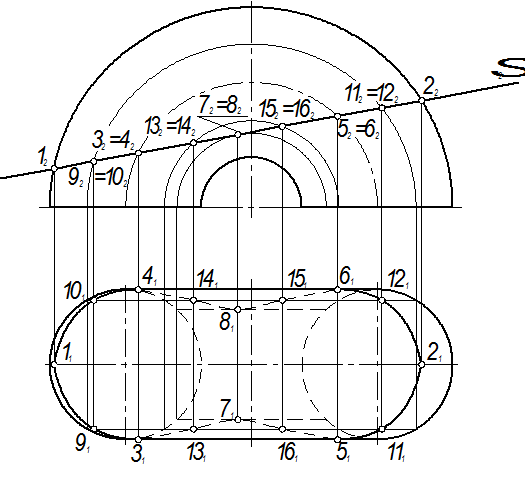
 l, N=AB
l, N=AB 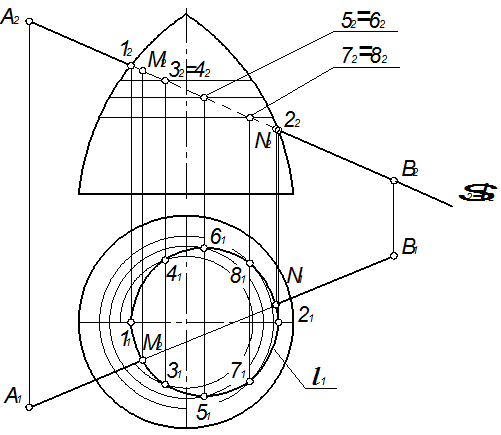
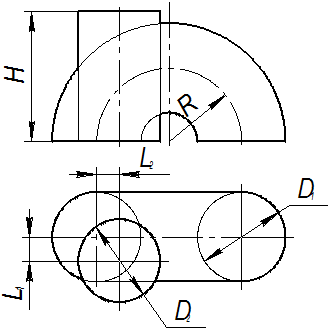
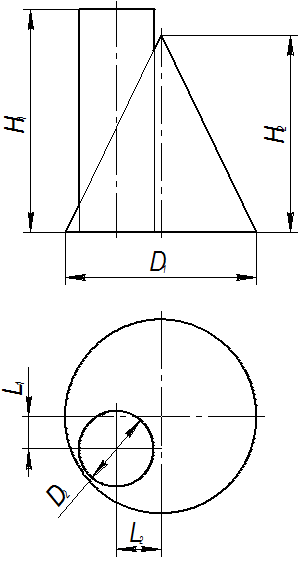 Таблица 3
Таблица 3