Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Изображение точек на комплексном чертеже.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ ИНЖЕНЕРНАЯ ГРАФИКА
Рабочая тетрадь для решения задач
Омск 2007 Составители: Кошелева Л.И., Притыкин Ф.Н., Кузнецов С.А.
Рецензенты: Иванов В.В., канд. техн. наук, доцент кафедры «Детали машин и инженерная графика», ОмГАУ
Рабочая тетрадь для решения задач по дисциплинам «Начертательная геометрия» и «Инженерная графика» для студентов заочной формы обучения / Кошелева Л.И., Притыкин Ф.Н.,
Сборник задач составлен в соответствии с государственным образовательным стандартом профессионального высшего образования дисциплины «Начертательная геометрия и инженерная графика». Предназначен для студентов заочной формы обучения.
Печатается по решению редакционно-издательского совета Омского государственного университета.
© Кошелева Л.И., Притыкин Ф.Н., Кузнецов С.А., 2007 © Омский государственный технический университет, 2007 ВВЕДЕНИЕ
Рабочая тетрадь предназначена для студентов первого курса заочной формы обучения, изучающих дисциплины «Начертательная геометрия» и «Инженерная графика». Самостоятельная практическая работа студентов по указанным дисциплинам включает решение задач в данной рабочей тетради и выполнение графических работ на чертежной бумаге (ватмане). Графические работы следует выполнять в соответствии со стандартами, устанавливающими правила оформления чертежей. В рабочей тетради приведены условия задач, показаны примеры их выполнения по основным разделам дисциплины. Перед решением задач рекомендуется изучить теоретический материал, отраженный в перечне вопросов, приведённых в начале каждого раздела. Если указанные вопросы вызывают затруднения, то необходимо обратится к учебному пособию с целью изучения соответствующих разделов дисциплин. Графические построения при решении задач в данной рабочей тетради выполняются карандашом с использованием чертежных инструментов. Для большей наглядности при построении изображений, рекомендуется использовать цветные карандаши. Точки и линии должны быть обозначены буквами или цифрами (размер шрифта № 5).
Принятые обозначения
1. Точки в пространстве – прописными буквами латинского алфавита – А, В, С,… или цифрами 1, 2, 3,… 2. Линии – строчными буквами латинского алфавита – а, b, c,… 3. Плоскости – строчными буквами греческого алфавита – α,β,γ,δ,ε,…; плоскости проекций – П1, П2, П3, … 4. Проекции точек, линий и плоскостей обозначают теми же буквами, только с индексами: например, проекции на плоскости П1 – А1, В1, a1, b1, α1; на плоскости П2 – А2, В2, a2, b2, α2. Используются = – совпадение, равенство, результат действия;
|| – параллельность;
Î – принадлежность элемента множеству; Ì – принадлежность подмножества множеству;
Тема 1. Изображение точек на комплексном чертеже.
Вопросы:
1. Что представляет собой метод ортогональных проекций? 2. Что называют координатами точки? 3. Что такое комплексный чертеж точки? 4. Назовите законы проекционной связи. 5. Какие точки называются конкурирующими?
Задачи:
1. Построить точки А (40,20,30), В (40,30,0), С (0,0,30) и D (0,10,20) на комплексном чертеже. Координаты точек заданы в миллиметрах.
2. Точки А, В и С принадлежат плоскостям проекций. Построить недостающие проекции этих точек и указать в какой плоскости каждая из них располагается.
Тема 6. Поверхности. Принадлежность точек и линий поверхностям Вопросы:
1. Что является определителем кинематической поверхности? 2. Какие поверхности называются линейчатыми? 3. Какая поверхность называется циклической? 4. Что является определителем поверхности вращения? 5. Что такое очерк и контур поверхности? 6. Сформулируйте условия принадлежности точки и линии к поверхности. Задачи:
18. Построить недостающие проекции точек, лежащих на видимой части поверхностей: а) конической поверхности вращения; б) сферы; в) тора.
Тема 9. Взаимное пересечение поверхностей Метод секущих плоскостей Вопросы:
1. В чём сущность алгоритма построения линии пересечения двух поверхностей методом секущих плоскостей? 2. Каким условиям должны удовлетворять плоскости-посредники? 3. Какие точки линии пересечения являются опорными? 4. Как устанавливается видимость проекций линии пересечения поверхностей?
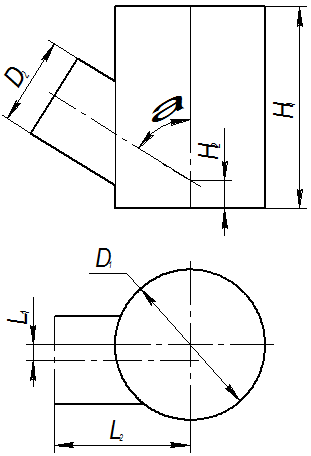
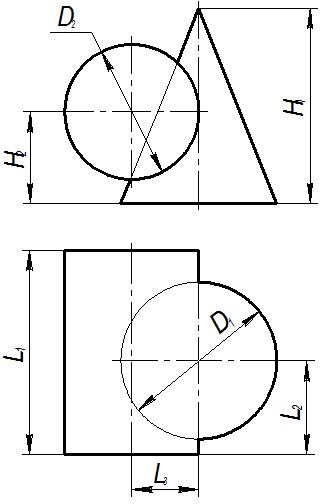
Исходные данные к заданию “Пересечение поверхностей”
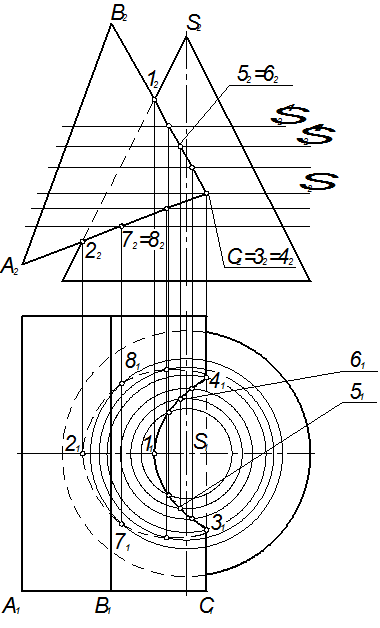
Пример 7. Даны коническая поверхность вращения и трёхгранная призма. Построить линию их пересечения (рис. 6). Последовательность решения: 1. Выбираем плоскости-посредники так, чтобы в пересечении их с заданными поверхностями получались графически простые линии – прямые или окружности. В рассматриваемом примере такие плоскости параллельны горизонтальной плоскости проекций. Они пересекают конус по окружности, а призму – по прямым. 2. Определяем опорные точки линии пересечения – точки 1, 2, 3, 4. 3. Строим промежуточные точки линии пересечения, изменяя положения плоскостей-посредников. 4. Соединяем проекции линии пересечения с учётом видимости - относительно П1 невидимым будет участок кривой, расположенный на нижней (невидимой) грани призмы.
Рис. 6 Библиографический список 1. Четверухин Н.Ф., Левицкий В.С. Начертательная геометрия. / Н.Ф.Четверухин, В.С.Левицкий – М.: Высш. шк., 1972 – 310 с. 2. Арустамов Х.А. Сборник задач по начертательной геометрии. – М.: Машиностроение, 1971 – 375 с. 3. Бубенников А.В., Громов М.Я. Начертательная геометрия. / А.В.Бубенников, М.Я.Громов – М.: Высш. шк., 1973 – 210 с. 4. Кошелева Л.И., Леонова Л.М., Ляшков А.А. Задания по инженерной графике. Методические указания. Омск, 2001 – 54 с. 5. ГОСТ 2.301-68. Форматы. – М.: ГОССТАНДАРТ, 1991. – 236 с. 6. ГОСТ 2.303-68. Линии. – М.: ГОССТАНДАРТ, 1991. – 236 с. 7. Ляшков А.А. Начертательная геометрия: Конспект
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ ИНЖЕНЕРНАЯ ГРАФИКА
Рабочая тетрадь для решения задач
Омск 2007 Составители: Кошелева Л.И., Притыкин Ф.Н., Кузнецов С.А.
Рецензенты: Иванов В.В., канд. техн. наук, доцент кафедры «Детали машин и инженерная графика», ОмГАУ
Рабочая тетрадь для решения задач по дисциплинам «Начертательная геометрия» и «Инженерная графика» для студентов заочной формы обучения / Кошелева Л.И., Притыкин Ф.Н.,
Сборник задач составлен в соответствии с государственным образовательным стандартом профессионального высшего образования дисциплины «Начертательная геометрия и инженерная графика». Предназначен для студентов заочной формы обучения.
Печатается по решению редакционно-издательского совета Омского государственного университета.
© Кошелева Л.И., Притыкин Ф.Н., Кузнецов С.А., 2007 © Омский государственный технический университет, 2007 ВВЕДЕНИЕ
Рабочая тетрадь предназначена для студентов первого курса заочной формы обучения, изучающих дисциплины «Начертательная геометрия» и «Инженерная графика». Самостоятельная практическая работа студентов по указанным дисциплинам включает решение задач в данной рабочей тетради и выполнение графических работ на чертежной бумаге (ватмане). Графические работы следует выполнять в соответствии со стандартами, устанавливающими правила оформления чертежей. В рабочей тетради приведены условия задач, показаны примеры их выполнения по основным разделам дисциплины. Перед решением задач рекомендуется изучить теоретический материал, отраженный в перечне вопросов, приведённых в начале каждого раздела. Если указанные вопросы вызывают затруднения, то необходимо обратится к учебному пособию с целью изучения соответствующих разделов дисциплин. Графические построения при решении задач в данной рабочей тетради выполняются карандашом с использованием чертежных инструментов. Для большей наглядности при построении изображений, рекомендуется использовать цветные карандаши. Точки и линии должны быть обозначены буквами или цифрами (размер шрифта № 5).
Принятые обозначения
1. Точки в пространстве – прописными буквами латинского алфавита – А, В, С,… или цифрами 1, 2, 3,… 2. Линии – строчными буквами латинского алфавита – а, b, c,… 3. Плоскости – строчными буквами греческого алфавита – α,β,γ,δ,ε,…; плоскости проекций – П1, П2, П3, … 4. Проекции точек, линий и плоскостей обозначают теми же буквами, только с индексами: например, проекции на плоскости П1 – А1, В1, a1, b1, α1; на плоскости П2 – А2, В2, a2, b2, α2. Используются = – совпадение, равенство, результат действия;
|| – параллельность;
Î – принадлежность элемента множеству; Ì – принадлежность подмножества множеству;
Тема 1. Изображение точек на комплексном чертеже.
Вопросы:
1. Что представляет собой метод ортогональных проекций? 2. Что называют координатами точки? 3. Что такое комплексный чертеж точки? 4. Назовите законы проекционной связи. 5. Какие точки называются конкурирующими?
Задачи:
1. Построить точки А (40,20,30), В (40,30,0), С (0,0,30) и D (0,10,20) на комплексном чертеже. Координаты точек заданы в миллиметрах.
2. Точки А, В и С принадлежат плоскостям проекций. Построить недостающие проекции этих точек и указать в какой плоскости каждая из них располагается.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 814; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.161.178 (0.007 с.) |

 – скрещивание прямых;
– скрещивание прямых; – перпендикулярность;
– перпендикулярность; – объединение, например, А
– объединение, например, А  – пересечение, например, a
– пересечение, например, a 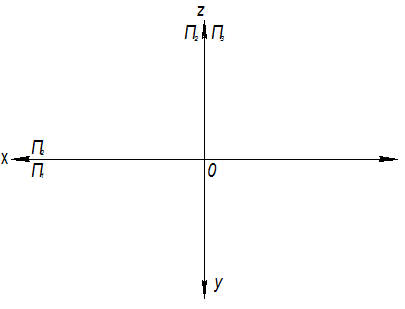


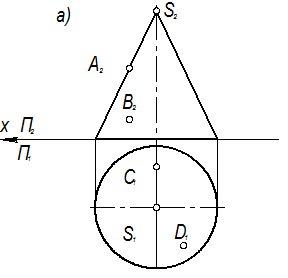


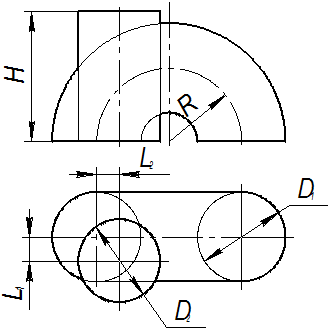
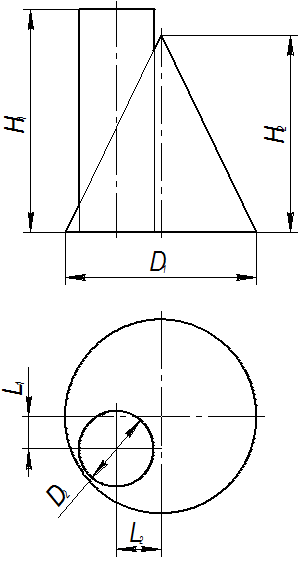 Таблица 3
Таблица 3