
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение поверхности вращения плоскостьюСодержание книги
Поиск на нашем сайте Форма сечения поверхности вращения плоскостью зависит от угла наклона секущей плоскости к оси вращения поверхности. Если секущая плоскость: 1) перпендикулярна оси вращения, сечение – окружность; 2) наклонена к оси и пересекает все образующие – эллипс; 3) параллельна одной образующей – парабола; 4) параллельна двум образующим – гипербола; 5) проходит через вершину – две пересекающиеся прямые; 6) касается поверхности – прямая. Вся совокупность этих линий может быть получена при пересечении конуса плоскостью. Поэтому их называют коническими сечениями, или кониками.
Рис. 6.14 Для построения линии пересечения необходимо найти общие точки поверхности и заданной плоскости. Для определения этих точек необходимо ввести дополнительные секущие плоскости, которые дают наиболее простые линии сечения – окружности или ломаные прямые. Построение линии сечения начинают с нахождения характерных точек сечения, к которым относятся: 1) высшая и низшая точки; 2) крайняя левая и крайняя правая точки, в которых проекции линии сечения касаются очерковых образующих (точки, лежащие на границе видимости); 3) ближайшая и наиболее удаленная точки сечения. Пример: Определить линию сечения конуса плоскостью общего положения Q(hÇf). Построить развертку нижней отсеченной поверхности конуса. Анализ формы линии пересечения Заданная плоскость пересекает только боковую поверхность конуса, следовательно, линией сечения q является эллипс. Характерные точки линии пересечения: 1) Высшая и низшая точки сечения (А, В) определяют большую ось эллипса и лежат на линии наибольшего наклона плоскости
О – центр эллипса
2) Малая ось эллипса (С, D) перпендикулярна к линии наибольшего наклона (большой оси), т.е. лежит на горизонтали плоскости
3) Точки границы видимости (E, F) сечения на
Рис. 6.15
Развертка
Полная развертка боковой поверхности конуса представляет собой угол кругового сектора. Ее можно построить двумя способами:
1. Нахождение угла кругового сектора.
Рис. 6.16
где d – диаметр окружности основания конуса, l – длина образующей.
2. Способ малых хорд. Графическое построение величины Разрывать отсеченную боковую поверхность следует по наиболее короткой или длинной образующей, так чтобы развертка представляла собой симметричную фигуру и была единым целым.
Рис. 6.17 Пересечение поверхностей Пересечение многогранников Многогранники пересекаются по замкнутым пространственным ломаным линиям, которые могут быть найдены следующим образом: 1. Способ ребер. Находятся точки пересечения ребер одного многогранника с гранями другого. 2. Способ граней. Определяются отрезки прямых, по которым грани одного многогранника пересекаются с гранями другого. Пример: Построить линию пересечения двух трехгранных призм, одна из которых проецирующая. В результате пересечения заданных многогранников получается ломаная пространственная линии. Она соединяет соответствующие точки пересечения ребер одного многогранника с гранями другого. Так как одна из призм проецирующая относительно горизонтальной плоскости проекций, горизонтальная проекция линии пересечения совпадает с горизонтальным очерком этой призмы. Искомые точки сечения можно получить, решая задачу на пересечение прямой (ребра) с плоскостью (гранью).
Для построения точек пересечения ребра b с гранями призмы, используется горизонтально-проецирующая плоскость
Рис. 6.18 Для определения видимости линии сечения строится диаграмма, на которой схематично в произвольных размерах изображаются грани заданных призм. Знаками ²+² и ²-² отмечается видимость граней многогранников. На соответствующих гранях и ребрах наносятся точки сечения, и соединяют их с учетом видимости. Видимыми считаются те звенья линии пересечения, которые лежат на видимых гранях обоих многогранников. Лекция 11
|
||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |


 к плоскости основания конуса. Эти точки определяются с помощью дополнительной плоскости
к плоскости основания конуса. Эти точки определяются с помощью дополнительной плоскости  .
.

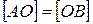
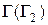 .
.

 лежат в плоскости
лежат в плоскости  , делящей конус на видимую и невидимую части по отношению к фронтальной плоскости проекций.
, делящей конус на видимую и невидимую части по отношению к фронтальной плоскости проекций.




 осуществляется способом малых хорд, при котором окружность основания конуса делится на 8 или 12 равных частей и полученная длина дуги приравнивается ее хорде.
осуществляется способом малых хорд, при котором окружность основания конуса делится на 8 или 12 равных частей и полученная длина дуги приравнивается ее хорде.
 ,
,  .
. ,
,  .
. .
. .
.



