
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства параллельного проецированияСодержание книги
Поиск на нашем сайте
При проецировании на плоскость проекций формы и размеры некоторых геометрических элементов могут искажаться. Однако существуют некоторые их свойства, которые всегда остаются неизменными (инвариантными). 1. Проекция точки есть точка. Это очевидно из самого определения проекции как точки пересечения проецирующего луча с плоскостью проекций. Следует помнить, что любой точке пространства соответствует только одна проекция на плоскости. Обратная формулировка этого свойства неверна, т.к. каждой проекции точки может соответствовать бесчисленное множество точек в пространстве. Это значит, что одна проекция точки не определяет ее положение в пространстве. 2. Проекцией прямой в общем случае является прямая. Все проецирующие лучи, проходящие через прямую, заданную отрезком АВ, образуют проецирующую плоскость АВВ¢А¢, которая пересекает плоскость проекций
Рис. 1.3
3. Прямая может быть проекцией не только прямой, но и любой кривой линии, если эта кривая находится в плоскости, перпендикулярной плоскости проекций (рис.1.3а). 4. Проекцией прямой, параллельной направлению проецирования, является точка. Она называется вырожденной проекцией прямой (рис. 1.3б).
5. а) Если отрезок параллелен плоскости проекций, то он проецируется на нее в натуральную величину.
б) В противном случае, при прямоугольном параллельном проецировании он имеет проекцию меньшую истиной величины.
Рис. 1.4
Рис. 1.5
6. Если точка принадлежит прямой, то проекция этой точки лежит на проекции этой прямой.
7. Если точка, лежащая на прямой, делит ее на отрезки в каком-либо отношении, то проекция этой точки поделит проекцию этой прямой в том же отношении.
8. Если прямые пересекаются, то их проекции тоже пересекаются. Причем проекция точки пересечения прямых является точкой пересечения проекций.
Рис. 1.6
Точка N одновременно принадлежит прямым (A-B) и (C-D). По шестому инвариантному свойству проекция этой точки должна принадлежать проекциям этих прямых, а следовательно, быть точкой пересечения проекций. 9. Проекции параллельных прямых параллельны между собой.
Плоскости Q и S, проходящие через две параллельные прямые, параллельны, т.к. две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым второй плоскости.
Параллельные плоскости пересекаются с третьей плоскостью
Рис. 1.7
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.86.209 (0.008 с.) |

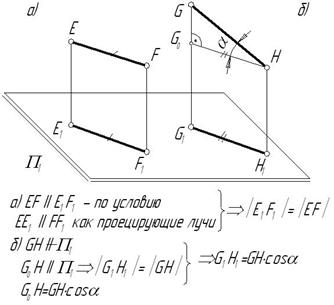
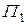 по прямой
по прямой  (рис. 1.3 а). Исходя из этого справедливо и следующее утверждение.
(рис. 1.3 а). Исходя из этого справедливо и следующее утверждение.




 .
.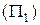 по параллельным прямым, следовательно,
по параллельным прямым, следовательно,  .
.



