Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение поверхности многогранника плоскостьюСодержание книги
Поиск на нашем сайте
Плоская фигура, получаемая в результате пересечения какой-либо поверхности плоскостью, называется сечением. Сечением многогранника является многоугольник, его обычно строят с помощью вспомогательных секущих плоскостей. Построение линии пересечения поверхности с плоскостью начинают с нахождения особых (опорных) точек. Для многогранника это точки пересечения ребер и сторон его основания с заданной плоскостью (если построение ведется «способом ребер») или линии пересечения граней и основания многогранника с плоскостью (если построение ведется «способом граней»). Пример: Построить линию пересечения трехгранной пирамиды SABC плоскостью общего положения Основание пирамиды принадлежит горизонтальной плоскости проекций, его горизонтальная проекция является натуральной величиной. Плоскость задана таким образом, что пересекает только боковую поверхность пирамиды. Следовательно, сечение будет иметь треугольную форму. Т.к. горизонталь плоскости h проходит через одну из вершин основания, то одна из точек сечения известна – точка C. Остальные точки сечения можно найти с помощью дополнительных секущих плоскостей Для улучшения наглядности изображения необходимо показать видимость: 1) сечения относительно поверхности многогранника и выделить его цветным карандашом; 2) поверхности относительно заданной плоскости; 3) геометрических элементов, которыми задана плоскость, относительно поверхности многогранника. Натуральная величина сечения определяется вращением вокруг линии уровня, другие необходимые для построения развертки натуральные величины в данной задаче определены методом прямоугольного треугольника.
Рис. 6.9 Построение развертки: 1. Методом прямоугольного треугольника находятся длины ребер пирамиды. Т.к. разность высот от концов отрезка до горизонтальной плоскости проекций P1 у всех трех ребер одна и равна высоте пирамиды, катет прямоугольного треугольника, равный этой величине, целесообразней начертить в стороне от изображения, правее фронтальной проекции пирамиды. Второй катет равен длинам горизонтальных проекций ребер. Для определения натуральной величины отрезков AK и BN необходимо провести горизонтальные вспомогательные линии от проекций точек К и N до пересечения с соответствующими гипотенузами прямоугольных треугольников.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.116 (0.008 с.) |

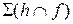 . Построить развертку нижней отсеченной части пирамиды.
. Построить развертку нижней отсеченной части пирамиды. и
и  , проходящих через ребра SA и SB.
, проходящих через ребра SA и SB.