
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые позиционные задачи пересечения многогранника с прямой и плоскостьюСодержание книги
Похожие статьи вашей тематики
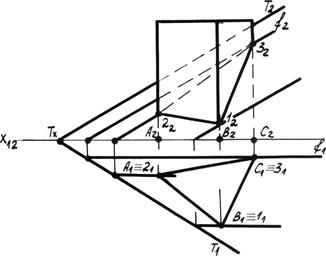
Поиск на нашем сайте Плоскость пересекает многогранную поверхность по плоской замкнутой ломаной линии, называемой фигурой сечения. Вершины и стороны фигуры сечения определяются пересечением заданной плоскости соответственно с рёбрами и гранями многоугольника. То есть многократно решается задача или на пересечение двух плоскостей (граней многогранника с секущей плоскостью), или на пересечение прямой с плоскостью (рёбер многогранника с секущей плоскостью). Это уже известные задачи. Задача: Дана треугольная наклонная пирамида и секущая фронтально проецирующая плоскость å (рис. 6.1). Определить проекции фигуры сечения.
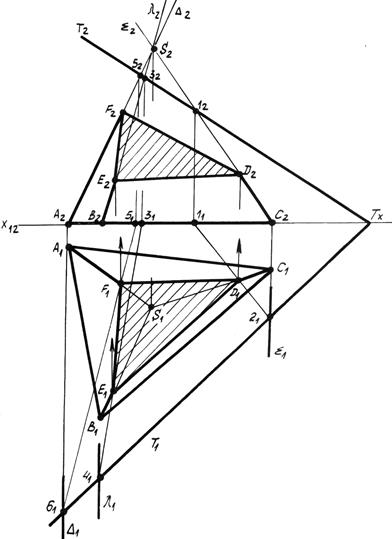
Решение: Так как секущая плоскость является фронтально проецирующей, то фронтальная проекция фигуры сечения (122232) совпадет со следом плоскости å2. Фигура сечения является треугольником и определяется на пересечении следа плоскости с соответствующими ребрами пирамиды. По линиям связи определяем горизонтальные проекции вершин треугольника (112131) на соответствующих ребрах пирамиды. Далее определяется видимость звеньев линии сечения в зависимости от видимости граней пирамиды на горизонтальной проекции. Задача: Дана прямая треугольная призма и секущая плоскость общего положения Т (рис. 6.2). Определить проекции фигуры сечения.
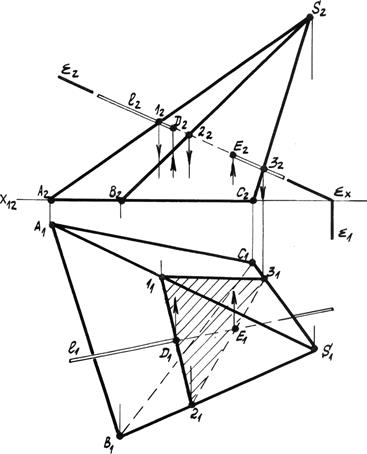
Решение: Так как боковые грани призмы являются горизонтально проецирующими плоскостями, то горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией призмы (А 1 В 1 С 1) º (112131). Решение задачи сводится к определению второй проекции точек сечения, принадлежащих и плоскости Т и призме. Для этого воспользуемся фронталями плоскости ¦, проведенными через соответствующие точки 11 º В 1, 21 º А 1, 31 º С 1. Фронтальную проекцию фигуры сечения (122232) определяем на пересечении фронтальных проекций фронталей с соответствующими рёбрами призмы. Определяем видимость звеньев линии сечения. Задача: Дана прямоугольная пирамида и секущая плоскость общего положения Т (рис. 6.3). Определить проекции фигуры сечения.
Решение: Ребра и грани пирамиды являются геометрическими объектами общего положения. Определим точки фигуры пересечения, решая несколько раз задачу на пересечение прямой с плоскостью (ребра пирамиды с секущей плоскостью). Для этого заключаем последовательно каждое ребро во вспомогательную фронтально проецирующую плоскость: ребро АS - в плоскость D (D2 º А 2 S 2), ребро ВS - в плоскость l (l2 º В 2 S 2), ребро СS - в плоскость å (å2 º С 2 S 2). Определяем линию пересечения каждой вспомогательной плоскости с секущей плоскостью – линии (1121), (3141), (5161). На пересечении линий пересечения и проекций соответствующих ребер определяем искомые точки фигуры сечения (D 1 E 1 F 1), (D 2 E 2 F 2). Задача: Дана прямоугольная пирамида и прямая общего положения l (рис. 6.4). Определить точки пересечения прямой и пирамиды. Решение: Так как прямая l является прямой общего положения, задача решается аналогично задаче нахождение точки пересечения прямой и плоскости. Заключаем прямую l во вспомогательную фронтально проецирующую плоскость å (å2 º l 2). Строим сечение пирамиды вспомогательной плоскостью å (аналогично задаче рис. 6.1). На пересечении горизонтальной проекции прямой l 1 и контуром сечения (112131) находим искомые точки D и E. Определяем видимость прямой относительно точек пересечения с пирамидой.
Развертка многогранника Разверткой поверхности называется плоская фигура, полученная совмещением поверхности с плоскостью. Построение разверток важно для тех видов производства, где продукция изготавливается из листового материала. При проектировании листовых конструкций выполняется построение разверток их поверхностей. При построении развертки многогранника необходимо определить натуральную величину всех его граней.
Существует несколько способов построения разверток: способ нормального сечения, способ раскатки. Рассмотрим построение развертки призмы способом нормального сечения. Задача: Дана треугольная призма (рис. 6.5). Построить развертку поверхности данной призмы.
Решение: Пересечем призму плоскостью Т перпендикулярно ее боковым ребрам. Полученное сечение (123) называется нормальным. Так как ребра призмы в данной задаче являются горизонталями, то след плоскости нормального сечения Т1 перпендикулярен горизонтальным проекциям ребер A 1 F 1, B 1 D 1, C 1 E 1. Определяем натуральную величину нормального сечения призмы плоскостью Т способом вращения вокруг оси i. Фигура (1 Для построения развертки на горизонтальной линии отложим отрезки, равные сторонам нормального сечения 1020 º 1
Кривые поверхности Основные понятия В начертательной геометрии кривая поверхность определяются, как непрерывное множество положений перемещающейся в пространстве линии, называемой образующей. Образующая может быть прямой линией (линейчатая поверхность) или кривой (нелинейчатая). Движение образующей в пространстве может осуществляться по некоторому закону. Такая поверхность называется закономерной, в отличии от незакономерной (случайной) поверхности. К числу условий перемещения в пространстве образующей линии относятся: перемещение по неподвижным линиям - направляющим, вращательное движение вокруг неподвижной оси, винтовое перемещение и др. Одна и та же поверхность может быть образована перемещением различных линий и согласно различных условиям. Например, боковая поверхность прямого кругового цилиндра может быть рассмотрена как результат: - перемещение окружности вдоль некоторой оси; - вращение некоторой образующей прямой линии вокруг оси вращения; - вращение некоторой кривой линии, все точки которой равноудалены от оси вращения. Рассматривая совокупность прямолинейных образующих с совокупностью образующих окружностей получим каркас данной поверхности цилиндра. Множество неподвижных линий, инцидентных данной поверхности и объединенных каким либо общим признаком, называется её каркасом.
Задание поверхности вращения на чертеже. Точки и линии на поверхности На чертеже поверхность изображают очерком проекций поверхности или её отдельных частей. Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этой поверхности. Точка принадлежит поверхности, если она находится на линии, принадлежащей данной поверхности. Рассмотрим чертёж конуса и точки, принадлежащие его поверхности (рис. 6.6). Фронтальная проекция конуса задана очерковыми образующими, определяющими границы поверхности, а горизонтальная – проекцией основания конуса. Каркас конуса – это совокупность образующих прямых линий, соединяющих их вершину S и основание конуса и совокупность параллелей – окружностей различного радиуса, плоскость которых перпендикулярна оси конуса.
Рассмотрим ряд точек на боковой поверхности конуса. Точка А расположена на очерковой образующей конуса, её горизонтальная проекция находится на линии связи, на оси конуса. Обратим внимание, что очерковая образующая является фронталью, т.е. её фронтальная проекция натуральная величина образующей конуса. Принадлежность точек В и С поверхности конуса определяется соответственно с помощью параллели радиуса R или образующей конуса (S 1).
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 862; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |



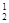 2
2 



