Взаимное расположение двух плоскостей, прямой линии и плоскости

Две плоскости в пространстве могут быть параллельны, в частном случае совпадать, пересекаться, в частном случае бать перпендикулярными.

Аналогично могут быть расположены прямая линия относительно плоскости.

 

 

Параллельные плоскости.

 

Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости (рис. 4.10).

При задании плоскости следами две плоскости параллельны, если параллельны их одноимённые следы (рис. 4.10).

Рис. 4.10. Параллельные плоскости.

Задача: Через току К провести плоскость параллельную заданной плоскости Т (рис. 4.11).

Рис. 4.11.

Решение: Через точку проводим горизонталь h параллельную заданной плоскости Т, т.е. h₁ параллельно Т₁. Найдём фронтальный след горизонтали N (N₁, N₂). Через фронтальный след горизонтали N₂ проведём фронтальный след искомой плоскости Г₂ параллельно фронтальному следу плоскости Т₂, определяется точка схода следов Г_x. Проводим горизонтальный след плоскости Г₁ из Г_x параллельно горизонтальному следу Т₂.

Прямая линия, параллельная плоскости.

Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в плоскости (рис. 4.12).

Через каждую точку пространства можно провести бесконечное множество прямых, параллельных данной плоскости Р.

Рис. 4.12. Прямая линия параллельная плоскости.

Задача: Через точку С провести прямую а параллельную плоскости Р (рис. 4.13).

Рис. 4.13.

Решение: Одну из проекций искомой прямой а ₂ проведём произвольно через точку С ₂. Определим в данной плоскости P прямую параллельную прямой а. Горизонтальная проекция прямой а ₁ будет параллельна горизонтальной проекции прямой в плоскости а ₂ || (1₂2₂) и а ₁ || (1₁2₁).

 

 

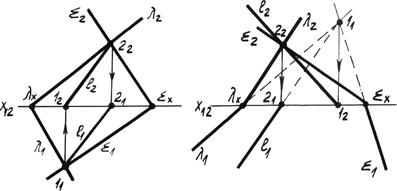
Пересекающиеся плоскости.

Две плоскости пересекаются по прямой линии, для построения которой достаточно, или определить две общие для плоскостей точки, или одну точку и направление линии пересечения.

Рассмотрим задачи на построение проекций линии пересечения плоскостей и их положения относительно плоскостей проекций.

1. Если плоскости заданы следами и следы пересекаются в пределах чертежа (рис. 4.14а) то, две точки линии пересечения определяются на пересечение одноимённых следов. Точка 1 – пересечение горизонтальных следов, точка 2 – пересечение фронтальных следов. Линия l (1₁1₂) - линия пересечения плоскостей l и å.

Рис. 4.14а. Плоскости заданы следами.

2. Один из частных случаев пересечения плоскостей, когда одна из них является проецирующей плоскостью (рис. 4.14б).

Задача сводиться к определению второй проекции линии, принадлежащей и проецирующей плоскости, и плоскости общего положения.

Определяем точки пересечения соответствующего следа проецирующей плоскости с плоскостью общего положения точки 1 и 2. По линиям связи определяем вторую проекцию. Затем необходимо определить видимость отсеков плоскости общего положения относительно линии пересечения.

Рис. 4.14б. Одна из плоскостей проецирующая.

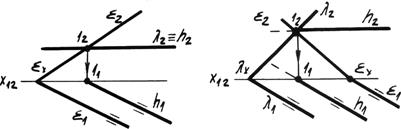
3. В некоторых случаях линия пересечения плоскостей является линией частного положения (рис. 4.14в).

Рассмотрим задачи на пересечение плоскостей по горизонтали. В первой задаче одна из плоскостей l является горизонтальной плоскостью уровня, поэтому фронтальная линия проекции пересечения h ₂ совпадает со следом этой плоскости и является горизонталью. Горизонтальная проекция определяется по точке 1 пересечения следов и направлению h ₁ || l₁.

Рис. 4.14в. Пересечение по линиям частного положения.

Во второй задаче горизонтальные следы плоскостей общего положения параллельны l₁ || å₁. Следовательно, горизонтальная проекция линии пересечения будет им параллельна h ₁ || l₁ || å₁, а фронтальная будет проходить через точку 1 пересечения фронтальных следов.

Аналогичны случаи пересечения по фронтали. Существуют другие частные случаи пересечения плоскостей, когда линией пересечения являются проецирующие прямые.

4. Общий случай пересечение плоскостей, когда в пределах чертежа сразу не определяются общие для данных плоскостей точки. Для решения такой задачи используются вспомогательные секущие плоскости обычно частного положения – или плоскости уровня, или проецирующие.

Рассмотрим пример на рис. 4.15.

Даны две плоскости, заданные параллельными прямыми (а || b) и треугольником АВС. Для определения двух общих точек данных плоскостей решаем задачу по алгоритму:

1. Вводим первую вспомогательную горизонтальную плоскость уровня å.

2. Строим линии пересечения каждой данной плоскости со вспомогательной (а || b) Ç å ® h ^å (ABC) Ç å ® h ^å. Эти линии являются горизонталями данных плоскостей.

3. Определяем точку пересечения линии пересечения. Точка I – общая для данных плоскостей.

Рис. 4.15. Общий случай пересечения плоскостей.

4. Для определения ещё одной общей точки выводим вторую вспомогательную секущую плоскость уровня. l Выполним те же построения и определим вторую общую точку II.

5. Соединяем получившиеся точки I и II, Которые определяют линии пересечения плоскостей l (l ₁, l ₂).

При решении некоторых задач удобнее использовать вспомогательные проецирующие плоскости.