Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямая линия и точка в плоскости общего положенияСодержание книги
Поиск на нашем сайте Из аксиомы принадлежности известно, что прямая принадлежит плоскости, если две точки этой прямой принадлежат той же плоскости. На рис. 4.5а плоскость задана двумя пересекающимися прямыми (m Ç n).
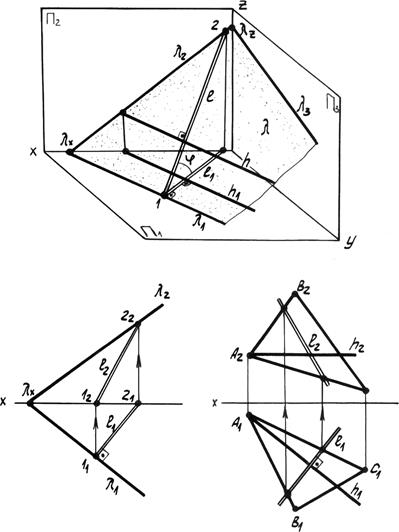
На заданных прямых отметим две произвольные точки А и В, которые определят прямую с, принадлежащую плоскости (m Ç n). Если одна из точек, например А, удалена в бесконечность, т.е. является несобственной, то аксиома принадлежности формулируется так: Прямая линия принадлежит плоскости, если имеет с ней общую точку и параллельна какой-либо прямой, лежащей в плоскости. В данной плоскости (m Ç n) прямая d параллельна прямой m и проходит через точку В. При задании плоскости следами (рис. 4.5б, в) две точки, определяющие принадлежность прямой линии плоскости, будут следами этой прямой линии. На рис. 4.5б фронтальный след N прямой l расположен на фронтальном следе плоскости l2, а горизонтальный след М – на горизонтальном следе плоскости l1.
На тех же примерах рассмотрим точку в плоскости. Точка принадлежит плоскости если она расположена на прямой, принадлежащей плоскости. Отметим на прямой l (рис. 4.5б) точку 1, а на прямой h (рис. 4.5в) точку С. Точка 1 будет принадлежать плоскости l, а точка С – плоскости S, т.к. расположены на прямых, принадлежащим соответствующим плоскостям.
Главные линии плоскости Кроме прямых общего положения в плоскости можно выделить линии частного положения, которые называют главными линиями плоскости – это линии уровня и линии наклона плоскости. 1. Горизонтали плоскости h – прямые, принадлежащие плоскости и параллельные плоскости p1 (рис. 4.6).
На эпюре фронтальная проекция горизонтали h 2 параллельна оси x, а горизонтальная проекция горизонтали h 1 параллельна горизонтальному следу плоскости h 1 || Т1, т.е. горизонтальный след плоскости – это тоже её горизонталь. 2. Фронтали плоскости ¦ – прямые, принадлежащие плоскости и параллельные плоскости p2 (рис. 4.7). На эпюре горизонтальная проекция фронтали ¦1 параллельна оси x 1, а фронтальная проекция фронтали параллельна фронтальному следу плоскости ¦2 || Г2, т.е. фронтальный след плоскости – это тоже фронталь плоскости.
3. Профильные прямые плоскости p – прямые, принадлежащие плоскости и параллельные плоскости p3 (рис. 4.8).
На эпюре горизонтальная и фронтальная проекции профильной прямой р 1 и р 2 перпендикулярны оси x, а профильная проекция профильной прямой р 3 параллельна профильному следу р 3 || q3, т.е. профильный след плоскости – это тоже её профильная прямая. 4. Линия наибольшего наклона плоскости l – это прямая, принадлежащая плоскости и перпендикулярная к соответствующей линии уровня плоскости. С помощью линии наибольшего наклона определяется угол наибольшего наклона плоскости к соответствующей плоскости проекции. Линия l, перпендикулярная горизонтальной плоскости, определяет угол наклона плоскости к плоскости p1 (рис. 4.9). Если плоскость задана следами, то горизонтальная проекция линии наибольшего наклона плоскости перпендикулярна горизонтальному следу l1 (рис. 4.9). Если плоскость задана другим способом, необходимо построить горизонталь плоскости, тогда горизонтальная проекция линии наибольшего наклона определяется перпендикулярно горизонтальной проекции горизонтали, l 1 ^ h 1. Аналогично можно построить линии наибольшего наклона к другим плоскостям проекции.
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 495; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.006 с.) |