Пересечение плоскостей. Два способа нахождения линии пересечения плоскостей.

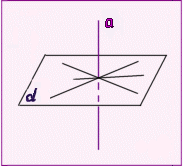
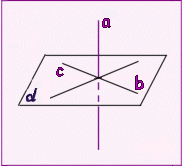
В случае задания плоскостей их следами: если хотя бы одна пара одноименных следов пересекается, то плоскости пересекаются.

Если плоскости заданы другим способом:

Общий способ нахождения линии пересечения (основан на использовании вспомогательных плоскостей-посредниц)

1. Задаем вспомогательную плоскость и находим линии ее пересечения с заданными плоскостями – 12 и 34

2. Находим точку пересечения прямых 12 и 34 – первую искомую точку М

3. Задаем вторую вспомогательную плоскость и находим линии ее пересечения с заданными плоскостями – прямые 56 и 78

4. Находим точку пересечения прямых 56 и 78 – вторую искомую точку N

5. Через точки М и N проводим линию пересечения плоскостей

Нахождение линии пересечения на основе пересечения прямой и плоскости.

На одной из плоскостей, заданных например плоской фигурой, выделить сторону и рассматривать ее как прямую, пересекающую вторую плоскость. Аналогично берется вторая прямая и строится вторая точка пересечения плоскостей.

Алгоритм захождения точки пересечения прямой и плоскости:

1. Заключаем прямую во вспомогательную плоскость

2. Находим линию пересечения заданной и вспомогательной плоскости – прямую 12

3. Точка пересечения М и 12 – точка К – искомая точка пересечения (точка пересечения прямой и плоскости)

4. Определяем видимость прямой

 

Перпендикулярность прямой и плоскости. Теорема о проекциях прямого угла.

Определение
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.

ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

Для того, чтобы прямая m была перпендикулярна плоскости s, необходимо и достаточно, чтобы горизонтальная проекция прямой m₁ была перпендикулярна горизонтальной проекции горизонтали (m₁ перпендикулярна h₁), а фронтальная проекция прямой m₂ – фронтальной проекции фронтали (m₂ перпендикулярна f₂).

 

Теорема о проецировании прямого угла:

Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину.

Следствие: если прямоугольная проекция угла, одна сторона которого параллельна плоскости проекций, - прямой угол, то проецируемый угол также прямой.

 

Перпендикулярность плоскостей. Перпендикулярность прямых.

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90 градусам.

 

- Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

- Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.

- Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.

 

Построение плоскости β, перпендикулярной к плоскости α, может быть произведено двумя способами

1. пл.β проводится через прямую, перпендикулярную плоскости к пл.α

2. пл.β проводится перпендикулярно к прямой, лежащей в пл.α или параллельной этой плоскости

 

Перпендикулярность прямых

Две взаимно-перпендикулярные прямые (пересекающиеся или скрещивающиеся) тогда и только тогда проецируются на горизонтальную плоскость в виде перпендикулярных прямых, когда хотя бы одна из этих прямых является горизонталью.

Аналогично для фронтальной и профильной плоскостей.

 

 

13. Преобразование ортогональных проекций: методы вращения и замены плоскостей. Использование методов преобразования для решения типовых задач.

1. Метод замены плоскостей проекций: сущность метода заключается в том, что положение точек, линий, плоских фигур, поверхностей в пространстве остается неизменным, а система П1, П2 дополняется плоскостями, образующими с П1 или П2, или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.

2. Метод вращения

Некоторая фигура вращается вокруг некоторой неподвижной прямой(ось вращения). И при вращении каждая точка вращаемой фигуры перемещается в плоскости перпендикулярной к оси вращения(плоскость вращения). Точка перемещается по окружности, центр которой находится в точке пересечения оси с плоскостью вращения (центр вращения), а радиус окружности равняется расстоянию от вращаемой точки до центра (это радиус вращения). Если какая-либо точка данной системы находится на оси вращения, то при вращении системы эта точка считается неподвижной. Ось вращения может быть задана или выбрана.