
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Передача электрической энергии по линии постоянного токаСодержание книги
Поиск на нашем сайте
Цель работы: изучение основных свойств линии электропередачи постоянного тока посредством исследования эквивалентной электрической цепи (модели). Программа работы
1. Собрать схему экспериментальной установки, эквивалентной передаче энергии от генератора к потребителю (рис. 2.1). В этой схеме
Рис. 2.1 ГН – генератор стабилизированного напряжения; Rл, Rн – сопротивления линии передачи и нагрузки; рV1 , рV2, рА - измерительные приборы
2. Изменяя сопротивление нагрузки от Rн = 0 (режим короткого замыкания) до Rн = ∞ (режим холостого хода), получить 10 значений тока и напряжений на генераторе U1 и потребителе U2. 3. Вычислить: мощность генератора P1; мощность, потребляемую нагрузкой Р 2, потери мощности Δ P и напряжения Δ U в линии электропередачи, сопротивления линии передачи Rл и нагрузки Rн, кпд (η) линии электропередачи. Значения измеряемых и расчетных величин занести в таблицу 2.1. Таблица 2.1
4. Построить зависимости: U 1 = f (I), U 2 = f (I), Δ U = f (I), P 1 = f (I), P 2 = f (I), Δ P = f (I), η = f (I) и определить по ним величину максимально возможной передаваемой мощности Р2 и соответствующие ей значения U2 и η. Теоретические положения
При передаче энергии от генератора к потребителю по линии электропередачи их сопротивления включены последовательно (делитель напряжения). Не учитывая внутреннее сопротивление генератора, его напряжение определится как: U 1 = U 2 + Δ U, откуда потери напряжения в линии передачи будет: Δ U = U 1 – U 2 = I · Rл. (2.1) Ток, проходящий по линии передачи, нагревает провода (закон Джоуля-Ленца), в результате чего часть мощности генератора теряется (потери мощности в линии передаче – Δ P): Δ P = P 1 – P 2 = I 2 · Rл, (2.2) где P 1 = U 1 · I – мощность, вырабатываемая генератором; P 2 = U 2 · I – мощность потребителя.
Потери напряжения и мощности в линии электропередачи нежелательны, но неизбежны. Они определяют экономичность передачи энергии, кпд линии электропередачи:
При изменении нагрузки от режима холостого хода (I = 0) до короткого замыкания ( P 1 = U 1 · I, U 2 = U 1 – Δ U = U 1 – Rл · I, Δ U = Rл · I,
Потери мощности в линии передачи находятся в квадратичной зависимости от тока (2.2). Что касается мощности, затрачиваемой в потребителе энергии, то она определяется уравнением второго порядка:
Изменяясь от нуля при I = 0 (холостой ход) до нуля при Rн = 0 (режим короткого замыкания) имеет один экстремум. Условие передачи потребителю максимальной мощности получим, приравняв к нулю, первую производную мощности по сопротивлению нагрузки:
Откуда следует, что максимум передаваемой мощности будет при Rн = Rл . При этом КПД линии передачи будет равен 0,5, а напряжение на потребителе будет составлять половину напряжения генератора. Характер изменения параметров линии передачи приведен на рисунке 2.2.
Рис. 2.2
Различают следующие режимы работы линии электропередачи: 1. Номинальный – длительный режим работы, на который проектируется линия передачи, обеспечивая номинальное напряжение на потребителе при допустимых нормированных отклонениях от номинала, высокий КПД передачи. 2. Согласованный – обеспечивает максимум мощности, передаваемой от генератора к потребителю. 3. Холостой ход – потребитель отключен, ток в линии передачи и передаваемая мощность равны нулю. 4. Короткое замыкание – это аварийный режим, ток в линии передачи максимальный, а передаваемая мощность равна нулю. Основным рабочим режимом является номинальный. Анализ зависимостей (1, 2, 3) показывает, что снижение потерь напряжения, мощности в линии передачи, получение высокого кпд (более 90%) можно достигать двумя путями: уменьшением сопротивления линии передачи и повышением напряжения генератора. Первый путь требует увеличения сечения проводов и соответственно затрат, второй ограничен допустимым напряжением на потребителе. В конечном итоге выбор решения определяется технико-экономическими и экологическими соображениями.
Согласованный режим применяется в том случае, когда потери мощности в линии передачи пренебрежительно малы (доли ватта), а передача максимальной мощности необходима для работы устройств, например, при передаче сигнала от датчиков генераторного типа в системах автоматики.
Контрольные вопросы
1. Как уменьшить потери напряжения и мощности в линии электропередачи при за данной мощности потребителя? 2. Условие передачи максимальной мощности по линии электропередачи? 3. Как повысить кпд линии электропередачи?
Лабораторная работа № 3
Исследование разветвленной электрической цепи постоянного тока с двумя источниками ЭДС
Цель работы: приобретение практических навыков анализа сложной цепи постоянного тока. Экспериментальная проверка справедливости законов Кирхгофа и закона сохранения энергии (баланс мощностей). Приобретение навыков построения и пользования потенциальными диаграммами.
Программа работы 1. Собрать схему экспериментальной установки (рис. 3.1).
Рис. 3.1
2. Произвести измерения ЭДС генераторов напряжения ГН1 и ГН2 (Е1, Е2), напряжений на участках цепи, токов в ветвях. При этом одновременно определить направление токов в ветвях и показать на схеме. Условным положительным направлением тока является направление движения положительного заряда (от «+» к «-»). Если стрелка прибора отклоняется вправо, то «+» прибора совпадает с «+» в схеме и соответственно определяется направление тока в ветви. Данные измерений занести в таблицу 3.1.
3. Записать параметры резисторов R1 - R5, рассчитать токи I4, I5, построить потенциальную диаграмму для контура, заданного преподавателем, и проверить справедливость законов Кирхгофа. Составить баланс мощностей для контура ГН1, R1, R3, ГН2, R2, ГН1, учитывая режим работы источников ЭДС. Теоретические положения В разветвленных электрических цепях используют следующие понятия: 1) ветвь – участок цепи с последовательным соединением элементов; 2) узел – точка соединения нескольких ветвей; 3) контур – любой замкнутый путь по цепи с началом и концом в одной точке. При расчете таких цепей применяют законы Кирхгофа: Первый закон Кирхгофа. Алгебраическая сумма токов (рис. 3.2), сходящихся в узле, равна нулю. Токи, подходящие к узлу, берут с одним знаком, выходящие – с другим, или сумма токов, подходящих к узлу, равна сумме токов, выходящих из узла: I1 – I2 – I3 – I4 + I5 = 0 или I1 + I5 = I2 + I3 + I4
Рис. 3.2
Второй закон Кирхгофа. В любом замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений: Σ Е = Σ U = Σ I · R. Правило выбора знака: произвольно задаемся направлением обхода контура и, если ЭДС, напряжение, ток совпадают с направлением обхода, берутся со знаком «плюс», не совпадают – «минус». Например, для контура на рисунке 3.3 имеем: Е1 – Е2 = I1R1 – I3R3 – U2 + I4R4.
Рис. 3.3
В сложных цепях источники ЭДС могут работать в режиме генератора и потребителя энергии. Если направление ЭДС совпадает с направлением тока в этой ветви, то источник ЭДС работает генератором, т.е. отдает энергию в цепь; если не совпадает, то этот источник ЭДС является потребителем энергии.
Баланс мощностей
В любой электрической цепи выполняется закон сохранения энергии: сколько энергии вырабатывают генераторы, столько ее и потребляется. В единицу времени это будет закон сохранения мощностей или баланс мощностей: мощность генераторов в данной цепи равна мощности всех потребителей: Σ Рг = Σ Рн. В сложных цепях источники ЭДС могут работать в режиме генератора, если направление тока совпадает с направлением ЭДС, и потребителя, если их направления не совпадают. Для источников ЭДС: Р = ЕI; для резистивных элементов: Р = I2R. Проверка баланса мощностей всегда необходима в электрических расчетах, так как первый закон Кирхгофа может соблюдаться и при неправильных расчетах.
Потенциальная диаграмма Под потенциальной диаграммой понимают график распределения потенциалов вдоль какого-либо участка цепи или замкнутого контура. При этом любую точку условно заземляют, т.е. ее потенциал принимают равным нулю. При этом распределение токов в ветвях не изменяется, так как не образуется новых ветвей. Потенциальная диаграмма строится как зависимость потенциала φ точки от сопротивления. По оси абсцисс откладывают сопротивление участков цепи, а по оси ординат – потенциалы. Например, в схеме рисунка 3.4 известны сопротивления, токи, ЭДС.
Рис. 3.4
Дано: Е1 = 80 В, Е2 = 64 В, R1 = 6 Ом, R2 = 4 Ом, R3 = 3 Ом, R4 = 1 Ом, I1 = 6 А, I2 = 5 А, I3 = 11 А. Построим потенциальную диаграмму для контура а, в, Е2, с, d, Е1, a. Точка «а» заземлена. Суммарное сопротивление контура равно 4 + 6 = 10 Ом. Выбираем масштаб для сопротивлений. Внутренним сопротивлением источников ЭДС пренебрегаем. Определим потенциалы точек: φа = 0; φв = φа + I2R2 (потенциал точки в больше, так как ток идет от большего потенциала к меньшему, поэтому I2R2 берется со знаком «плюс»); φс = φв – Е2 (внутри источника ЭДС ток идет от меньшего к большему, т.е. от «минуса» к «плюсу»); φd = φс – I1R1 ; φе = φd + Е1 = φа.
Контрольные вопросы
1. Как с помощью вольтметра или амперметра определить направление тока в ветви? 2. Сформулируйте I и II законы Кирхгофа и правила выбора знаков. 3. Как определить режим работы источника ЭДС при составлении баланса мощностей?
Лабораторная работа № 4
Исследование переходных процессов в цепи постоянного тока с RC -элементами
Цель работы: экспериментально определить закономерности процессов зарядки и разрядки конденсатора в цепи постоянного тока и влияние параметров цепи на переходной процесс.
Программа работы 1. Собрать схему экспериментальной установки (рис. 4.1)
Рис. 4.1
2. Исследовать процесс зарядки конденсатора (выключатель в положении «01») при двух различных параметрах R, C, измеряя величину тока через определенные промежутки времени. Предварительно провести пробную зарядку конденсатора и определить ее время, затем конденсатор полностью разрядить. 3. Зарядить полностью конденсатор и затем, переведя выключатель в положение «02», фиксировать величину тока разрядки через определенные промежутки времени. 4. Результаты измерения по пунктам 2 и 3 занести в таблицу, и по этим данным рассчитать напряжение на конденсаторе и построить график i = f(t), uc = f(t) при зарядке и разрядке конденсатора, по которым определить постоянные времени τз и τр для двух-трех точек кривых зарядки и разрядки.
Таблица 4.1
5. По заданным параметрам R, C построить расчетные характеристики зарядки и разрядки конденсатора и сравнить с экспериментальными.
Теоретические положения
Процессы, происходящие в электрических цепях при переводе их из одного установившегося режима в другой, называются переходными процессами. Причинами переходных процессов могут быть коммутационные изменения режимов (замыкание или размыкание электрической цепи или изменение ее электрических параметров: входного напряжения, величин сопротивлений, емкости, индуктивности). В нашей цепи II закон Кирхгофа для мгновенных значений определяется зависимостью: uR + uC = U0
или iR + uC = U0,
с учетом того, что
где dq = C · duc имеем уравнение:
Произведение RC имеет размерность времени и называется постоянной времени переходного процесса: τ = RC. Это основная характеристика переходного процесса. Физический смысл ее – это время, за которое переходной процесс закончился бы, если бы он шел с постоянной скоростью, т.е. не было бы в цепи элементов, обладающих инерционными свойствами. В нашем случае таким элементом является конденсатор. Он не может зарядиться мгновенно, напряжение на нем не может измениться скачком при подаче напряжения U0. В противном случае составляющая Решая уравнение (4.1) относительно uC, получим: uC = U0 (1 – e –t/τ). (4.2) Это уравнение экспоненты. При t = 0 имеем uC = 0, а при t → ∞, uC → U0 (установившееся значение). Практически переходной процесс можно считать закончившимся при t = 4-5τ. Изменение тока при зарядке конденсатора также идет по экспоненциальному закону:
При t = 0 ток скачком принимает значение Контролируя изменение тока во времени и зная величину R, а, следовательно, напряжение на резисторе: uR = iR, напряжение на конденсаторе в переходном процессе можно определить по формуле: uC = U0 – uR и построить экспериментальную кривую переходного процесса зарядки конденсатора, которая должна совпасть с теоретической кривой, построенной по уравнению (4.2). Проведя касательную в любой точке кривой uC = f(t) до пересечения с установившимся значением напряжения U0, можно определить постоянную времени τ, как проекцию на оси времени от точки касания до точки пересечения с U0. Постоянную времени можно также определить из уравнения (4.3), зная I0 и измерив через небольшой промежуток времени t значение тока i:
Процесс разрядки конденсатора при замыкании цепи R, C описывается дифференциальным уравнением: iR + uC = 0, где uC = U0e –t/τ
Знак «–» перед током показывает изменение направления тока при разрядке конденсатора по сравнению с зарядкой. Измеряя ток и время, можно вычислить напряжение на конденсаторе при разрядке: uC = - iR. Графики изменения uC и i при зарядке и разрядке конденсатора имеют вид:
Зарядка Разрядка
Рис. 4.2
Контрольные вопросы
1. Что называется переходным процессом? 2. При каких условиях появляются переходные процессы? 3. Физический смысл постоянной времени переходного процесса. 4. Отличаются ли постоянные времени при зарядке и разрядке конденсатора? 5. Как определить постоянную времени по графику переходного процесса? 6. Измениться ли продолжительность переходного процесса, если изменять величину напряжения источника питания? 7. По каким зависимостям идут процессы зарядки и разрядки конденсатора? 8. Каким образом можно изменить время зарядки и разрядки конденсатора?
Лабораторная работа № 5
Исследование нелинейных цепей постоянного тока
Цель работы: экспериментальная проверка графоаналитического метода расчета нелинейных цепей.
Программа работы 1.Собрать схему экспериментальной установки (рис. 5.1) и провести измерения для трех опытов.
Рис. 5.1
1-й опыт – включено только нелинейное сопротивление Rн. 2-й опыт – последовательное соединение нелинейного Rн и линейного Rл сопротивлений. 3-й опыт – параллельное соединение нелинейного Rн и линейного Rл сопротивлений. - Установить переключатель SA1 в положение «1», переключатель SA2 в положение «2». Изменяя напряжение U1 от 0 до 30 В (через 5 В), произвести замеры U1 и I1. Результаты измерений занести в таблицу. - Установить переключатель SA1 в положение «2», переключатель SA2 в положение «1». Проверить, что прибор pV2 включен на измерение напряжения. Изменяя U1 от 0 до 30 В произвести измерения U1, I1, U2 = Uн при последовательном соединении линейного и нелинейного сопротивлений. Напряжение на линейном сопротивлении рассчитать по формуле Uл = U1 – U2. - Установить переключатель SA1 в положение «1», переключатель SA2 в положение «1», измерительный прибор pV2 переключить на измерение тока I2 = Iл и провести измерение U1, I1, I2 = Iл. Имеем параллельное соединение линейного и нелинейного сопротивлений. Ток в нелинейном сопротивлении определить по I закону Кирхгофа: Iн = I1 – I2.
Таблица измерений и расчетов
2. По данным измерений 1-го опыта построить вольтамперную характеристику ВАХ нелинейного сопротивления I1 = f(U1), ВАХ линейного сопротивления построить по расчету, определив угол наклона ВАХ к оси ординат, задавшись напряжением и определив величину тока. Например, U1 = 30 B, ток По результатам 2-го и 3-го опыта нанести экспериментальные точки на характеристики соединений и оценить совпадение графоаналитического построения ВАХ с результатами экспериментов.
Теоретические положения Нелинейной называется электрическая цепь, имеющая хотя бы один элемент, ВАХ которого не является прямой линией. В нелинейных цепях не соблюдается закон Ома. И методы расчета линейных цепей приводят к большим погрешностям, зачастую недопустимых. Наиболее простым методом расчета нелинейных цепей является графоаналитический, когда по ВАХ элементов цепи строят графически ВАХ их соединений. При последовательном соединении, задаваясь значениями тока, результирующую характеристику получают суммированием напряжений элементов цепи: U= =Uл + Uн +... (рис. 5.2).
Рис. 5.2
При параллельном соединении, задаваясь величиной напряжения, ВАХ соединения получают суммированием токов I = Iл +Iн +... (рис. 5.3).
Рис. 5.3
При смешанном соединении сначала находят ВАХ параллельного соединения, затем последовательного. В конечном итоге мы преобразуем схему соединения к одному сопротивлению так же, как делаем это при эквивалентном преобразовании разветвленных линейных цепей. Только делаем это графически. А затем для заданного напряжения в обратной последовательности находим токи и напряжения в элементах схемы.
Контрольные вопросы
1. Какая цепь называется нелинейной? 2. Методика определения напряжений на элементах нелинейной цепи при последовательном соединении. 3. Методика определения токов в нелинейной цепи при параллельном соединении элементов. 4. Расчет нелинейной цепи при смешанном соединении элементов.
Лабораторная работа № 6
Исследование цепи переменного тока с последовательным соединением r, L, C-элементов
Цель работы: исследовать особенности работы цепи при последовательном соединении активных, индуктивных и емкостных сопротивлений, научиться анализировать работу цепи с помощью построения векторных диаграмм.
Программа работы 1. Изучить схему замещения экспериментальной цепи (рис. 6.1)
Рис. 6.1
2. Измерить и рассчитать параметры цепи для трех опытов (табл. 6.1): а) включена реальная катушка индуктивности (выключатели QW1 и QW2 замкнуты); б) включены катушка и активное сопротивление (QW1 разомкнут, QW2 замкнут); в) включены катушка, активное сопротивление и конденсатор (QW1 и QW2 разомкнуты). 3. Вычислить параметры цепи и построить в масштабе векторные диаграммы напряжений и тока для каждого опыта, а также треугольники мощностей. 4. Рассчитать емкость конденсатора для получения резонанса напряжений при последовательном включении катушки и конденсатора, а также напряжения на элементах схемы для этого варианта.
Таблица 6.1
Теоретические положения
На переменном токе различают три вида идеальных сопротивлений, определяющих различный характер электромагнитных процессов в таких цепях: активное r, индуктивное xL и емкостное хС. Последние два называются реактивными сопротивлениями. Это позволяет реальные приемники электроэнергии изображать схемами замещения в виде соединения идеальных сопротивлений и проводить электротехнические расчеты, отражающие суть физических процессов в цепях переменного тока. Идеальное активное сопротивление r. Это приемники, для которых можно пренебречь наличием переменных магнитных полей и связанных с этим явлений самоиндукции и скинэффекта (вытеснение тока из центра проводника к поверхности, в результате чего сопротивление возрастает); а также пренебрегаем возможностью накапливания электрических зарядов. В таком сопротивлении напряжение и ток совпадают по фазе, электрическая энергия безвозвратно превращается в другой вид энергии (тепло, свет и др.). Примерами таких сопротивлений являются лампы накаливания, резисторы, нагреватели. Потребляемая ими средняя мощность за период называется активной и измеряется в ваттах (Вт): P = Ur · I. Идеальное индуктивное сопротивление xL. Если на сердечник из ферромагнитного материала намотать катушку из сверхпроводника (r = 0), включит в цепь переменного тока, то в связи с появлением ЭДС самоиндукции величина тока будет ограничена, а ток отстает по фазе от напряжения UL на 90 электрических градусов. Мгновенная мощность р изменяется с двойной частотой. Средняя мощность за период Р равна нулю. Четверть периода мощность потребляется из сети, превращаясь в энергию магнитного поля, а во вторую четверть возвращается в сеть, преобразуясь в электрическую энергию. Амплитудное значение мощности за четверть периода называется реактивной мощностью (QL = UL · I) измеряется в ВАр (вольт-ампер реактивный). Идеальное емкостное сопротивление xС. При включении в цепь переменного тока конденсатора амперметр покажет постоянное наличие тока в цепи. Это не означает, что ток проходит через изоляцию между обкладками конденсатора. Это будет пробой конденсатора. Физика процессов заключается в том, что четверть периода конденсатор заряжается, потребляя энергию из сети, а вторую четверть разряжается, отдавая энергию обратно в сеть, т.е. энергия циркулирует между генератором и приемником так же, как в идеальном индуктивном сопротивлении с двойной частотой. Средняя мощность за период Р равна нулю, а амплитудная за четверть периода (QC = UC · I) также называется реактивной. Ток в такой цепи опережает напряжение UC на 90 электрических градусов. Напряжения UL и UC, а также реактивные мощности QL и QC находятся в противофазе (сдвинуты друг относительно друга во времени на 180 электрических градусов). Реальные сопротивления. В реальных приемниках электроэнергии на переменном токе наблюдаются одновременно все те физические процессы, которые отмечены для идеальных сопротивлений. Степень возможностей идеализации определяется требуемой точностью инженерных расчетов. С учетом этого реальные приемники можно представить в виде схемы замещения, состоящей из идеальных сопротивлений. При их последовательном соединении ток в цепи одинаков, напряжение на участке цепи находится по закону Ома, напряжение на нескольких элементах определяется векторной суммой напряжений участков. Характеристики участков цепи переменного тока при последовательном соединении элементов приведены в таблице 6.2. В общем случае в результате векторного сложения напряжений по участкам цепи образуется треугольник напряжений; разделив его стороны на ток, получим треугольник сопротивлений, а умножив на ток – треугольник мощностей. По ним находятся формулы для расчета неизвестных параметров. Таблица 6.2
Резонанс напряжений. Если xL = xC, то полное сопротивление цепи будет минимальным z = r, ток – максимальным, а UL = UC, U = U r. Это состояние цепи называется резонансом напряжений. При x(L,C) >> r напряжения на реактивных элементах L, C будут значительно превышать напряжение сети. Это используется в телеуправлении, автоматике для выделения полезного сигнала. Резонанс напряжений возможен при любых параметрах L, C при определенной частоте тока, называемой резонансной ω: xL = xC где Из этих же соотношений при известной частоте тока и величины одного из параметров (L или C) можно рассчитать величину второго параметра для получения резонанса. В электротехнике последовательное соединение r, L, C -элементов встречается, например, в конденсаторных двигателях, причем индуктивное сопротивление обмотки и соответственно напряжение обычно на порядок больше ее активного сопротивления. При резонансе повышение напряжения на обмотке и конденсаторе может быть опасным как для оборудования, так и для персонала.
Порядок расчетов
1-й опыт. Включена только реальная катушка индуктивности (r 1, L). Расчет параметров: 1. Полная мощность: S=U · I. 2. Коэффициент мощности: 3. Полное сопротивление катушки: 4. Активное сопротивление катушки: r 1 = z · cosφ. 5. Индуктивное сопротивление катушки: xL = z · sinφ или
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.158.142 (0.014 с.) |



 ) изменяются все параметры линии электропередачи. При стабилизированном напряжении генератора U 1 = const и неизменном сопротивлении линии передачи параметры P 1, U 2, Δ U, η изменяются в функции тока по линейным зависимостям:
) изменяются все параметры линии электропередачи. При стабилизированном напряжении генератора U 1 = const и неизменном сопротивлении линии передачи параметры P 1, U 2, Δ U, η изменяются в функции тока по линейным зависимостям: . (2.3)
. (2.3)









 . (4.1)
. (4.1) и II закон Кирхгофа не будет соблюдаться.
и II закон Кирхгофа не будет соблюдаться. (4.3)
(4.3) и затем уменьшается до нуля при t → ∞.
и затем уменьшается до нуля при t → ∞. .
.


 . Зная ВАХ линейного и нелинейного сопротивлений, построить ВАХ при их последовательном и параллельном соединении.
. Зная ВАХ линейного и нелинейного сопротивлений, построить ВАХ при их последовательном и параллельном соединении.










 )
)
 φ)
φ)
 φ = 0
φ = 0
 π / 2
φ = π / 2 –
отстающий
π / 2
φ = π / 2 –
отстающий
 φ = π / 2 –
опережающий
φ = π / 2 –
опережающий
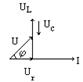 UL>UC
φ >0
UL>UC
φ >0

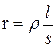















 .
.
 .
. .
. .
. .
. 


