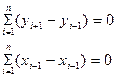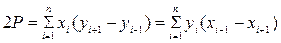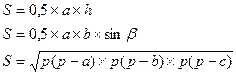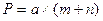Построение профиля местности по заданной линии

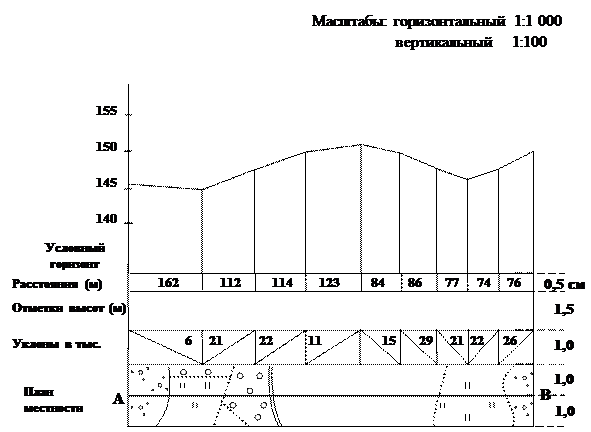
Профиль – уменьшенное изображение вертикального разреза участка земной поверхности. Построение продольного профиля АВ на миллиметровой бумаге выполняется в следующем порядке:

• на плане прочерчивают линию АВ, в обе стороны от нее откладывают расстояние по 1 см и отграничивают участок прямоугольной формы (рис.6.5.);

• в нижней половине миллиметровой бумаги строят разграфку профиля по длине заданной линии АВ, слева от каждой графы подписывают ее название (рис. 6.6.);

Рис. 6.5 План местности на линии построения продольного профиля

(по Неумывакину, 1985).

 

• с помощью измерителя наносят контуры ситуации с карты или плана в графу «План местности» и вычерчивают нанесенные объекты соответствующими условными знаками;

• на плане отмечают точки пересечения профильной линии с горизонталями и характерные точки перегибов местности, нумеруют их по порядку;

• на профиле указывают вертикальный и горизонтальный масштабы его построения. В горизонтальном масштабе откладывают, раствором измерителя, расстояния между отмеченными точками (графа «Расстояния»), в вертикальном – отметки точек на перпендикулярах. Вертикальный масштаб, как правило, в 10 раз крупнее горизонтального.

• раствором измерителя переносят расстояния между отмеченными точками в графу «Расстояния», одновременно по масштабной линейке определяют значения этих расстояний и записывают в соответствующих интервалах данной графы;

• по подписям горизонталей определяют отметки высот точек их пересечения с профильной линией, отметки высот характерных точек определяют интерполированием с округлением до 0,1 м, полученные значения записывают в графу «отметки высот»;

• для верхней линии разграфки, принятой за условную уровенную поверхность, выбирают условное значение высоты с таким расчетом, чтобы чертеж был компактным. На перпендикулярах к верхней линии разграфки откладывают значения высот, уменьшенные на величину высоты условной уровенной поверхности. Концы отрезков соединяют прямыми линиями и получают профиль местности участка АВ.

Вычисляют уклоны между точками профиля и выписывают их значения в тысячных долях единицы (например, 6 или 0,006). Направления уклонов показывают условными линиями, которые проводят в соответствующих интервалах от верхнего угла к нижнему (при отрицательном уклоне), и от нижнего – к верхнему (при положительном уклоне).

 

Рис. 6.6. Продольный профиль по линии АВ,

 

 

Масштаб уклонов – представляет собой номограмму для определения уклонов по карте или плану, строится следующим образом. Определяется горизонтальное проложение для различных значений i (например, 0,02, 0,04, 0,06 и т.д.) по формуле:

Затем откладывают их на соответствующих перпендикулярах к прямой линии, через равные произвольные промежутки. Концы перпендикуляров соединяют плавной кривой.

М 1:10 000 h=10 м Рис. 6.7. Масштаб уклонов

 

 

Масштаб заложений – п редставляет собой номограмму для определения углов наклона по карте или плану, строится следующим образом. Определяется горизонтальное проложение для различных углов наклона (например, 1°, 2°, 3° и т.д.) по формуле:

 

М 1:10 000 h=10 м Рис. 6.8. Масштаб заложений

 

Затем откладывают их на соответствующих перпендикулярах к прямой линии, через равные произвольные промежутки. Концы перпендикуляров соединяют прямыми линиями.

 

Задание

1. По топографической карте определить отметки точек, вычислить уклоны линий, определить их превышения.

2. Построить продольный профиль по топографической карте.

Порядок выполнения работы

Задание 1. По топографической карте, полученной в работе №4, определить высоты всех вершин полигона, вычислить значения уклонов по сторонам полигона.

Задание 2. На миллиметровой бумаге построить продольный профиль по линии, указанной на топографической карте, полученной в работе №4.

Определение площади участка.

Цель работы: научиться вычислять площади земель по карте различными способами.

 

Общие сведения

Аналитический способ – площади определяются по результатам измерений линий и углов на местности или по координатам точек полигона с применением формул геометрии, тригонометрии и аналитической геометрии.

Общая формула для нахождения площади любого n-угольника имеет вид:

Из этой формулы получают большое число других формул, выражающих площадь полигона через приращения координат и координаты вершин, например:

но здесь

Поскольку здесь обе части равенства представляют сумму произведения абсциссы каждой точки на ординату этой же точки. Тогда получим:

Теперь произведем замену:

Потому что, обе части этого равенства представляют суммы произведений абсциссы каждой точки на ординату последующей точки. Тогда выражение приобретет вид:

т.е удвоенная площадь полигона равна сумме произведений каждой ординаты на разность абсцисс предыдущей и последующей точек.

Аналогично получают выражение:

Контроль вычислений ведется по формулам:

Приведем другие формулы нахождения площади полигона через приращения координат и координаты вершин без вывода:

Графический способ – площади определяются по результатам измерений линий по карте или плану, когда участок, изображенный на плане (или карте) предварительно разбивается на простейшие геометрические фигуры, треугольники, прямоугольники и трапеции (Рис. 7.1). Сумма площадей геометрических фигур дает площадь участка. К геометрическому способу относится также вычисление площади при помощи палеток.

Рис. 7.1. Геометрические фигуры и их элементы.

 

Формулы для вычисления площади треугольника (рис.7.1. а):

Формулы вычисления площади трапеции (Рис. 7.1. б):

Формулы вычисления площади четырехугольника (Рис. 7.1.с, в)

Палетка – представляет собой лист стекла, целлулоида, кальки или другого прозрачного материала, разграфленного тонкими линиями на квадраты (квадратная палетка) или параллельные прямые (параллельная палетка).

Квадратная палетка – сеть взаимно перпендикулярных линий, проведенных через 1 или 2 мм. Площадь определяется подсчетом клеток палетки наложенной на фигуру, доли клеток, рассекаемы контуром учитываются на глаз. Зная площадь одного квадрата, которая зависит от масштаба плана, площадь всей фигуры определяется по формуле:

где, s – площадь одного квадрата, в масштабе плана;

n – число целых квадратов, уложившихся в определяемой площади;

m – число квадратов, определенное из их частей, рассеченных контуром.

Для упрощения подсчетов через 0,5 или 1 см проводят утолщенные линии, чтобы число клеток можно было считать группами. Для контроля площадь данного участка измеряют повторно, развернув палетку на 45°.

Параллельная палетка – ряд параллельных линий, проведенных преимущественно через 2 мм (от 2 до 5 мм). Площадь контура этой палетки вычисляют следующим образом. Накладывают ее на план так, чтобы крайние точки контура участка 1 и 16 находились посередине между линиями палетки (рис. 7.2.) В результате участок расчленяется на отдельные трапеции с высотой h и средними линиями s_2-3, s_4-5, …, s_14-15, которые измеряют в масштабе плана (основания трапеция изображены пунктиром). Поскольку площадь каждой трапеции равна произведению s_i ×h, то общая площадь участка составит:

 

Рис. 7.2. Определение площади контура параллельной палеткой.

 

Сумму расстояний Σs_i последовательно набирают в раствор измерителя: взяв расстояние s_2-3, переносят левую иглу измерителя в точку 5, а правую устанавливают на продолжение линии 4-5 в точке k, после чего увеличивают раствор измерителя перемещением левой иголки в точку 4. Тогда в растворе измерителя 4-k будет набрана сумма средних линий (s_2-3+ s_4-5). Дальнейшее измерение продолжают в той же последовательности. Если в процессе набора расстояний раствор измерителя окажется больше размере палетки по ее длине АВ, то сумму средних линий набирают по частям в несколько приемов. Общую длину измеренных средних линий определяют по масштабной линейке и умножают на высоту h, соответствующую числу метров в масштабе плана, затем полученную площадь переводят в гектары.

Для контроля измеряют площадь при втором положении палетки, развернув ее на 60-90° относительно первоначального положения. Относительная погрешность определения площади палеткой составляет 1:50 – 1:100. Квадратную палетку рекомендуется использовать при определении полигона площадью до 2 см² , параллельную – до 10 см².

Механический способ – площади определяются по плану или карте при помощи специальных приборов – планиметров (Рис. 7.3.).

Планиметр – механический или электронный прибор, который путем обвода плоской фигуры любой формы определяет ее площадь. Планиметры делят на линейные – у которых, все точки прибора обвода фигуры подвижны, и полярные – у которых одна точка (полюс) во время обвода неподвижна.

Площадь фигуры вычисляют следующим образом. Перед началом обвода индекс 5 устанавливают в исходной точке контура и берут отсчет n₁ по счетному механизму. Удерживая индекс на линии контура, обводят фигуру по ходу часовой стрелки до исходной точки и берут отсчет n₂. после обвода Полученная разность отсчетов Δn= n₂.– n₁ показывает длину пути счетного ролика, выраженную в делениях планиметра, или иначе количество делений τ, соответствующее площади обведенной фигуры.

Рис. 7.3. Полярный планиметр (а) и схеме его счетного механизма (б)

(по Маслову, 2006).

1 – шарнирное соединение рычагов; 2 – обводной рычаг; 3 – полюсный рычаг; 4 – полюс; 5 – обводной индекс; 6 – опорный винт (штифт); 7 – счетный ролик; 8 – верньер (нониус); 9 – циферблат счетного механизма.

 

Отсчет по счетному механизму состоит из четырех цифр (рис. 22, б). Первая цифра показывает количество оборотов, сделанных циферблату 9, если указатель стоит между двумя цифрами, то читается меньшая цифра. Вторая цифра показывает десятые доли оборота счетного ролика 7 и читается на счетном ролике относительно нуля верньера 8, десятые доли оборота ролика подписаны. Третья цифра показывает сотые доли оборота, которые читаются между штрихом, обозначающим десятые доли оборота и нулем верньера. Четвертая цифра показывает тысячные доли оборота, которые читаются на верньере по штриху, совпадающему с каким-либо штрихом счетного ролика.

Для контроля изменений обводы выполняют не менее двух раз, допустимые расхождения составляют не более 3 делений для площади фигуры до 200 см² и 4 делений для – 400 см². Если расхождения допустимы, то из двух результатов получают среднее.

Площадь фигуры, определяемую обводами планиметра с установкой полюса вне фигуры, вычисляют по формуле:

где, р – цена деления планиметра, т.е. площадь соответствующая одному делению τ.

где, R – длина обводного рычага;

М – знаменатель численного масштаба плана.

Для практического определения цены деления р многократно обводят фигуру с известной площадью при фиксированной установке обводного рычага R. В качестве такой фигуры обычно берут 2-3 квадрата координатной сетки. Чтобы повысить точность измерений, фигуру обводят не менее четырех раз: дважды при положении механизма справа (МП) и дважды при положении механизма слева (МЛ). Результаты измерений заносятся в специальный бланк (прил. 4)

При обводе фигуры должны соблюдаться следующие требования:

1.План укладывают, выпрямляют и закрепляют на ровной поверхности.

2. Полюс планиметра устанавливают с таким расчетом, чтобы при обводе фигуры угол между рычагами θ был не менее 30° и не более 150°, а его отклонения в обе стороны от величины 90° были бы примерно одинаковы.

3. Исходную точку установки обводного индекса выбирают на контуре с таким расчетом, чтобы при движении планиметра в начале и в завершении обвода счетный ролик совсем не вращался или его вращение было бы медленным.

Задание

1. Вычислить площадь полигона по пунктам с известными прямоугольными координатами.

2. Вычислить площадь полигона по топографической карте, полученной в работе №4, графическим и механическим способом.

Порядок выполнения работы

Задание 1. Вычислить площадь полигона по пунктам с известными прямоугольными координатами, по результатам вычислений заполнить ведомость (табл. 9). Вычисления проводить по исходным пунктам в соответствии с вариантом задания (табл. 10).

Таблица 7.1

Ведомость вычисления площади полигона по его вершинам

№ вершины	Координаты, м
xi	yi	yi+1– yi-1	xi-1–x+1	xi (yi+1– yi-1)	yi (xi-1–xi+1)

 

 

Таблица 7.2.

Контрольные задания для вычисления площади полигона аналитическим способом.

№ вари-анта	координаты исходных пунктов
Х	У	Х	У	Х	У	Х	У
	6 134 629,3	9 416 014,3	6 131 421,3	9 484 701,6	6 131 975,2	9 415 881,6	6 132 215,2	9 413 215,1
	6 233 952,4	9 573 914,8	6 133 517,2	9 485 025,7	6 133 952,4	9 413 914,8	6 134 629,3	9 416 014,3
	6 163 952,5	9 163 914,8	6 133 517,2	9 485 025,7	6 233 517,2	9 575 025,7	6 233 952,4	9 573 914,8
	6 131 421,3	9 514 701,6	6 161 421,3	9 514 701,6	6 133 517,2	9 485 025,7	6 131 258,4	9 484 701,6
	6 131 975,2	9 415 881,6	6 133 415,9	9 517 608,2	6 161 421,3	9 514 701,6	6 163 952,5	9 163 914,8
	6 133 952,4	9 413 914,8	6 131 975,2	9 415 881,6	6 133 415,9	9 517 608,2	6 131 421,3	9 514 701,6
	6 134 629,3	9 416 014,3	6 133 952,4	9 413 914,8	6 131 975,2	9 415 881,6	6 132 215,2	9 413 215,1
	6 233 952,4	9 573 914,8	6 233 517,2	9 575 025,7	6 133 952,4	9 413 914,8	6 134 629,3	9 416 014,3
	6 163 952,5	9 163 914,8	6 133 517,2	9 485 025,7	6 233 517,2	9 575 025,7	6 233 952,4	9 573 914,8
	6 131 421,3	9 514 701,6	6 161 421,3	9 514 701,6	6 133 517,2	9 485 025,7	6 131 421,3	9 484 701,6
	6 131 975,2	9 415 881,6	6 133 415,9	9 517 608,2	6 161 421,3	9 514 701,6	6 163 952,5	9 163 914,8
	6 133 952,4	9 413 914,8	6 161 421,3	9 547 521,4	6 133 415,9	9 517 608,2	6 131 421,3	9 514 701,6

Задание 2. Вычислить площадь полигона по топографической карте, полученной в работе №4, графическим способом: разбив ее на простейшие геометрические фигуры, при помощи квадратной и линейной палеток.

Вычислить площадь полигона по топографической карте, полученной в работе №4 механическим способом (прил. 3).

 

СПИСОК ЛИТЕРАТУРЫ

1. Баканова В.В. Геодезия: учебник для вузов / В.В. Баканова; под. общ. ред. Л.М. Комарьковой; М.: Недра, 1980, 277 С.

2. Баршай С.Е. Инженерная геодезия / С.Е. Баршай, В.Ф. Нестеренок, Л.С. Хренов; под общ. ред. Л.С. Хренова; Минск: Высшая школа, 1976, 400С.

3. Дьяков Б.Н. Геодезия: учебное пособие для вузов/ Б.Н. Дьяков; отв. ред. И.В. Лесных; СГГА 2-е изд., перераб. и доп. Новосибирск: СГГА, 1997, 173 С.

4. Измайлов П.И. Практикум по геодезии / П.И. Измайлов; под. общ. ред. И.М. Блудовой; М.: Недра, 1970, 376 С.

5. Маслов А.В. Геодезия / А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков; под общ. ред. В.А. Чураковой; Изд. 6-е перераб. и доп. М.: Колос, 2006, 598С.

6. Михеева Д.Ш. Инженерная геодезия / Д.Ш. Михелев, М.И. Киселев, Е.Б. Клюшин; под ред. Д.Ш. Михелева; 6-е изд. стер. М.: изд. центр Академия, 2006, 480 С.

7. Неумывакин Ю.К. Практикум по геодезии/ Ю.К. Неумывакин, А.С. Смирнов; под общ. ред. Н.Т. Куприной; М.: Недра, 1985, 200 С.

8. Поклад Г.Г. Геодезия: учебное пособие ля вузов/ Г.Г. Поклад, С.П. Гриднев; Воронеж. гос. аграрн. унив-т., М.: Академический проект, 2007, 592С.

9. Петерс И. Шестизначные таблицы тригонометрических функций / И. Петерс; под. общ. ред. Л.М. Комарьковой; М.: Недра, 1975, 300 С.

10. Указания по вычислению площадей: Утв. Гл. управлением землепользования, землеустройства и охраны почв МСХ РСФСР 24.04.74. М., 1974, 48 С.

11. Условные знаки для топографических планов масштабов 1:5 000, 1:2 000, 1:1 000, 1:500: Утв. ГУГК при Совете Мигистров СССР 25.11.86. М.: Картгеоиздат – Геоиздат, 2000, 286 С.

12. Федотов Г.А. Инженерная геодезия / Г.А. Федотов; под общ. ред. Л.А. Савиной; М.: Высшая школа, 2002, 463 С.

13. Чижмаков А.Ф. Практикум по геодезии / А.Ф. Чижмаков, А.М. Кривоченко, В.М. Лазарев [и др.]; под общ. ред. Л.М. Комарьковой; М.: Недра, 1977, 240 С.

14. Южанинов В.С. Картография с основами топографии / В.С. Южанинов; под общ. ред. Ю.Э. Ивановой; М.: Высшая школа, 2001, 302 С.

 

Приложение 1

 

Приложение 2

 

 

Приложение 3

ЗАДАНИЕ

1. Определение прямоугольных и географических координат:

• определить прямоугольные координаты всех вершин полигона (сделать схематический чертеж, показывающий положение точек относительно координатных осей).

• определить географические координаты всех вершин полигона.

Таблица 1.

Определение координат вершин полигона по карте.

№ вершины	Прям. координаты	Геогр. координаты
Х	У	широта	долгота

2. Ориентирование направлений:

• измерить по карте географические азимуты и дирекционные углы всех сторон полигона, вычислить магнитный азимут. Показать все измеренные и вычисленные величины на схематическом чертеже.

• используя измеренные внутренние углы полигона, принимая дирекционный угол α _1-2 за исходный, вычислить последовательно дирекционные углы всех сторон полигона по формуле передачи дирекционного угла. Вычисление углов вести по ходу часовой стрелки.

• по значениям дирекционных углов и азимутов вычислить румбы сторон

Таблица 2.

Определение длин сторон полигона и их ориентирных углов по карте

№ стороны	Длина стороны	Дирекционный угол	Географ. азимут	Магнитный азимут	Румбы
изм. по карте	выч. по формуле	Дирекции-онный	Географи-ческий	Магнит-ный
1-2
2-3
3-4
4-1

3. Обратная геодезическая задача. По плановым координатам вершин полигона определить длины и дирекционные углы всех сторон полигона.

Таблица 3.

Определение длин сторон полигона и их дирекционных углов из решения

обратной геодезической задачи

№ вершины	Прямоугольные координаты	Дирекционный угол	Длина стороны
Х	У

4. Изображение рельефа на топографической карте:

• определить высоты всех вершин полигона.

• вычислить значения уклонов по сторонам полигона.

• построить на миллиметровой бумаге продольный профиль по линии, указанной в задании.

5. Вычисление площади полигона:

• по координатам вершин полигона вычислить площадь полигона.

• вычислить площадь полигона графическим способом

Приложение 4

 

Планиметр №4081 R=133,4 p=0,02

№ сек-ции	Положение полюса	Отсчеты n1, n2 и n3	Разности n1– n2 n2 – n3	Среднее из разно-стей	Площадь в деле-ниях плани-метра	Пло-щадь, га	Поправка	Увязан-ная пло-щадь секций, га	Примечание
I	ПЛ			1590,5		31,80	-0,06	31,74
ПП			1589,5
II	ПЛ					33,72	-0,07	33,65
ПП
III	ПЛ					17,82	-0,06	17,79
ПП

 

 

Содержание

Введение...................................................................................................... 3

Расчетно-графическая работа № 1............................................................. 4

1. Масштабы. Условные топографические знаки..................................... 4

1.1 Масштабы......................................................................................... 4

1. 2 Условные топографические знаки.................................................. 9

2. Ориентирование направлений............................................................. 11

3. Номенклатура и разграфка топографических планов и карт............ 18

Расчетно-графическая работа № 2....................................................... 26

4. Определение географических и прямоугольных координат точек и ориентирных углов направлений по карте............................................................................... 26

5. Прямая и обратная геодезическая задача........................................... 29

6. Основные формы рельефа. Задачи решаемые на топографических картах и планах. 33

7. Определение площади участка........................................................... 40

СПИСОК ЛИТЕРАТУРЫ........................................................................ 47

Приложение 1........................................................................................... 48

Приложение 3........................................................................................... 50

Приложение 4........................................................................................... 52