Определение отметок точек местности по горизонталям

а) Точка лежит на горизонтали.
В этом случае отметка точки равна отметке горизонтали (см. рис. 35): H_А = 75 м; Н_С = 55 м.

б) Точка лежит на скате между горизонталями.
Если точка лежит между горизонталями, то через нее проводят кратчайшее заложение, масштабной линейкой измеряют длину отрезков а и b (см. рис. 35, точка В) и подставляют в выражение

где h – высота сечения рельефа. Если точка лежит между горизонталью и полугоризонталью, то вместо h в формулу подставляют 0,5h.

Рис. 35. Решение задач на карте с горизонталями

Определение крутизны ската

Крутизна ската по направлению заложения определяется двумя показателями – уклоном и углом наклона по формуле

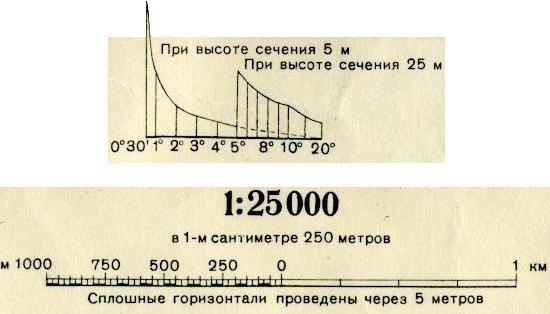
Следовательно, тангенс угла наклона линии к горизонту называется её уклоном. Уклон выражают в тысячных – промиллях (‰) или в процентах (%). Например: i = 0,020 = 20‰ = 2%.

Для графического определения углов наклона по заданному значению заложения d, масштабу М и высоте сечения рельефа h строят график заложений (см. рис. 36).

Вдоль прямой линии основания графика намечают точки, соответствующие значениям углов наклона. От этих точек перпендикулярно к основанию графика откладывают в масштабе карты отрезки, равные соответствующим заложениям, а именно

Концы этих отрезков соединяют плавной кривой (см. рис. 36).

Заложение линии, угол наклона которой надо определить, снимают с карты при помощи измерителя, а затем, укладывая на графике между основанием и кривой измеренный отрезок, находят соответствующее ему значение угла наклона.

Рис. 36. График заложений для углов наклона

Аналогично строят и пользуются графиком заложений для уклонов (рис. 37).

Рис. 37. График заложений для уклонов

Построение линии с заданным уклоном

Задача построения линии с заданным уклоном решается в проектировании трасс железных, автомобильных и других линейных сооружений. Она заключается в том, что из некоторой точки, обозначенной на карте, необходимо провести линию с заданным уклоном i по заданному направлению. Для этого сначала определяют значение заложения d, соответствующее заданным i и h. Его находят по графику заложения уклонов или вычисляют по формуле

d = h/i.

Далее, установив раствор измерителя равным полученному значению d, ставят одну его ножку в начальную точку K, а другой засекают ближайшую горизонталь и тем намечают точку трассы, из которой в свою очередь засекают следующую горизонталь, и т.д. (см. рис. 38).

Рис. 38. Построение линии с заданным уклоном

Построение профиля по топографической карте

Профилем местности называют уменьшенное изображение вертикального разреза местности по заданному направлению.

Пусть требуется построить профиль местности по линии DE, указанной на карте (рис. 39). Для построения профиля на листе бумаги (как правило, используется миллиметровая бумага) проводят горизонтальную прямую и на ней, обычно в масштабе карты (плана), откладывают линию DE и точки её пересечения с горизонталями и полугоризонталями. Далее из этих точек по перпендикулярам откладывают отметки соответствующих горизонталей (на рис. 39 это отметки 50, 55, 60, 65, 70, 75, 80 и 82,5 м). Чтобы отобразить профиль более рельефно, отметки точек обычно откладывают в масштабе в 10 раз крупнее масштаба плана. Соединив прямыми концы перпендикуляров, получают профиль по линии DE.

Рис. 38. Построение профиля по топографической карте

 

Вопросы для самоконтроля

1. Что понимают под рельефом местности?

2. Назовите формы рельефа.

3. Что такое горизонталь? Назовите её основные свойства.

4. Что такое высота сечения рельефа?

5. Что называется заложением горизонталей?

6. Что такое уклон линии?

7. Как определяется нормальная высота сечения рельефа?

8. Как определить на карте высоту точки и крутизну ската линии?

9. Что представляет собой цифровая модель местности и электронная карта?

10. Какие исходные данные необходимы для создания цифровых моделей местности?

11. Как классифицируются цифровые модели местности по способу размещения исходной информации и правил ее обработки на ЭВМ?