
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Искусственные формы рельефа изображают горизонталями чёрного цвета с соответствующей оцифровкой горизонталей.Содержание книги
Поиск на нашем сайте
Степень наклона местности определяется крутизной скатов или уклоном местности. Крутизна ската (рисунок 10) - угол наклона
В
Секущие плоскости h (высота сечения)
d (заложение)
Рисунок 10 - Крутизна ската и уклон линии местности Крутизна ската (склона) местности может быть определена из выражения
Уклон линии местности i – отношение заложения h к горизонтальному проложению d i = h / d = tg
Уклон i выражают десятичной дробью, в процентах (о/о) или промиле (о/оо). Например, уклон i = 0.015 или 1.5 о/о, или 15 о/оо. Кроме горизонталей, рельеф изображается масштабными и внемасштабными условными знаками и дополняется различными цифровыми характеристиками, что позволяет изображать рельеф местности в полном объёме.
4. Задачи, решаемые на картах и планах
На картах и планах решаются задачи определения прямоугольных и географических координат, измерение расстояний, углов ориентирования, уклонов и углов наклона, решение обратных геодезических задач и другие. Остановимся на рассмотрении некоторых из них.
а). Измерение на карте углов ориентирования
Ориентировать линию на местности – значит определить её положение относительно другого направления, принятого за исходное. В качестве исходных в геодезии используют следующие направления (рисунок 11): - северное направление истинного меридиана; - северное направление осевого меридиана Х 0; - северное направление магнитного меридиана; Углы ориентирования, измеряемые относительно перечисленных исходных направлений называют соответственно истинным азимутом Аи, дирекционным углом Ист. мерид.Линия сетки Магнитн. мерид.
- -
Аи А В
Рисунок 11 - Углы ориентирования
Угол Угол
Значения магнитного склонения и сближения меридианов подписываются под южной рамкой карты. При необходимости сближение меридианов нов может быть вычислено по формуле
где
Между истинным, магнитным азимутами и дирекционным углом существует определённая математическая зависимость. Из рисунка 11 нетрудно заметить, что
А и =
А и = А м + (
Приравняв правые части равенства, получим
А м =
А
Рисунок 12 - Прямые и обратные направления (дирекционные углы, азимуты направлений) Соответственно и дирекционные углы и азимуты направлений бывают прямыми и обратными: Зависимость между прямым и обратным дирекционными углами выражается соотношением
На практике при решении различных задач часто используются не дирекционные углы, а румбы. Румбом направления r называют острый угол в пределах 900 в одной из четвертей между ближайшим северным или южным меридианом (вертикальной линией сетки) и данным направлением. При обозначение румба указывают четверть, а затем угловую величину в градусной мере. Например, для первой четверти - СВ: 450 35 ', для второй - ЮВ: 650 37 '; для третьей ЮЗ: 420 35 ' ; для четвёртой - СЗ: 570 51 ' Румбы и дирекционные углы (азимуты) направлений могут быть представлены в виде рисунка 13. С
r1V r1
З 1V 1 В 111
r111 r11
Ю
Рисунок 13 - Зависимость между румбом и дирекционным углом
Из приведенного рисунка нетрудно вывести и соотношения, представляющие собой зависимость между дирекционным углом (азимутом) направления и румбом (таблица 1).
Таблица 1 - Соотношения между румбами и дирекционными углами
Значения дирекционных углов и румбов измеряются по карте, если провести в данной точке исходное направление. Дирекционные углы измеряются с помощью транспортира, устанавливаемого в точке пересечения данного направления с вертикальной линией сетки или линией ей параллельной, относительно северного направления вертикальной линии сетки от 00 до 3600, а румбы – от 00 до 900 относительно северного или южного направлений вертикальной линии сетки. На рисунке 14 а,б показаны примеры измерения по карте дирекционного угла и румба. а) Измерение дирекционного угла б) Измерение румба
В
А
Рисунок 14 - Измерения по карте дирекционного угла и румба
б) Решение обратной геодезической задачи
Сущность решения задачи заключается в определении по прямоугольным координатам двух точек расстояния между ними и дирекционного угла направления с одной точки на другую (рисунок 15). Х
В
А У
Рисунок 15 - Решение обратной геодезической задачи
Из треугольника АВС d2 АВ =
В общем случае для нахождения дирекционного угла направления необходимо определить румб направления по аналогичной формуле
rАВ = arc tg (±
затем по знакам Вычислив румб r и дирекционный угол
d = (±
в). Измерение площадей по карте
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.167 (0.013 с.) |

 0 ската АВ к горизонтальной плоскости. На данном рисунке d - заложение ската, т.е. проекция ската АВ на плоскость. Угол
0 ската АВ к горизонтальной плоскости. На данном рисунке d - заложение ската, т.е. проекция ската АВ на плоскость. Угол 
 i
i


 +
+  +
+ 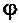 (
( -
- 
 Направления могут быть прямыми и обратными. У линии АВ (рисунок 12) направление с точки А на точку В называют прямым, а с точки В к на точку А – обратным.
Направления могут быть прямыми и обратными. У линии АВ (рисунок 12) направление с точки А на точку В называют прямым, а с точки В к на точку А – обратным.
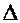 Х
Х










