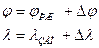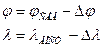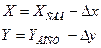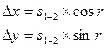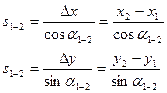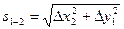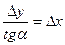Расчетно-графическая работа № 2

Определение географических и прямоугольных координат точек и ориентирных углов направлений по карте.

 

Цель работы: научиться определять географические и прямоугольные координаты по топографической карте. Определить дирекционный угол и географический азимут направлений по топографической карте.

 

Общие сведения

Географические координаты заданной точки определяются следующим способом. На листе карты, соединяя одноименные значения интервалов минутной рамки, проводят по выверенной линейке ближайшие к заданной точке линии южной параллели и западного меридиана. После чего определяют их градусную величину. Географические координаты заданной точки определяют по формулам:

где, Δφ и Δλ – приращения координат точки до линий с известными значениями географических координат.

Для определения приращений координат, с помощью циркуля-измерителя и масштабной линейки по карте определяют отрезки Δa и Δb, а по минутной рамке определяют расстояния a и b, соответствующие определенным интервалам минут или секунд по широте и долготе. Приращения координат определяют по формулам:

где, а – размер минуты по широте в мм;

b – размер минуты по долготе в мм.

Например, для точки 1 (рис. 4.1.) широта ближайшей южной параллели φ_ЮЖ=54°41', долгота западного меридиана λ_ЗАП=18°02'.

Для контроля определения координат на карте проводят ближайшие к заданной точке линии северной параллели и восточного меридиана. После аналогичных измерений географические координаты вычисляют по формулам:

Расхождение между двумя определениями не должно превышать 0,1''.

Рис. 4.1. Определение географических координат

по топографической карте

 

Прямоугольные координаты точек определяют на основе линий координатной сетки (рис. 4.1.). Первоначально координаты юго-западного угла, в котором находится заданная точка, выражая их значения в метрах. Из заданной точки опускают перпендикуляры на южную и западную стороны квадрата и измеряют их длину в масштабе карты или плана, получая таким образом значения приращений координат Δх и Δу. Прямоугольные координаты вычисляют по формулам:

 

Например, для точки 2, Х_ЮЖ=6 067 000 м и У_ЗАП=4 311 000 м. Контроль осуществляют путем аналогичного измерения приращений от данной точки до северной и восточной сторон квадрата по формулам:

 

Если расхождение не превышает величины 3 М 10^-4, то за окончательный результат принимают среднее арифметическое значение.

 

 

Рис. 4.2. Определение прямоугольных координат

по топографической карте

 

Дирекционный угол измеряют по ходу часовой стрелки от северного направления линии, параллельной оси абсцисс, до направления заданной линии (рис. 4.3.). Для измерения дирекционного угла заданное направление продолжают до пересечения с одной из линий координатной сетки, расположенной слева от начальной точки, когда дирекционный угол меньше 180°, или справа, когда он больше.

Географический азимут измеряют по ходу часовой стрелки от северного направления географического меридиана, проходящего через начальную точку заданной линии (рис. 4.3). Величину азимута определяют так же как при измерении дирекционных углов.

 

Задание

Определить географические и прямоугольные координаты вершин полигона по учебной карте. Определить дирекционные углы и географические азимуты сторон полигона, вычислить их магнитные азимуты.

 

Порядок выполнения работы

В соответствии с полученным заданием, по учебной карте определить географические и прямоугольные координаты вершин полигона. Измерить транспортиром дирекционные углы и географические азимуты сторон полигона, вычислить их магнитные азимуты (прил. 3).

 

 

 

Рис. 4.3. Измерение дирекционных углов и географических азимутов линий

по топографической карте

 

Прямая и обратная геодезическая задача.

 

Цель работы: научиться решать прямую и обратную геодезические задачи на плоскости.

 

Общие сведения

Прямая геодезическая задача – состоит в том, чтобы определить координаты конечной точки Х₂, У₂ по известным координатам начальной точки Х₁, У₁, горизонтальному проложению s_1-2 и дирекционному углу α_1-2.

Рассмотрим наиболее простой случай, когда горизонтальное проложение АВ находится в I четверти, и имеет северо-восточное направление и румб линии равен значению дирекционного угла (рис. 5.1.).

Приращение координат линии – ортогональная проекция горизонтального проложения этой линии на оси ординат, их обозначают Δх и Δу:

тогда,

Приращения координат могут быть вычислены по дирекционному углу линии и ее горизонтальному проложению, являющемуся гипотенузой прямоугольного треугольника, в котором катеты – приращения координат и вычисляются по формулам:

Приращения координат имеют знаки, плюс или минус, в зависимости от знака косинуса или синуса дирекционного угла. При переходе от дирекционных углов к румбам:

В связи с тем, что значения тригонометрических функция всегда положительны cos r и sin r, т.к. r ≤ 90°, знаки приращений координат определяют в соответствии с названиями румбов.

Обратная геодезическая задача – состоит в том, чтобы вычислить горизонтальное проложение s_1-2 и дирекционный угол α_1-2 по известным координатам начальной (Х₁, У₁) и конечной (Х₂, У₂ ) точек.

Рис. 5.1. Схема решения прямой и обратной

геодезических задач на плоскости.

 

По катетам прямоугольного треугольника, т.е. приращениям координат можно вычислить дирекционный угол:

тогда,

Горизонтальное проложение s_1-2 вычисляют по формулам:

Эту же задачу можно решить другим способом:

Искомый дирекционный угол α_1-2 вычисляется по формулам:

 

Задание

1. Определить прямоугольные координаты точки В, если координаты точки А, х_А=6 163 173, 43 м, у_А=9 492 631, 12 м, α_АВ=318°47', s_AB=673,56 м.

2. Вычислить дирекционный угол α_CD и горизонтальное проложение s_CD, если прямоугольные координаты точек C и D составляют х_C= 6 319 281,1м, у_C=9 540 014,2 м, x_D=6 323 061,6 м, y_D=9 542 229,7 м.

 

Порядок выполнения работы

Задание 1. При решении прямой геодезической задачи значения приращений координат можно вычислить при помощи таблиц натуральных значений тригонометрических функций.

При решении прямой геодезической задачи с использованием таблиц натуральных значений тригонометрических функций сначала записывают исходные данные α_АВ (п/п 1), s_АВ (п/п 2), x_А (п/п 3), y_А (п/п 4) (табл. 5.2). Затем из таблиц натуральных значений тригонометрических функций находят значение cos α_АВ и sin α_АВ. Далее вычисляют Δx_АВ и Δy_АВ, отрицательный знак зависит от sin 318°47' (IV четверть). Далее придавая к координатам точки А приращения координат вычисляют координаты точки В.

 

Рабочие формулы:

Таблица 5.2.

Решение прямой геодезической задачи.

Значение дирекционного угла и длина линии	ΔХАВ	ΔУАВ
п/п	Обозна-чения	Вычисления	п/п	Обозна-чения	Вычисле-ния	п/п	Обозна-чения	Вычисле-ния
	αАВ	318°47'		cos αАВ	+0,75237		sin αАВ	-0,65873
	sАВ	673, 56 м		ΔxАВ	+506,77		ΔyАВ	-443,69 м
				xА	63 173,43м		yА	92 631,12 м
				xВ	63 680,20 м		yВ	92 187,43 м

 

Для контроля вычисленных приращений пользуются формулой:

Допустимые отклонения составляют 0,01-0,02 м.

 

2. При решении обратной геодезической задачи при помощи таблиц натуральных значений тригонометрических функций сначала выписывают координаты исходных пунктов (табл. 5.3.).

Рабочие формулы:

 

Таблица 5.3.

Решение обратной геодезической задачи

п/п	Обозна-чения	Вычисле-ния	п/п	Обозна-чения	Вычисления	п/п	Обозна-чения	Вычисления
	yD	9 542 229,7		xD	6 323 061,6		tg αCD	+0,58728
	yC	40 014,2		xC	19 289,1		rCD	CB: 30°25'29''
	yD– yC	+2 215,5		xD– xC	+3 772,5		αCD	30°25'29''
	sin αCD	0,50640		cos αCD	0,86229
	sCD	4 374.95		sCD	4 374,94		sCD ср	4 374,94

 

Затем вычисляют разности координат и определяют значение tgα. Пользуясь таблицами натуральных значений тригонометрических функций и учитывая знаки приращений координат, по величине tgα вначале определяют румб искомого направления, а затем и дирекционный угол.

Далее определив значения sin α и cos α дважды вычисляют значения искомой стороны, как частное от деления (п/п 5 и п/п 10) и (п/п 6 и п/п 11). Расхождение должно быть не более одной единицы пятого знака. Среднее значение из двух делений принимается за окончательное.

Таблица 5.4.

Контрольные задания для самостоятельной работы

№ варианта	прямая геодезическая задача	обратная геодезическая задача
координаты исходного пункта	дирек-ционный угол α1-2	горизон-тальное проложе-ние s1-2 , м	координаты исходных пунктов
Х	У	Х	У	Х	У
	6 134 629,3	9 416 014,3	266°24'	528,46	6 131 975,2	9 415 881,6	6 132 215,2	9 413 215,1
	6 233 952,4	9 573 914,8	293°02'	386,79	6 133 952,4	9 413 914,8	6 134 629,3	9 416 014,3
	6 163 952,5	9 163 914,8	283°01'	967,57	6 233 517,2	9 575 025,7	6 233 952,4	9 573 914,8
	6 131 421,3	9 514 701,6	227°30'	794,65	6 133 517,2	9 485 025,7	6 131 421,3	9 484 701,6
	6 131 975,2	9 415 881,6	38°57'	697,62	6 161 421,3	9 514 701,6	6 163 952,5	9 163 914,8
	6 133 952,4	9 413 914,8	111°14'	625,87	6 133 415,9	9 517 608,2	6 131 421,3	9 514 701,6
	6 134 629,3	9 416 014,3	192°47'	628,76	6 131 975,2	9 415 881,6	6 132 215,2	9 413 215,1
	6 233 952,4	9 573 914,8	81°42'	475,46	6 133 952,4	9 413 914,8	6 134 629,3	9 416 014,3
	6 163 952,5	9 163 914,8	266°24'	528,46	6 233 517,2	9 575 025,7	6 233 952,4	9 573 914,8
	6 131 421,3	9 514 701,6	293°02'	386,79	6 133 517,2	9 485 025,7	6 131 421,3	9 484 701,6
	6 131 975,2	9 415 881,6	283°01'	967,57	6 161 421,3	9 514 701,6	6 163 952,5	9 163 914,8
	6 133 952,4	9 413 914,8	227°30'	794,65	6 133 415,9	9 517 608,2	6 131 421,3	9 514 701,6

 

 

6. Основные формы рельефа. Задачи решаемые на топографических картах и планах.

 

Цель работы: научиться определять отметки точек по топографической карте, вычислять превышения, уклоны. Строить продольный профиль.

Общие сведения

Рельеф местности – совокупность различных по форме неровностей (понижений и повышений) на физической поверхности Земли. В зависимости от абсолютного значения высот местности различают: равнинную, холмистую и горную местность.

Горная местность – представляет собой систему прямолинейных или дугообразных горных цепей высотой 500 м и выше над уровнем моря.

Холмистая местность – представляет собой резко выраженное чередование возвышенностей и понижений с разностью высот до 200 м.

Равнинная местность – представляет собой горизонтальную или с небольшим наклоном плоскую поверхность Земли, имеет слабовыраженные формы рельефа.

Основные формы рельефа: гора, котловина, лощина, хребет, седловина.

Гора – это возвышенность конусообразной формы, наивысшая точка которой называется вершиной. Вершина в виде площадки – плато, остроконечной формы – пик. Боковая поверхность состоит из скатов, линия их слияний с окружающей местностью – подошва, или основание, горы. Ее разновидности: курган, холм, бугор, сопка и т.д.

Рис. 6.1. Основные формы рельефа (по Покладу, Гридневу, 2007):

а – холм; б – котловина; в – хребет; г – лощина; д –.овраг; е – седловина

 

Котловина – углубление в виде чаши. Самая низкая точка котловины – дно. Боковая поверхность состоит из скатов, линия слияния их с окружающей местностью – бровка.

Хребет – возвышенность, постепенно понижающаяся в одном направлении и имеющая два крутых ската, называемых склонами. Ось хребта между двумя склонами называется водораздельной линией или водоразделом. Если склоны хребта пересекаются под острым углом, то такой водораздел называют гребнем.

Лощина – вытянутое углубление местности, постепенно понижающееся в одном направлении. Ось лощины между двумя скатами называется водосливной линией или тальвегом. Разновидности лощины: долина – широкая лощина с пологими склонами; овраг – узкая лощина с почти отвесными склонами; промоина – узкое углубление с крутыми, обнаженными склонами, образующимися под действием воды; балка – заросший овраг.

Терраса (уступ)– ровная, почти горизонтальная площадка на скате хребта или горы.

Седловина – пониженная часть водораздела, расположенная между двумя смежными вершинами и между двумя лощинами, расходящимися в противоположные стороны.

Характерные точки рельефа – вершина горы, дно котловины, самая низкая точка седловины.

Характерные линии рельефа – водораздел и тальвег.

Горизонталь – кривая линия на плане, все точки которой имеют равные отметки на местности. Основные свойства горизонталей: 1) все точки местности, лежащие на одной горизонтали, имеют равные отметки; 2) горизонтали не могут пересекаться на плане, т.к. лежат на разных высотах (исключение – горные районы, когда изображают нависший утес; 3) горизонтали являются непрерывными замкнутыми линиями.

Высота сечения рельефа – расстояние между горизонталями по высоте.

Заложение – расстояние между горизонталями в плане или карте.