Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие принадлежности точки плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
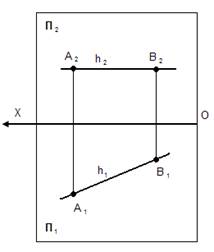
Лекция 1 Начертательная геометрия изучает методы проецирования пространственных форм на плоскость. 1.1. Методы проецирования. 1. Центральное проецирование (все проецирующие лучи выходят из одной точки, перспективное проецирование); 2. Параллельное проецирование (все проецирующие лучи параллельны друг другу): - ортогональное (проецирующие лучи перпендикулярны к плоскости проекции);
Центральное проецирование Параллельное ортогональное проецирование
1.2. Точка. Четверти пространства.
Плоскости проекций:
∏1 – горизонтальная плоскость
∏2 – фронтальная плоскость
∏3 – профильная плоскость
П1 ┴ П2 ┴ П3
I, II, III, IV – четверти пространства
Аксонометрическая модель
Эпюр Монжа.
А1 – горизонтальная проекция точки А
А2 – фронтальная проекция точки А
А3 – профильная проекция точки А
1.3. Прямая. Классификация прямых.
В самом общем случае проекция прямой также прямая линия.
Положение прямой относительно плоскостей проекции.
2. Прямые проецирующие (перпендикулярны какой-либо плоскости проекции);
В) профильно-проецирующие (перпендикулярны П3).
3. Прямые уровня (параллельны какой-либо плоскости проекции); А) горизонтальная прямая уровня (параллельна П1, но неперпендикулярна П2 и П3);
h – горизонтальная прямая уровня (горизонталь)
Б) фронтальная прямая уровня (параллельна П2, но неперпендикулярна П1 и П3);
f – фронтальная прямая уровня (фронталь)
В) профильная прямая уровня (параллельна П3, но неперпендикулярна П1 и П2).
р – профильная прямая уровня
1.4. Взаимное расположение прямых в пространстве.
В пространстве прямые могут быть: 1. Параллельны;
a1║b1 a║b a2║b2
2. Пересекающиеся; Если прямые в пространстве пересекаются, то на эпюре точки пересечения одноимённых проекций лежат на одной линии связи.
a1 ∩ b1 = K1 a ∩ b a2 ∩ b2 = K2
На эпюре одноименные проекции скрещивающихся прямых пересекаются. Точки пересечения проекций скрещивающихся прямых не лежат на одной линии связи – точки мнимого пересечения. Эти точки используют для определения видимости и называют конкурирующими.
Точки 1 и 2 конкурируют по глубине (точка 1 глубже и на П2 закрывает точку 2). Y (2) < Y (1) Точки 3 и 4 конкурируют по высоте (точка 4 выше и на П1 закрывает точку 3). Z (3) < Z (4)
Если точка принадлежит прямой, то на эпюре одноименные проекции этой точки принадлежат одноименным проекциям этой прямой.
Точка А принадлежит прямой a Точка В не принадлежит прямой а
‖ 1.6. Правило проецирования прямого угла.
В самом общем случае прямой угол проецируется с искажением. Если одна сторона прямого угла является прямой уровня (т.е. параллельна какой-либо плоскости проекции), а другая сторона неперпендикулярна этой плоскости проекции, то на нее прямой угол проецируется в Н.В.
1.7. Следы прямой.
Следом прямой называется точка пересечения заданной прямой с плоскостью проекции. 1. Для того чтобы построить горизонтальный след, необходимо продолжить фронтальную проекцию прямой до пересечения с осью, затем опустить перпендикуляр до пересечения с горизонтальной проекцией прямой. 2. Для того чтобы построить фронтальный след прямой, необходимо продолжить горизонтальную проекцию прямой до пересечения с осью, затем восстановить перпендикуляр до пересечения с фронтальной проекцией прямой. М – горизонтальный след М1 – горизонтальная проекция горизонтального следа М2 – фронтальная проекция горизонтального следа N – фронтальный след N1 – горизонтальная проекция фронтального следа
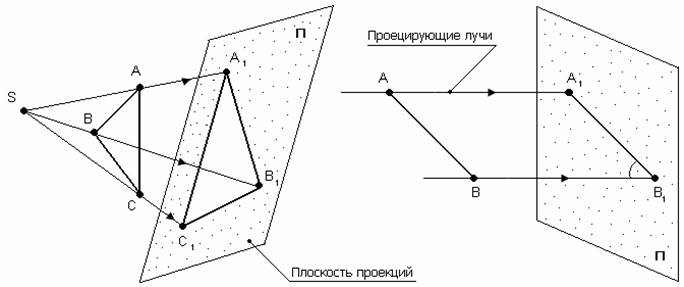
1.8. Определение натуральной величины отрезка прямой. В самом общем случае отрезок проецируется на плоскость с искажением (не в натуральную величину). Исключение: прямые частного положения. Натуральную величину (Н.В.) определяют по правилу прямоугольного треугольника.
Правило прямоугольного треугольника. Для того чтобы определить Н.В. отрезка необходимо:
Гипотенуза А1В0 – Н.В. Гипотенуза A2B0 – Н.В. ∆Z = ZA - ZB ∆Y = YA - YB α – угол наклона [AB] к П1 β – угол наклона [AB] к П2
Лекция 2 2.1. Плоскость.
Способы задания плоскости: 1. Тремя точками, не лежащими на одной прямой; 2. Прямой и точкой вне этой прямой; 3. Двумя пересекающимися прямыми; 4. Двумя параллельными прямыми; 5. Плоской фигурой; 6. Следами (частный случай двух пересекающихся прямых).
След плоскости – прямая пересечения заданной плоскости с плоскостью проекции.
Горизонтальный след плоскости – нулевая горизонталь. h0 = α ∩ П1
Фронтальный след плоскости – нулевая фронталь.
f0 = α ∩ П2
α П1 – горизонтальный след α П2 – фронтальный след αX – точка схода следов
Построение следов плоскости.
Если прямая лежит в плоскости, то ее следы лежат на одноименных следах этой плоскости. Для того чтобы построить след плоскости необходимо построить минимум два следа прямых, лежащих в этой плоскости, а затем соединить их одноименные следы. Прямая и точка в плоскости. Лекция 3 Метрические и позиционные задачи. 3.1. Построение линии пересечения плоскостей. Задача I-го типа. Оба геометрических образа частного положения.
Решение: Проекции результата есть на чертеже и лежат на вырожденных проекциях проецирующих образов (построение не требуется).
Пример: Построить линию пересечения плоскости α с плоскостью β.
α – горизонтально-проецирующая плоскость
β – горизонтальная плоскость уровня
α Ո β = а
Один геометрический образ (ГО) частного положения, имеет вырожденную проекцию, а второй ГО общего положения (нет вырожденных проекций).
Решение: Одна проекция результата есть на чертеже и находиться на вырожденной проекции проецирующего образа (на П1 или П2), а другая определяется из условия принадлежности ко второму не проецирующему образу.
Пример: (АВС) – плоскость общего положения, γ – фронтально-проецирующая плоскость. ∆ АВС Ո γ = 12 1222 принадлежит γ П2
Задача III-го типа. Оба ГО общего положения.
Решение: При помощи посредников. В качестве посредников выбираются ГО частного положения и решение задачи сводится к решению задачи II-го типа. Пример: α – горизонтальная плоскость уровня, плоскость-посредник β – плоскость-посредник
3.2. Построение точки пересечения прямой с плоскостью.
Оба геометрических образа частного положения. Прямая а – фронтально-проецирующая
(ABC) – горизонтально-проецирующая
Проекция результата лежит на вырожденных проекциях проецирующих образов.
K1 – на вырожденной проекции треугольника АВС.
К2 – на вырожденной проекции прямой а. АВС Ո а = К
Плоскость задана следами. Один ГО общего положения, второй частного положения.
α – плоскость общего положения.
Прямая а – горизонтально-проецирующая.
Горизонтальная проекция результата точка К1 лежит на вырожденной проекции прямой а, фронтальная проекция точки К2 определяется из условия принадлежности ко второму не проецирующему образу плоскости α.
α Ո а = К
Задача III-го типа. Оба ГО общего положения. Решаем при помощи посредника (плоскости частного положения). 1. Вводим плоскость-посредник β (β – частного положения и проходит через прямую а); 2. Определяем линию пересечения плоскости (АВС) – общего положения и плоскости β – частного положения. Решаем задачу II-го типа; 3. Выделяем искомую точку К как точку пересечения заданной прямой и линии пересечения плоскостей [1 - 2];
На эпюре:
2. (АВС) ∩ β = [1 - 2] Решаем задачу II-го типа;
3. а ∩ [1 - 2] = К.
Лекция 4 Взаимно-параллельные и взаимно-перпендикулярные прямые и плоскости. 4.1. Построение прямой параллельной плоскости. Для того чтобы провести через точку А прямую параллельную плоскости α необходимо: 1) в плоскости α выбрать или построить произвольную прямую; 2) через точку А провести новую прямую параллельную выбранной прямой.
a║ α a1║M1N1
Для того чтобы проверить, параллельна ли прямая плоскости необходимо попытаться в заданной плоскости построить прямую параллельную заданной. Если это удастся, то прямая и плоскость параллельны.
4.2. Построение параллельных плоскостей. Для того чтобы через точку А провести плоскость параллельную заданной необходимо в заданной плоскости провести две произвольные пересекающиеся прямые и через точку А провести новые прямые, соответственно параллельные выделенным (удобнее всего использовать прямые частного положения – горизонтали и фронтали).
Для того чтобы проверить параллельны ли две плоскости необходимо попытаться построить в этих плоскостях пересекающиеся прямые, которые были бы попарно параллельны.
α ║β h2║h2I h1║h1I
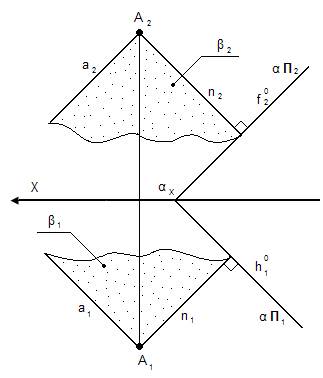
4.3. Построение прямой перпендикулярной плоскости.
4.4. Построение взаимно-перпендикулярных плоскостей. Для того чтобы через точку А провести плоскость перпендикулярную заданной необходимо сначала построить прямую перпендикулярную заданной плоскости, а затем через эту прямую провести новую плоскость (решений бесконечное множество).
n – нормаль (перпендикуляр)
n ┴ α
α ┴ β n1 ┴ f10
Для того чтобы проверить перпендикулярны ли заданные плоскости необходимо в одной плоскости попытаться найти или построить перпендикуляр к другой.
n2 ┴ β П2
Лекция 5 Способы преобразования проекций.
Цель преобразований: ГО общего положения путем преобразования проекции привести к частному положению для упрощения решения метрических задач (нахождение площади, расстояния, углов).
Способ вращения. Сущность способа: При неизменном положении системы плоскостей проекции П1 и П2 в пространстве ГО меняет свое положение так, что каждая его точка перемещается по окружности, расположенной в плоскости вращения перпендикулярно выбранной оси вращения. Лекция 6 6.1. Вращение точки. — 1. Вращение вокруг проецирующей оси (i – ось);
Задача:
Прямую общего положения преобразовать в проецирующую вращением вокруг проецирующей оси.
Решение:
1) Прямую общего положения преобразуем в прямую уровня. Для этого горизонтальную проекцию располагаем параллельно оси (i перпендикулярна П1, проходит через точку B); 2) Прямую уровня АIB преобразуем в проецирующую.
— 2. Плоскопараллельное перемещение – вращение вокруг проецирующей оси, без указания оси вращения (представляем ее, не показываем на чертеже). Сущность способа:
Плоскости проекций своего положения не меняют (П1 и П2 на месте), меняет положение ГО так, что каждая его точка совершает движение по окружности, расположенной в плоскости вращения, перпендикулярной оси вращения. Задача: Преобразовать плоскость общего положения в плоскость уровня.
Решение:
1) Плоскость АВС преобразуем в проецирующую, перпендикулярную П2. Для этого в плоскости АВС проводим горизонталь, которую поворачиваем до положения фронтально-проецирующей прямой, а вместе с ней и весь треугольник АВС (вокруг горизонтально-проецирующей оси, которую не указываем); Все точки АВС в пространстве переместились по окружности, а на эпюре переместились фронтальные проекции 2) Проецирующую плоскость АIBICI преобразуем в плоскость уровня AIIBIICII. Для этого вращаем треугольник вокруг фронтально-проецирующей оси, а его проекцию (фронтальную) до положения параллельного оси ОХ.
AIIBIICII ║ Х
— 3. Совмещение. Вращение вокруг линии уровня. Сущность способа Если плоскость вращать вокруг ее следа до совмещения с плоскостью проекций, в которой расположен этот след, то отрезки, линии и фигуры, расположенные в плоскости, изобразятся без искажен
Вращение вокруг линии уровня.
Лекция 7 Многогранники. 7.1. Многогранные поверхности. Многогранной называется поверхность, образованная отсеками (частями) пересекающихся плоскостей.
Многогранник – замкнутая многогранная поверхность.
Грань – отсек плоскости.
Ребро – линия пересечения граней.
Многогранники
Призмы Пирамиды
Призма – многогранник, у которого боковые рёбра параллельны основанию. А) Прямая (боковые рёбра перпендикулярны основанию); Б) Наклонная (боковые рёбра под наклоном к основанию).
Пирамида – многогранник, боковые рёбра которого пересекаются в одной точке (всегда образ общего положения).
Правильные многогранники – многогранники, грани которых являются правильными многоугольниками (куб: грань – квадрат, тетраэдр: грань – правильный треугольник).
7.2. Пересечение многогранника плоскостью. Позиционные задачи. Сечение многогранника плоскостью – многоугольник. Стороны этого многоугольника – прямые пересечения многогранника с заданной плоскостью. Вершины многоугольника – точки встречи рёбер с секущей плоскостью. Задача I-го типа. Прямая призма – проецирующий образ, имеет вырожденную проекцию.
Обычно есть необходимость определить Н.В. фигуры сечения. В данном случае Н.В. треугольника 123 находим способом плоскопараллельного перемещения.
β П1, βI П1, βII П1 – плоскости вращения.
Преобразовали проецирующую плоскость в плоскость уровня.
Задача II-го типа. Пирамида – всегда непроецирующий образ (общего положения).
А) Пирамида (плоскость α фронтально-проецирующая);
Б) Призма проецирующая (плоскость общего положения).
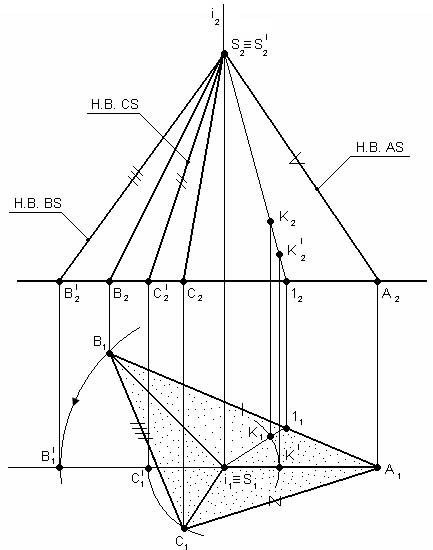
Задача III-го типа. Решение задачи сводится к определению точек пересечения рёбер пирамиды с заданной плоскостью, т.е. к нахождению точки встречи прямой с плоскостью.
Последовательно заключаем каждое боковое ребро во вспомогательную плоскость-посредник. Таким образом, сводим задачу к задачe II-го типа.
1. Заключаем ребро AS в плоскость-посредник (σ – фронтальная плоскость уровня), σ ∩ α по фронтали;
2. Ребро BS заключаем во фронтально-проецирующую плоскость β;
3. Для нахождения точки 3 строим линию пересечения плоскостей α и стороны треугольника АСS. Одна общая точка 1 построена, а другая находится на пересечении прямой АС и следа точки F на П1. Соединяем точки f2 и F2 – получаем проекцию пересечения плоскостей.
Построение точек входа и выхода.
Оба образа проецирующие. Проекции результата находятся на вырожденных проекциях геометрических образов.
Точки пересечения прямой с многогранником – точки 1 и 2 – точки входа и выхода.
Призма – фронтально-проецирующая, прямая а – общего положения.
1 – точка входа
2 – точка выхода
1. Заключаем прямую а во фронтально-проецирующую плоскость-посредник α; 2. Строим фигуру сечения пирамиды плоскостью α. Решаем задачу II-го типа; 3. Выделяем искомые точки входа и выхода как точки пересечения заданной прямой с контуром фигуры сечения пирамиды плоскостью-посредником α.
Точка L – точка входа
Точка К – точка выхода
7.4. Пересечение многогранников между собой.
Задача I-го типа.
Задача III-го типа.
Алгоритм решения: Задача решается при помощи посредников. 1. Плоскостью-посредником (могут быть разные, чаще плоскость уровня) рассекаем обе поверхности; 2. Строим фигуры сечения плоскостью-посредником каждую из многогранных поверхностей (чаще многоугольники); 3. Находим общие точки пересечения этих многоугольников, принадлежащим плоскости-посреднику, и каждой из пересекающихся многогранных поверхностей; 4. Соединяем полученные точки с учётом видимости граней и рёбер многогранников.
Лекция 8 Построение развёрток многогранников. Развертка – совмещенная с плоскостью поверхность многогранника без разрывов и смятий. Развёртка многогранной поверхности – плоская фигура, полученная в результате последовательного совмещения всех её граней с плоскостью 8.1 Развёртка пирамиды. Способ триангуляции. Сущность способа заключается в нахождении Н.В. всех рёбер пирамиды и построении на плоскости контуров боковых граней (треугольников), которые последовательно соединяют друг с другом смежными рёбрами. К ним присоединяется основание пирамиды
В данном примере Н.В. рёбер определяем способом вращения вокруг проецирующей оси, которая проходит через вершину пирамиды.
Точка К – произвольная точка.
1. Находим Н.В. каждого из рёбер пирамиды; 2. Строим треугольники на развёртке методом засечек; 3. Основание пирамиды – треугольник АВС на П 1 спроецирован в натуральную величину. Пристраиваем основание к ребру СА.
8.2 Развёртка призмы. Способ нормального сечения.
Сущность способа: 1. Многогранную поверхность пересекают плоскостью, расположенной перпендикулярно рёбрам. 2. Определяют Н.В. фигуры сечения (обычно плоско-параллельным перемещением); 3. На произвольной прямой откладывают отрезки, равные сторонам сечения (как бы растягиваем фигуру сечения в прямую линию);
8.3 Способ раскатки. Сущность способа - вращением вокруг линий уровня (рёбер призмы) последовательно совмещаем все боковые грани призмы в одну плоскость, пристраиваем нижнее и верхнее основания. Для возможности построения развёртки способом раскаткой призма должна располагаться так, чтобы на эпюре: 1. Рёбра были линии уровня; 2. Основание проецировалось в Н.В. Если призма занимает другое положение, то при помощи последовательных преобразований необходимо привести к таким исходным данным. Задача. 1.Ось вращения ребро ААI. Вращаем грань ААIВВI, совмещаем эту грань с плоскость параллельной П2 2.Плоскости вращения α, β; α ┴ ААI, β ┴ ВВI 3.Центр вращения: для точки В– О, для точки ВI – OI 4. R=A1В1= H.B.
Лекция 9 9.1. Кривые поверхности. Кривая поверхность – непрерывное множество последовательных положений линии (называемой образующей),перемещающейся в пространстве по определенному закону вдоль другой линии, называемой направляющей.
Точка на поверхности.
Точка принадлежит поверхности, если она принадлежит линии, лежащей на этой поверхности. Линия принадлежит поверхности, если о каждой ее точке можно однозначно сказать, что они принадлежат поверхности.
Изображение поверхности. На эпюре поверхность изображается при помощи очерковой образующей (очерк) – линии, точки которой являются точками касания проецирующих прямых заданной поверхности.
Классификация поверхностей. 1) По закону движения образующей; 1. С поступательным движением; 2. Поверхности движения; 3. Винтовое движение (вращательно-поступательное движение).
2) По виду образующей; 1. Линейчатые поверхности (образующая прямая); 2. Нелинейчатые поверхности (образующая кривая).
3) По признаку развёртываемости; 1. Развёртываемые (развертка без разрывов и смятий); 2. Неразвёртываемые (например, шар).
Поверхности вращения.
1) С криволинейной образующей; 1. Сфера (окружность вращается вокруг оси, проходящей через центр окружности); 2. Торовая поверхность; 3. Эллипсоид; 4. Параболоид; 5. Гиперболоид (однополосный и двуполосный).
2) Линейчатые поверхности вращения; 1. Прямой круговой конус (образующая – прямая, направляющая – окружность); 2. Цилиндр прямой круговой (направляющая – окружность).
Поверхность вращения – поверхность, образованная вращением линии вокруг неподвижной прямой (оси вращения).
Пересечение поверхности плоскостью.
1) Сфера – всегда окружность; 2) Цилиндр: 1. Секущая плоскость параллельная основанию – окружность; 2. Секущая плоскость непараллельная основанию – эллипс; 3. Секущая плоскость перпендикулярна основанию – прямоугольник.
3) Конус: 1. Секущая плоскость параллельна основанию – окружность; 2. Секущая плоскость проходит через вершину – треугольник; 3. Секущая плоскость под углом к основанию – эллипс; 4. Секущая плоскость перпендикулярна основанию (не через вершину) – гипербола; 5. Секущая плоскость параллельна образующим – парабола.
9.2. Позиционные задачи. Задача I-го типа.
Задача II-го типа.
Задача III-го типа.
Пересечение конуса плоскостью общего положения. 1. Решаем с помощью посредников; 2. Определяем положение большой оси эллипса, она располагается по линии ската секущей плоскости α. Для этого введём вспомогательную плоскость-посредник β, которая рассечёт конус по треугольнику (т.к. проходит через его вершину, а плоскость α по линии ската перпендикулярно горизонтальному следу); 3. Определяем положение малой оси эллипса. Она располагается перпендикулярно большой оси и проходит через ее середину. Для ее нахождения используется плоскость-посредник γ (горизонтально-проецирующая). Она рассекает конус по треугольнику, а плоскость α – по горизонтали. В пересечении треугольника и горизонтали на П2 определяем крайние точки малой оси. 4. Определяем дополнительно характерные точки изменения видимости эллипса. Они расположены на очерковых образующих конуса. Для их нахождения на П2 используем вспомогательную плоскость-посредник σ (фронтальная уровня).
Лекция 10 10.1. Пересечение кривой поверхности с прямой. Задача I-го типа. Задача II-го типа.
Задача III-го типа. Решаем при помощи посредника – плоскость общего положения, которая проходит через вершину конуса и заданную прямую, рассекая конус по треугольнику. В пересечении контуров треугольника с заданной прямой выделяем точки входа и выхода. Плоскость-посредник задаём 2-мя пересекающимися прямыми общего положения, одна из которых – заданная прямая, а другая проходит через вершину S.
Строим горизонтальный след плоскости-посредника (для этого находим горизонтальный след прямых a и b).
1. [ S1 II1 ] ∩ [ M1 P1 ] = F1; [ S1 I1 ] ∩ [ M1 P1 ] = E1; 2. a1 ∩ основание конуса = [ I1 II1 ].
Лекция 11. 11.1. Построение линий пересечения поверхностей. 1. Способ вспомогательных секущих плоскостей; В результате пересечения плоскости-посредника с заданными поверхностями должны получаться простые для построения линии прямые или окружности. Сущность способа: 1. Рассекаем обе поверхности плоскостью; 2. Строим фигуры сечения, состоящие из прямых или окружностей; 3. Находим точки пересечения полученных фигур, которые принадлежат сразу 3-м геометрическим образам (каждой из заданных поверхностей и плоскости-посреднику); 4. Соединяем полученные точки по лекало.
2. Способ вспомогательных секущих сфер; Условия применения: 1. Обе поверхности должны быть поверхностями вращения; 2. Оси вращения поверхностей должны пересекаться; 3. Плоскость, образованная пересекающимися осями должна быть плоскостью уровня;
Сущность способа: 1. Пересекаем обе поверхности вспомогательной секущей сферой, каждая поверхность пересекается сферой по окружности; 2. Пересечением полученных окружностей между собой выделяем общие точки принадлежащие сразу 3-м поверхностям (вспомогательным секущим сферам и обеим заданным поверхностям); 3. Соединяем ряд полученных точек последовательно и получаем искомую линию пересечения.
1) Центр вспомогательных сфер выбираем точкой пересечения осей вращения поверхностей; 2) Радиус сфер выбираем в промежутке от Rmin до Rmax; Rmin – сфера с минимальным радиусом должна вписываться в одну поверхность и пересекать другую; Rmax – от центра О до максимально удалённой опорной точки.
Спецкурс. Лекция 12. 12.1. Проекции с числовыми отметками. Сфера применения: Используется для изображения объектов, горизонтальные размеры которых значительно превосходят вертикальные (топографические поверхности, строительные объекты). Сущность метода: Проекция на горизонтальную плоскость проекции П1 остаётся неизменной, а изображение на фронтальную плоскость проекции заменяется числовым значением элемента относительно уровня условно принятого за нулевой.
12.2. Градуирование отрезка прямой, определение интервала, уклона и заложения. Градуирование – определение на прямой положения точек с целочисленными значениями. Заложение (L) – величина проекции отрезка прямой, измеряемая в единицах масштаба. Интервал (l) – величина проекции отрезка, отметки концов которого отличаются на единицу. Уклон (i) – величина, обратная интервалу.
i = 1/l i = (hВ – hА)/L
12.3. Взаимное расположение прямых. 1. Прямые пересекаются;
Градуируем прямые AB и CD.
Если прямые пересекаются, то на эпюре отметка точки пересечения одинакова для каждой прямой.
2. Прямые параллельны; Признаки параллельности:
1) Параллельные проекции (AB║CD); 2) Имеют одинаковый интервал (l1 = l2); 3) Отметки или возрастают или убывают в одном направлении;
3. Могут скрещиваться; Если прямые скрещиваются, то на эпюре для каждой прямой разные отметки у точки их пересечения.
12.4. Изображение плоскости.
Плоскость в проекциях с числовыми отметками может быть задана: 1. Тремя точками;
2. Двумя параллельными прямыми;
3. Пересекающимися прямыми; 4. Масштабом уклона – проградуированная линия ската (прямая перпендикулярная всем горизонталям плоскости).
12.5. Изображение поверхностей.
Все поверхности изображаются с помощью горизонталей. Горизонталь поверхности – линия, соединяющая точки с одинаковыми отметками, полученными в результате рассечения поверхности горизонтальными плоскостями уровня, расположенными на высоте, различающейся на единицу. | |||||||||||
|
| Поделиться: |

 - косоугольное (проецирующие лучи направлены под углом к плоскости проекции).
- косоугольное (проецирующие лучи направлены под углом к плоскости проекции).

 1. Прямая общего положения (непараллельна и неперпендикулярна ни одной из плоскостей проекции);
1. Прямая общего положения (непараллельна и неперпендикулярна ни одной из плоскостей проекции);
 А) горизонтально-проецирующие (перпендикулярны П1);
А) горизонтально-проецирующие (перпендикулярны П1); Б) фронтально-проецирующие (перпендикулярны П2);
Б) фронтально-проецирующие (перпендикулярны П2);

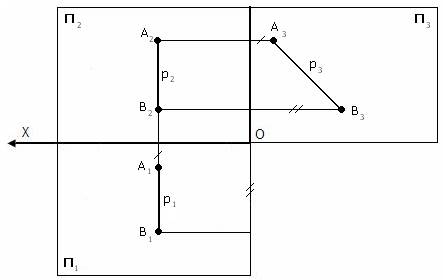
 Если прямые в пространстве параллельны, то на эпюре параллельны их одноимённые проекции.
Если прямые в пространстве параллельны, то на эпюре параллельны их одноимённые проекции.
 3. Скрещивающиеся;
3. Скрещивающиеся; 1.5. Условие принадлежности точки прямой.
1.5. Условие принадлежности точки прямой.
 N2 – фронтальная проекция фронтального следа
N2 – фронтальная проекция фронтального следа построить прямоугольный треугольник, одним катетом которого является одна из проекций отрезка (А1В1 или А2В2), а другим катетом – разность удалений концов отрезка от оси Х, взятая с другой плоскости проекции. Гипотенуза этого треугольника – Н.В. отрезка.
построить прямоугольный треугольник, одним катетом которого является одна из проекций отрезка (А1В1 или А2В2), а другим катетом – разность удалений концов отрезка от оси Х, взятая с другой плоскости проекции. Гипотенуза этого треугольника – Н.В. отрезка.

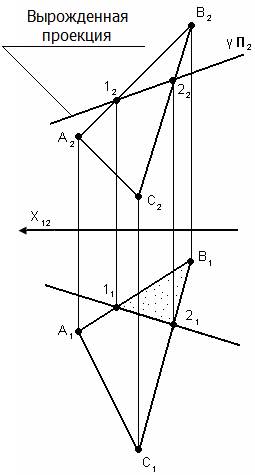 Задача II-го типа.
Задача II-го типа.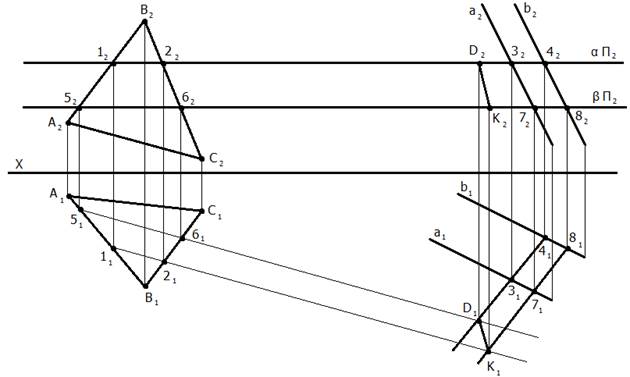
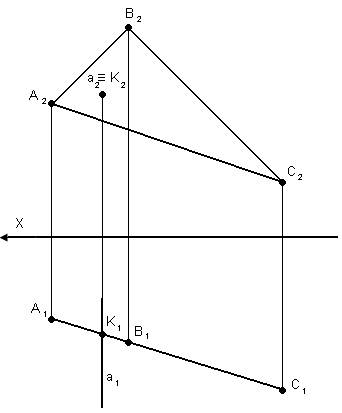 Задача I-го типа.
Задача I-го типа.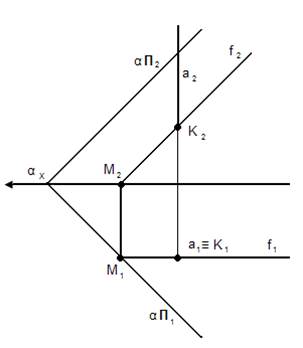 Задача II-го типа.
Задача II-го типа.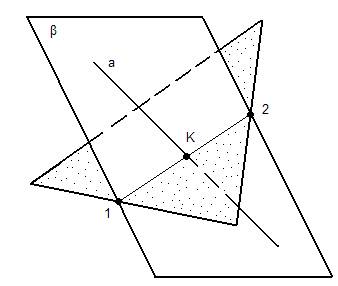 4. Определяем видимость элемента.
4. Определяем видимость элемента.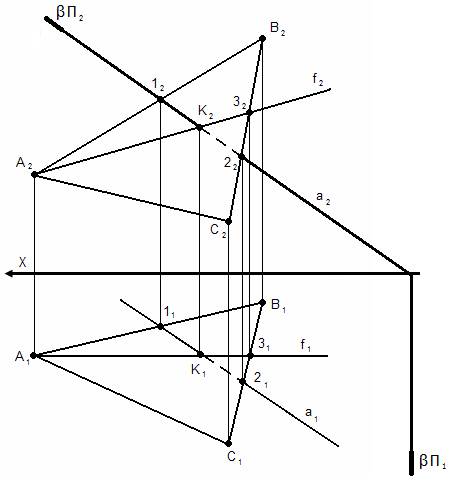 1. Прямая а принадлежит β, β перпендикулярна П2 (через прямую а провели фронтально-проецирующую плоскость β);
1. Прямая а принадлежит β, β перпендикулярна П2 (через прямую а провели фронтально-проецирующую плоскость β);
 a2║M2N2
a2║M2N2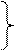 f2║f 2I f1║f 1I
f2║f 2I f1║f 1I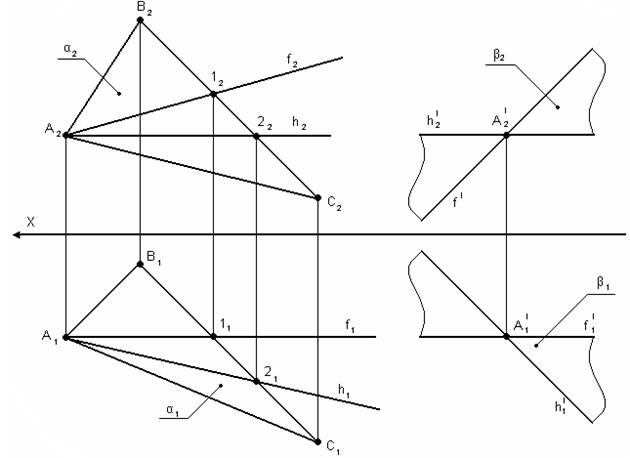
 Для того чтобы через точку А провести прямую перпендикулярную плоскости необходимо фронтальную проекцию прямой направить перпендикулярно фронтальной проекции фронтали плоскости, а горизонтальную проекцию прямой направить перпендикулярно горизонтальной проекции горизонтали плоскости.
Для того чтобы через точку А провести прямую перпендикулярную плоскости необходимо фронтальную проекцию прямой направить перпендикулярно фронтальной проекции фронтали плоскости, а горизонтальную проекцию прямой направить перпендикулярно горизонтальной проекции горизонтали плоскости.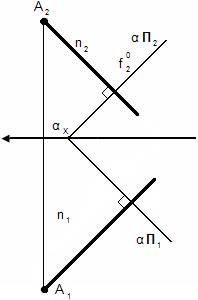
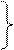 n2 ┴ f20
n2 ┴ f20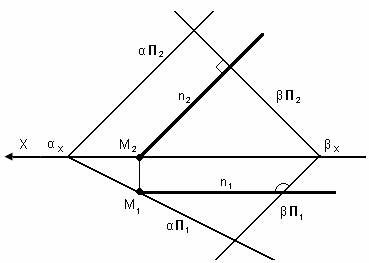
 n1 ┴ β П1
n1 ┴ β П1
 n1 ┴ β β ┴ α
n1 ┴ β β ┴ α При вращении ГО вокруг проецирующей оси на одной проекции все точки перемещаются по окружности (каждая по своей), а другие проекции по прямым параллельным оси, являющимися следами плоскости вращения.
При вращении ГО вокруг проецирующей оси на одной проекции все точки перемещаются по окружности (каждая по своей), а другие проекции по прямым параллельным оси, являющимися следами плоскости вращения.

 Совмещением называется вращение вокруг нулевой горизонтали (вокруг следа плоскости).
Совмещением называется вращение вокруг нулевой горизонтали (вокруг следа плоскости).





 7.3. Пересечение многогранника с прямой линией.
7.3. Пересечение многогранника с прямой линией.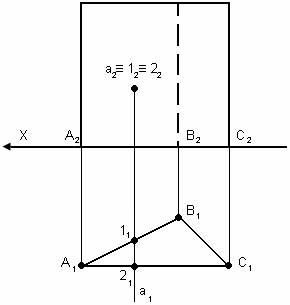 Задача I-го типа.
Задача I-го типа. Задача II-го типа.
Задача II-го типа. Задача III-го типа.
Задача III-го типа.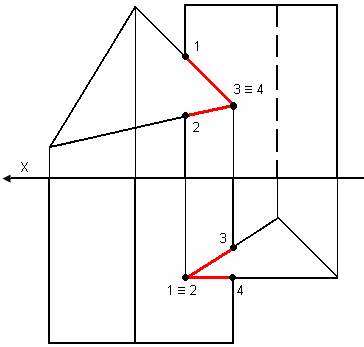
 Задача II-го типа.
Задача II-го типа.


 4. Через вершины проводят прямые, перпендикулярные этому сечению, и на них откладываем Н.В. рёбер призмы вверх и вниз от сечения.
4. Через вершины проводят прямые, перпендикулярные этому сечению, и на них откладываем Н.В. рёбер призмы вверх и вниз от сечения.




 Цилиндр и проецирующая прямая.
Цилиндр и проецирующая прямая.





 Градуирование отрезка с целочисленными отметками концов.
Градуирование отрезка с целочисленными отметками концов. Градуирование отрезка с дробными отметками концов.
Градуирование отрезка с дробными отметками концов.