Комплексный чертеж точки. Абсолютные

Контрольная работа №1

По начертательной геометрии

Она включает 5 комплексных задач. Варианты графических заданий приведены в приложении 1. Всего 20 вариантов: каждая строчка – номер варианта – содержит 5 задач. Таким образом, нумерация задачи 1(4) соответствует первому варианту четвертой контрольной задачи.

Контрольная задача №1

Достроить недостающую проекцию плоскости общего положения j. Найти точку пересечения К прямой m с плоскостью j и определить видимость прямой. Записать координаты точки К отно­сительно точки А. Построить натуральную величину плоской фигуры АВК.

Указания к решению

Задание выполняется на листе чертежной бумаги формата АЗ (297х420). Образец выполнения – рис. 3.

Перед выполнением контрольного задания №1 рекомендуется ответить на вопросы 1 - 21 из приложения 2 и решить задачи 1 – 27 из приложения 3.

Рис. 3

Контрольная задача №2

Построить линию пересечения заданной поверхности проецирующей плоскостью. Определить характер линии сечения и натуральную величину плоской фигуры, полученной в сечении, построить развертку заданной поверхности и нанести на нее линию сечения.

Указания к решению

Задача выполняется на листе формата А3 (297х420).

В левой части формата вычерчивается графи­ческое условие задачи в масштабе 1:1 по размерам, указанным в таблице индивидуальных заданий (приложение 1). Образец выполнения – рис. 4.

Перед выполнением контрольного задания №2 рекомендуется ответить на вопросы 19 -32 из приложения 2 и решить задачи 22 – 34 из приложения 3.

Рис. 4

Контрольная задача №3

Построить три проекции тела, ограниченного поверхностью вращения, с вырезом (сквозным отверстием).

Указания к решению

Задача выполняется на листе чертежной бумаги формата А4 (210х297), в масшта­бе 1:1 по размерам, указанным в таблице индивидуальных заданий (приложение 1). Образец выполнения – рис. 5. Каждую линию сечения обвести своим цветом на трех плоскостях проекций, а очерки и проекции прямых пересечения плоскостей выреза - простым карандашом.

Перед выполнением рекомендуется ответить на вопросы 22- 26, 29 - 32 из приложения 2 и ре­шить задачи 32, 35, 37 из приложения 3.

Рис. 5

Контрольная задача № 4

Построить три проекции линии пересечения поверхностей вра­щения, одна из которых является проецирующим цилиндром.

Указания к решению

Задача выполняется на листе формата А3 (297х420) в масшта­бе 1:1 по размерам, указанным в таблице индивидуальных заданий (приложение 1). Образец выполнения - рис.6. Линию пересечения обвести цветным карандашом, а очерки сложной поверхности – простым. В правой

свободной части формата записать характерные точки линии пересечения.

Перед выполнением рекомендуется ответить на вопросы 33 - 40 из приложения 2 и решить задачи 38, 39 из приложения 3.

Рис. 6

Контрольная задача № 5

Построить три проекции линии пересечения поверхностей вращения.

Указания к решению

Задача выполняется на листе формата А3 (297х420) в масшта­бе 1:1 по размерам, указанным в таблице индивидуальных заданий (приложение 1).

Образец выполнения - рис. 7. Линию пересечения обвести цветным карандашом, а очерки сложной поверхности – простым. В правой

свободной части формата записать характерные точки линии пересечения.

Перед выполнением рекомендуется ответить на вопросы 33 - 40 из приложения 2 и решить задачи 38, 39 из приложения 3.

Рис. 7

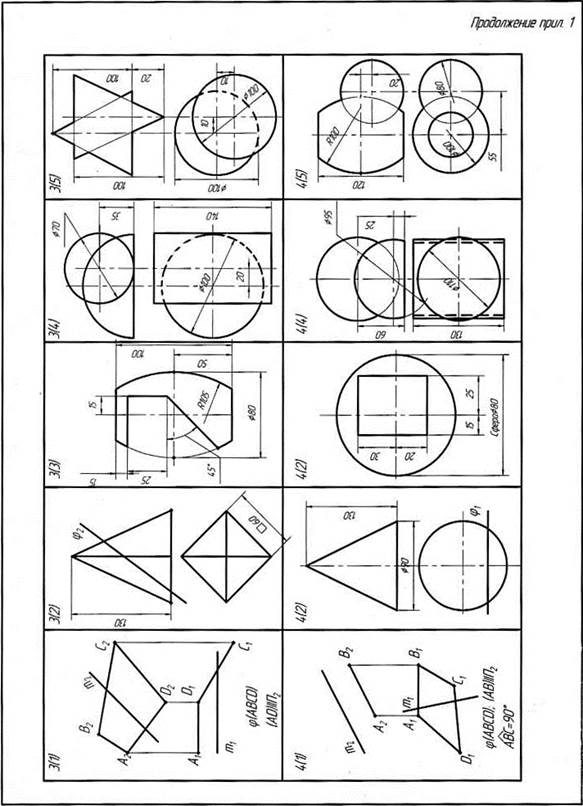
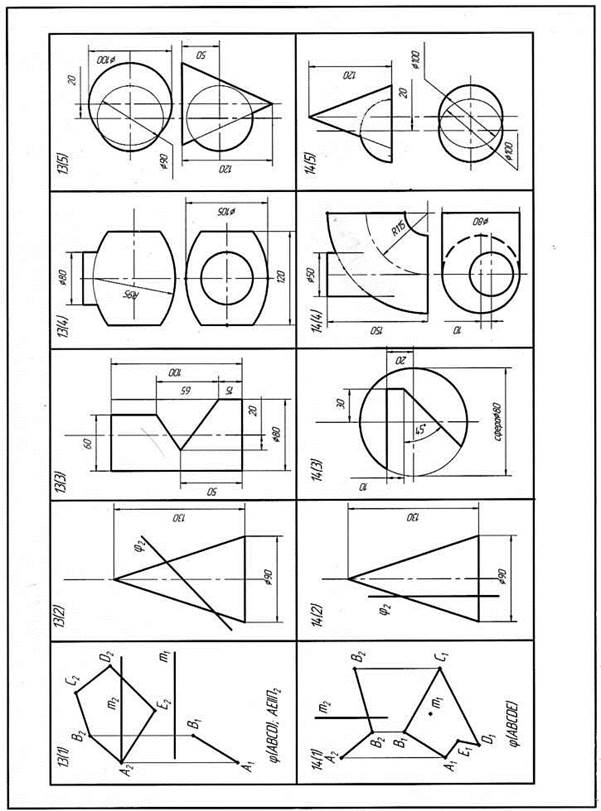
Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 2

ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ

Точка

1. Перечислите элементы аппарата центрального и параллельного проецирования. На наглядном чертеже изобразите проецирование точки на плоскость.

2. Назовите три закономерности построения комплексного чертежа (проекционная связь между горизонтальной, фронтальной и профильной проекциями точки). Какое количество проекций точки достаточно для определения ее положения в пространстве?

3. В чем различие между абсолютными и относительными координатами точки? Изобразите точку В, расположенную ближе, выше и левее точки А.

Прямая

4. Дайте определение прямых общего положения, уровня, проецирующих. Изобразите и обозначьте их на комплексном чертеже. Какими буквами латинского алфавита обозначаются прямые? Что такое вырожденная проекция прямой?

5. Какое количество изображений прямой на комплексном чертеже достаточно для определения ее положения в пространстве?

6. Изобразите и обозначьте на комплексном чертеже точку, принад­лежащую прямой.

7. Изобразите на комплексном чертеже и обозначьте параллельные, пересекающиеся и скрещивающиеся прямые.

8. Изобразите скрещивающиеся прямые. Обозначьте на их проекциях пары горизонтально- и фронтально-конкурирующих точек. С помощью какой пары конкурирующих точек определяется взаимное положение прямых по высоте? Какие конкурирующие точки определяют взаимное положение прямых по глубине (ближе, дальше)?

Плоскость

9. Какими геометрическими элементами можно задать плоскость на комплексном чертеже? Изобразите все возможные случаи задания плоскости. Какими буквами греческого алфавита обозначаются плоскости?

10. Какими геометрическими элементами можно задать плоскость общего положения?

11. Изобразите и обозначьте на чертеже плоскости уровня и проецирующие. Что такое вырожденная проекция плоскости?

12. Назовите количество изображений плоскости на комплексном чертеже, достаточное для определения ее положения в пространстве.

13. Перечислите возможные случаи взаимного положения прямой и плоскости.

14. Сформулируйте признаки принадлежности прямой и точки к плоскости. Изобразите на комплексном, чертеже какую-либо прямую и точку, принадлежащие плоскостям общего и частного положения.

15. Сформулируйте признак параллельности прямой и плоскости на комплексном чертеже и изобразите прямую, параллельную плоскости общего (и частного) положения.

16. Как определяется точка пересечения прямой с плоскостями общего положения и частного? Имеет ли значение для результата положение вспомогательной плоскости, в которую заключают прямую для нахождения точки пересечения прямой и плоскости общего положения?

17. Какие конкурирующие точки (фронтально-конкурирующие, горизонтально-конкурирующие) используются для определения видимости прямой, пересекающей плоскость, на П₁ и на П₂?

18. Используя признак параллельности плоскостей, изобразите на комплексном чертеже параллельные и пересекавшиеся пары плоскостей общего и частного положения.

Методы преобразования чертежа

19. Определите натуральную величину отрезка прямой общего положения методом вращения вокруг проецирующей прямой и методом замены плоскостей проекций. Отметьте полученное утлы наклона (a, b) прямой к плоскостям проекций (П₁, П₂).

20. Определите натуральную величину плоской фигуры, лежащей в проецирующей плоскости, вращением вокруг проецирующей прямой.

21. Как определяется направление новой оси Х^¢ при преобразовании методом замены плоскостей проекций плоскости общего положения в плоскость проецирующую; проецирующей плоскости в плоскость уровня?

Поверхности

22. В чем заключается кинематический способ образования поверхностей? Как образуются гранная поверхность и поверхность вращения.

23. Изобразите на комплексном чертеже гранную поверхность проекциями ее ребер. Определите видимость ребер с помощью конкурирующих точек. Задайте произвольно горизонтальную проекцию точки, лежащей на любой грани многогранника, и достройте ее недостающую проекцию.

24. Сформулируйте понятие меридиана поверхности вращения и ее параллели. Почему параллели любой поверхности вращения являются окружностями? Почему меридианом поверхности вращения всегда является ее образующая?

25. Что такое контур и очерк поверхности вращения? Задайте на комплексном чертеже прямой круговой цилиндр горизонтальным, фронтальным и профильным очерками. Обведите три проекции горизонтального, фронтального и профильного контуров цилиндра. То же самое проделайте для прямого кругового конуса и сферы.

26. Сформулируйте признак принадлежности точки к поверхности. Задайте на каждой из поверхностей (цилиндр, конус, сфера) произвольно фронтальную проекцию точки и найдите ее горизонтальную и профильную проекции.

27. Что представляет собой сечение многогранника плоскостью?

28. Как определяются вершины и стороны фигуры сечения? Изобразите две проекции треугольной пирамиды и проведите плоскость частного положения так, чтобы она рассекала пирамиду по четырехугольнику. Обведите проекции фигуры сечения с учетом ее видимости.

29. Сформулируйте понятие линии сечения поверхности вращения плоскостью. Чему равен порядок этой линии?

30. Перечислите кривые, получающиеся в сечении конуса плоскостью. При каком соотношении угла наклона образующей конуса к его оси и угла наклона секущей плоскости к этой же оси получаются в сечении окружность, парабола, эллипс, гипербола? В каком случае в сечении конуса получаются образующие?

31. Перечислите, какие линии получаются в сечении цилиндра плоскостью?

32. Какую кривую можно получить в сечении шара плоскостью? Какими линиями по форме могут быть ее проекции?

33. Сформулируйте понятие линии пересечения двух поверхностей. Чему равен порядок этой линии в общем случае пересечения?

34. Каким условиям должны удовлетворять вспомогательные секущие плоскости, используемые для построения линии пересечения двух поверхностей?

35. Какое положение относительно плоскостей проекций занимает плоскость общей симметрии двух пересекающихся поверхностей, если пересекаются: а) горизонтальные контуры этих поверхностей; б) их фронтальные контуры; в) их профильные контуры? Будут ли пересекаться фронтальные контуры поверхностей, если плоскость их общей симметрии является горизонтально-проецирующей?

36. Как определяются минимальный и максимальный радиусы вспомогательных сфер для построения линии пересечения двух поверхностей вращения методом концентрических сфер?

37. На контуре какой из двух пересекающихся поверхностей лежат точки – границы видимости линии их пересечения?

38. Назовите частные случая пересечения поверхностей.

39. По какой линии пересекаются соосные поверхности?

40. Какие линии возможно получить в пересечении по теореме Монжа:а) двух конусов; б) конуса и цилиндра в) двух цилиндров?

Приложение 3

Контрольная работа №1

По начертательной геометрии

Она включает 5 комплексных задач. Варианты графических заданий приведены в приложении 1. Всего 20 вариантов: каждая строчка – номер варианта – содержит 5 задач. Таким образом, нумерация задачи 1(4) соответствует первому варианту четвертой контрольной задачи.

Контрольная задача №1

Достроить недостающую проекцию плоскости общего положения j. Найти точку пересечения К прямой m с плоскостью j и определить видимость прямой. Записать координаты точки К отно­сительно точки А. Построить натуральную величину плоской фигуры АВК.

Указания к решению

Задание выполняется на листе чертежной бумаги формата АЗ (297х420). Образец выполнения – рис. 3.

Перед выполнением контрольного задания №1 рекомендуется ответить на вопросы 1 - 21 из приложения 2 и решить задачи 1 – 27 из приложения 3.

Рис. 3

Контрольная задача №2

Построить линию пересечения заданной поверхности проецирующей плоскостью. Определить характер линии сечения и натуральную величину плоской фигуры, полученной в сечении, построить развертку заданной поверхности и нанести на нее линию сечения.

Указания к решению

Задача выполняется на листе формата А3 (297х420).

В левой части формата вычерчивается графи­ческое условие задачи в масштабе 1:1 по размерам, указанным в таблице индивидуальных заданий (приложение 1). Образец выполнения – рис. 4.

Перед выполнением контрольного задания №2 рекомендуется ответить на вопросы 19 -32 из приложения 2 и решить задачи 22 – 34 из приложения 3.

Рис. 4

Контрольная задача №3

Построить три проекции тела, ограниченного поверхностью вращения, с вырезом (сквозным отверстием).

Указания к решению

Задача выполняется на листе чертежной бумаги формата А4 (210х297), в масшта­бе 1:1 по размерам, указанным в таблице индивидуальных заданий (приложение 1). Образец выполнения – рис. 5. Каждую линию сечения обвести своим цветом на трех плоскостях проекций, а очерки и проекции прямых пересечения плоскостей выреза - простым карандашом.

Перед выполнением рекомендуется ответить на вопросы 22- 26, 29 - 32 из приложения 2 и ре­шить задачи 32, 35, 37 из приложения 3.

Рис. 5

Контрольная задача № 4

Построить три проекции линии пересечения поверхностей вра­щения, одна из которых является проецирующим цилиндром.

Указания к решению

Задача выполняется на листе формата А3 (297х420) в масшта­бе 1:1 по размерам, указанным в таблице индивидуальных заданий (приложение 1). Образец выполнения - рис.6. Линию пересечения обвести цветным карандашом, а очерки сложной поверхности – простым. В правой

свободной части формата записать характерные точки линии пересечения.

Перед выполнением рекомендуется ответить на вопросы 33 - 40 из приложения 2 и решить задачи 38, 39 из приложения 3.

Рис. 6

Контрольная задача № 5

Построить три проекции линии пересечения поверхностей вращения.

Указания к решению

Задача выполняется на листе формата А3 (297х420) в масшта­бе 1:1 по размерам, указанным в таблице индивидуальных заданий (приложение 1).

Образец выполнения - рис. 7. Линию пересечения обвести цветным карандашом, а очерки сложной поверхности – простым. В правой

свободной части формата записать характерные точки линии пересечения.

Перед выполнением рекомендуется ответить на вопросы 33 - 40 из приложения 2 и решить задачи 38, 39 из приложения 3.

Рис. 7

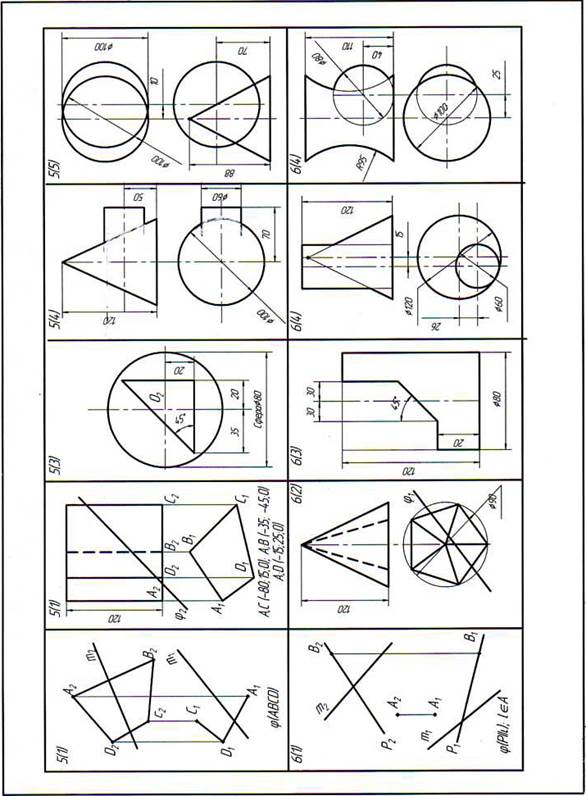
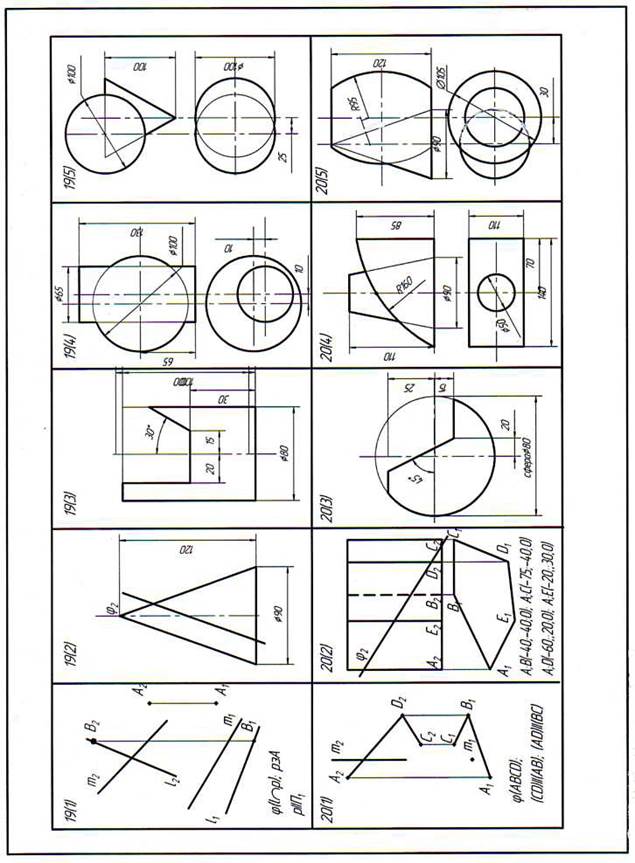
Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 1

Приложение 2

ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ

Точка

1. Перечислите элементы аппарата центрального и параллельного проецирования. На наглядном чертеже изобразите проецирование точки на плоскость.

2. Назовите три закономерности построения комплексного чертежа (проекционная связь между горизонтальной, фронтальной и профильной проекциями точки). Какое количество проекций точки достаточно для определения ее положения в пространстве?

3. В чем различие между абсолютными и относительными координатами точки? Изобразите точку В, расположенную ближе, выше и левее точки А.

Прямая

4. Дайте определение прямых общего положения, уровня, проецирующих. Изобразите и обозначьте их на комплексном чертеже. Какими буквами латинского алфавита обозначаются прямые? Что такое вырожденная проекция прямой?

5. Какое количество изображений прямой на комплексном чертеже достаточно для определения ее положения в пространстве?

6. Изобразите и обозначьте на комплексном чертеже точку, принад­лежащую прямой.

7. Изобразите на комплексном чертеже и обозначьте параллельные, пересекающиеся и скрещивающиеся прямые.

8. Изобразите скрещивающиеся прямые. Обозначьте на их проекциях пары горизонтально- и фронтально-конкурирующих точек. С помощью какой пары конкурирующих точек определяется взаимное положение прямых по высоте? Какие конкурирующие точки определяют взаимное положение прямых по глубине (ближе, дальше)?

Плоскость

9. Какими геометрическими элементами можно задать плоскость на комплексном чертеже? Изобразите все возможные случаи задания плоскости. Какими буквами греческого алфавита обозначаются плоскости?

10. Какими геометрическими элементами можно задать плоскость общего положения?

11. Изобразите и обозначьте на чертеже плоскости уровня и проецирующие. Что такое вырожденная проекция плоскости?

12. Назовите количество изображений плоскости на комплексном чертеже, достаточное для определения ее положения в пространстве.

13. Перечислите возможные случаи взаимного положения прямой и плоскости.

14. Сформулируйте признаки принадлежности прямой и точки к плоскости. Изобразите на комплексном, чертеже какую-либо прямую и точку, принадлежащие плоскостям общего и частного положения.

15. Сформулируйте признак параллельности прямой и плоскости на комплексном чертеже и изобразите прямую, параллельную плоскости общего (и частного) положения.

16. Как определяется точка пересечения прямой с плоскостями общего положения и частного? Имеет ли значение для результата положение вспомогательной плоскости, в которую заключают прямую для нахождения точки пересечения прямой и плоскости общего положения?

17. Какие конкурирующие точки (фронтально-конкурирующие, горизонтально-конкурирующие) используются для определения видимости прямой, пересекающей плоскость, на П₁ и на П₂?

18. Используя признак параллельности плоскостей, изобразите на комплексном чертеже параллельные и пересекавшиеся пары плоскостей общего и частного положения.

Методы преобразования чертежа

19. Определите натуральную величину отрезка прямой общего положения методом вращения вокруг проецирующей прямой и методом замены плоскостей проекций. Отметьте полученное утлы наклона (a, b) прямой к плоскостям проекций (П₁, П₂).

20. Определите натуральную величину плоской фигуры, лежащей в проецирующей плоскости, вращением вокруг проецирующей прямой.

21. Как определяется направление новой оси Х^¢ при преобразовании методом замены плоскостей проекций плоскости общего положения в плоскость проецирующую; проецирующей плоскости в плоскость уровня?

Поверхности

22. В чем заключается кинематический способ образования поверхностей? Как образуются гранная поверхность и поверхность вращения.

23. Изобразите на комплексном чертеже гранную поверхность проекциями ее ребер. Определите видимость ребер с помощью конкурирующих точек. Задайте произвольно горизонтальную проекцию точки, лежащей на любой грани многогранника, и достройте ее недостающую проекцию.

24. Сформулируйте понятие меридиана поверхности вращения и ее параллели. Почему параллели любой поверхности вращения являются окружностями? Почему меридианом поверхности вращения всегда является ее образующая?

25. Что такое контур и очерк поверхности вращения? Задайте на комплексном чертеже прямой круговой цилиндр горизонтальным, фронтальным и профильным очерками. Обведите три проекции горизонтального, фронтального и профильного контуров цилиндра. То же самое проделайте для прямого кругового конуса и сферы.

26. Сформулируйте признак принадлежности точки к поверхности. Задайте на каждой из поверхностей (цилиндр, конус, сфера) произвольно фронтальную проекцию точки и найдите ее горизонтальную и профильную проекции.

27. Что представляет собой сечение многогранника плоскостью?

28. Как определяются вершины и стороны фигуры сечения? Изобразите две проекции треугольной пирамиды и проведите плоскость частного положения так, чтобы она рассекала пирамиду по четырехугольнику. Обведите проекции фигуры сечения с учетом ее видимости.

29. Сформулируйте понятие линии сечения поверхности вращения плоскостью. Чему равен порядок этой линии?

30. Перечислите кривые, получающиеся в сечении конуса плоскостью. При каком соотношении угла наклона образующей конуса к его оси и угла наклона секущей плоскости к этой же оси получаются в сечении окружность, парабола, эллипс, гипербола? В каком случае в сечении конуса получаются образующие?

31. Перечислите, какие линии получаются в сечении цилиндра плоскостью?

32. Какую кривую можно получить в сечении шара плоскостью? Какими линиями по форме могут быть ее проекции?

33. Сформулируйте понятие линии пересечения двух поверхностей. Чему равен порядок этой линии в общем случае пересечения?

34. Каким условиям должны удовлетворять вспомогательные секущие плоскости, используемые для построения линии пересечения двух поверхностей?

35. Какое положение относительно плоскостей проекций занимает плоскость общей симметрии двух пересекающихся поверхностей, если пересекаются: а) горизонтальные контуры этих поверхностей; б) их фронтальные контуры; в) их профильные контуры? Будут ли пересекаться фронтальные контуры поверхностей, если плоскость их общей симметрии является горизонтально-проецирующей?

36. Как определяются минимальный и максимальный радиусы вспомогательных сфер для построения линии пересечения двух поверхностей вращения методом концентрических сфер?

37. На контуре какой из двух пересекающихся поверхностей лежат точки – границы видимости линии их пересечения?

38. Назовите частные случая пересечения поверхностей.

39. По какой линии пересекаются соосные поверхности?

40. Какие линии возможно получить в пересечении по теореме Монжа:а) двух конусов; б) конуса и цилиндра в) двух цилиндров?

Приложение 3

Комплексный чертеж точки. Абсолютные

Познавательные статьи:



Техника прыжка в длину с разбега

Организация работы процедурного кабинета

Области применения синхронных машин

Оптимизация по Винеру и Калману