
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие принадлежности двух прямых к одной плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Прямые лежат в одной плоскости. если они 1) пересекаются;2) параллельны. Для принадлежности прямых L1: Т.к. условие параллельности двух прямых имеет вид: Пример. Исследовать взаимное расположение прямых: L1: Направляющий вектор прямой L1– q1 =(1;3;-2). Прямая L2 задана как пересечение 2-х плоскостей α1: х-у-z+1=0; α2: x+y+2z-2=0. Т.к. прямая L2 лежит в обеих плоскостях, то она, а значит и ее направляющий вектор, перпендикулярна нормалям n1 и n2. Следовательно, направляющий вектор s2 является векторным произведением векторов n1 и n2, т.е. q2 = n1 х n2 = Т.о. s1 =- s2, значит прямые или параллельны, или совпадают. Чтобы проверить совпадают ли прямые, подставим координаты точки М0(1;2;-1) 1+2+4-2=0 следовательно прямые параллельны. Расстояние от точки до прямой. Расстояние от точки М1(х1;у1;z1) до прямой L, заданной каноническим уравнением L:
Построим параллелограмм на векторах q и М0М1. Тогда расстояние от точки М1 до прямой L равно высоте h этого параллелограмма. Т.к. S=| q x М0М1 |=h| q |, то h= Расстояние между двумя прямыми в пространстве. L1: 1) L1||L2. d= 2) L1 и L2 – скрещивающиеся d= Взаимное расположение прямой и плоскости в пространстве. Для расположения прямой и плоскости в пространстве возможны 3 случая: - прямая и плоскость пересекаются в одной точке; - прямая и плоскость параллельны; - прямая лежит в плоскости. Пусть прямая задана своим каноническим уравнением, а плоскость – общим L: α: Ах+Ву+Сz+D=0 Уравнения прямой дают точку М0(х0;у0;z0) Пересечение прямой и плоскости. Если прямая и плоскость пересекаются, то направляющий вектор прямой q не параллелен плоскости α, а значит не ортогонален нормальному вектору плоскости n. Т.е. их скалярное произведение n·q ≠0 или, через их координаты, Am+Bn+Cp≠0 (10)
Перейдем от канонического уравнения прямой к параметрическому: Подставим эти соотношения в уравнение плоскости А(x0+lt)+B(y0+mt)+C(z0+nt)+D=0 A,B,C,D,l,m,n,x0,y0,z0 – известны, найдем параметр t: t(Al+Bm+Cn)= -D-Ax0-By0-Cz0 если Am+Bn+Cp≠0, то уравнение имеет единственное решение, определяющее координаты точки М: tМ= - Угол между прямой и плоскостью. Условия параллельности и перпендикулярности.
с направляющим вектором q ={l;m;n} и плоскостью p: Ах+Ву+Сz+D=0 с нормальным вектором n =(A;B;C) находится в пределах от 0˚ (в случае параллельности прямой и плоскости) до 90˚ (в случае перпендикулярности прямой и плоскости). (Угол между вектором q и его проекцией на плоскость α). y– угол между векторами q и n. Т.к. угол j между прямой L и плоскостью p является дополнительным к углу y, то sin φ=sin( sin φ= Условие параллельности прямой и плоскости. L||p Условие перпендикулярности прямой и плоскости. L Условие принадлежности прямой L к плоскости α. Для того, чтобы прямая L: 1) L||p; 2) Одна из точек прямой L, например точка М0(х0,у0,z0), принадлежит плоскости p. Т.о. условие принадлежности прямой плоскости:
Пример. Составить уравнение плоскости, проходящей через точку М(4;-3;6) перпендикулярно прямой Из условия следует, что в качестве нормального вектора плоскости можно взять направляющий вектор прямой, т.е. n =q=(1;1;-2), получаем уравнение: x+y-2z+D=0. Подставляя в это уравнение координаты точки М, Найдем значение параметра D. Связка прямых. Совокупность всех прямых, проходящих через точку М1(x1,y1,z1), называется связкой прямых (с центром в точке М1). Уравнения связки прямых с центром в точке М1 имеют вид:
где l, m, n - произвольные числа, такие, что l2+m2+n2¹0/ Действительно, всякая прямая, определяемая уравнениями (16), проходит через точку М1(x1,y1,z1). С другой стороны, если L – наперед заданная прямая, проходящая через точку М1(x1,y1,z1), то эта прямая однозначно определяется заданием, кроме точки М1(x1,y1,z1), направляющим вектором q ={l;m;n} и потому определяются каноническими уравнениями, совпадающими с уравнениями (16).
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 997; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 и L2:
и L2:  одной плоскости Û чтобы векторы М1М2 ={x2-x1;y2-y1;z2-z1}, q1 ={l1;m1;n1} и q2 ={l2;m2;n2} были компланарны. Т.е., по условию компланарности трех векторов, смешанное произведение М1М2·s1·s2 =Δ=
одной плоскости Û чтобы векторы М1М2 ={x2-x1;y2-y1;z2-z1}, q1 ={l1;m1;n1} и q2 ={l2;m2;n2} были компланарны. Т.е., по условию компланарности трех векторов, смешанное произведение М1М2·s1·s2 =Δ=  =0 (8)
=0 (8) , то для пересечения прямых L1 и L2 Û, чтобы они удовлетворяли условию (8) и чтобы нарушалась хотя бы одна из пропорций
, то для пересечения прямых L1 и L2 Û, чтобы они удовлетворяли условию (8) и чтобы нарушалась хотя бы одна из пропорций  , L2:
, L2: 
 =- i -3 j +2 k.
=- i -3 j +2 k. L1 в общие уравнения L2: 1-2+2+1=0 – неверные равенства, т.е. точка М0
L1 в общие уравнения L2: 1-2+2+1=0 – неверные равенства, т.е. точка М0  L2,
L2,  можно вычислить при помощи векторного произведения.
можно вычислить при помощи векторного произведения. Из канонического уравнения прямой следует, что точка М0(х0;у0;z0)
Из канонического уравнения прямой следует, что точка М0(х0;у0;z0)  (9)
(9)

 Определим координаты точки М - точки пересечения прямой L и плоскости α.
Определим координаты точки М - точки пересечения прямой L и плоскости α. , t
, t  →
→  (11)
(11) Угол φ между прямой L:
Угол φ между прямой L:  -y)=cos y=
-y)=cos y=  - (рассматривается абсолютная величина т.к. угол φ острый sin φ=sin(
- (рассматривается абсолютная величина т.к. угол φ острый sin φ=sin( (12)
(12) n
n 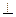 q
q  p
p  (14)
(14) (15)
(15) .
. (16)
(16)


