Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
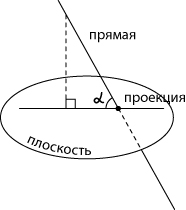
Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной. Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.
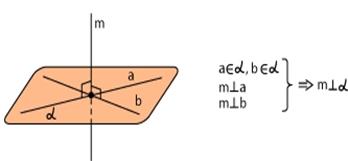
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость. Обратите внимание – в качестве угла между прямой и плоскостью мы выбираем острый угол. Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю. Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°. Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Это определение. Но как же с ним работать? Как проверить, что данная прямая перпендикулярна всем прямым, лежащим в плоскости? Ведь их там бесконечно много. На практике применяется признак перпендикулярности прямой и плоскости: Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Тема 7.3. Многогранники Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Сечения многогранников. Построение сечений. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Многогранник – геометрическое тело, ограниченное со всех сторон плоскими многоугольниками – гранями. Стороны граней называются ребрами, а концы ребер – вершинами. По числу граней различают 4-гранники, 5-гранники и т.д. Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой его грани. Многогранник называется правильным, если его грани правильные многоугольники (т.е. такие, у которых все стороны и углы равны) и все многогранные углы при вершинах равны. Существует пять видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Многогранник в трехмерном пространстве (понятие многогранника) – совокупность конечного числа плоских многоугольников такая, что 1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне); 2) от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя к смежному с ним, а от этого в свою очередь – к смежному с ним, и т.д. Эти многоугольники называются гранями, их стороны ребрами, а их вершины – вершинами многогранника. Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани. Из этого определения следует, что все грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней. Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы. Разверткой многогранника – многогранной поверхности – называется совокупность многоугольников, для которой указано, как их нужно склеивать – прикладывать друг к другу по сторонам. Конечно, склеиваемые стороны должны быть равны, и нужно указывать, какой конец одной стороны должен совпадать с каким концом другой стороны. При составлении – склеивании многогранной поверхности – многоугольники развертки могут «переламываться». Многогранные углы можно получить, продолжая ребра и грани, идущие из одной вершины какого-либо многогранника, например, из вершины пирамиды. Многогранные углы составляются из обычных углов (такие углы мы теперь часто будем называть плоскими углами), подобно тому, как замкнутая ломаная составляется из отрезков. А именно, дается следующее определение: Многогранным углом называется фигура, образованная плоскими углами так, что выполнены условия: 1) никакие два угла не имеют общих точек, кроме их общей вершины или целой стороны; 2) у каждого из этих углов каждая его сторона является общей с одним и только одним другим таким углом; 3) от каждого угла к каждому можно перейти по углам, имеющим общие стороны; 4) никакие два угла с общей стороной не лежат в одной плоскости.
При этих условиях плоские углы, образующие многогранный угол, называются его гранями, а их стороны – его ребрами. Теорема Эйлера. Пусть В – число вершин выпуклого многогранника, Р – число его ребер и Г – число граней. Тогда верно равенство В–Р+Г=2. Число В–Р+Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2. То, что эйлерова характеристика равна 2 для некоторых знакомых нам многогранников, видно из таблицы. Многогранник В Р Г Тетраэдр 4 6 4 2 Октаэдр 6 12 8 2 Параллелепипед 8 12 6 2 n-угольная пирамида n+1 2n n+1 2 n-угольная призма 2n 3n n+2 2 Некоторые пространственные фигуры Хотя изучение пространственных фигур нам еще предстоит, мы будем использовать отдельные виды многогранников при рассмотрении ряда вопросов стереометрии. Напомним некоторые сведения о многогранниках и дадим каждому многограннику наглядное описание. Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников (рис. 1–10). Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми (рис. 1) и невыпуклыми (рис. 2). Выпуклый многогранник расположен по одну сторону относительно плоскости, проходящей через любую его грань. (Мы будем изучать только выпуклые многогранники.) Приведем примеры отдельных многогранников. Куб представляет собой многогранник, у которого Параллелепипед представляет собой многогранник, у которого шесть граней, и каждая из них – параллелограмм. Параллелепипед может быть прямым (рис. 4) или наклонным (рис. 5). Параллелепипед, все грани которого прямоугольники, называют прямоугольным. Прямоугольный параллелепипед изображается так же, как и прямой. Из сказанного следует, что куб – это прямоугольный параллелепипед с равными ребрами.
Параллелепипед – это призма, в основании которой лежит параллелограмм.
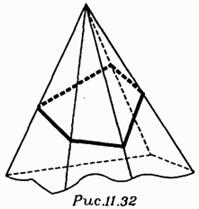
Сечение параллелограмма 1. Сечение параллелепипеда плоскостью, параллельной грани. В сечении образуется параллелограмм. 2. Сечение параллелепипеда плоскостью, проходящей через противолежащие ребра. В сечении образуется параллелограмм. В некоторых случаях в сечении может образоваться ромб, прямоугольник или квадрат. Сечение призмы 1. Сечение призмы плоскостью, параллельной основанию. В сечении образуется многоугольник, равный многоугольнику, лежащему в основании. 2. Сечение призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение называется диагональным сечением призмы. В некоторых случаях может получаться ромб, прямоугольник или квадрат. Сечение правильной призмы 1. Сечение правильной призмы плоскостью, параллельной основанию. В сечении образуется правильный многоугольник, равный многоугольнику, лежащему в основании. 2. Сечение правильной призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется прямоугольник. В некоторых случаях может образоваться квадрат. Сечение правильной пирамиды 1. Сечение правильной пирамиды плоскостью, параллельной основанию. В сечении образуется правильный многоугольник, подобный многоугольнику, лежащему в основании. 2. Сечение правильной пирамиды плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется равнобедренный треугольник. В некоторых случаях может образоваться равносторонний треугольник. Понятие о симметрии в пространстве. Слово симметрия происходит от греческого symmetria, которое означает «соразмерность». Греческий скульптор Поликлет, очевидно, был первым, кто использовал термин симметрия еще в V в. до н. э. Во времена Пифагора (V в. до н. э.) и пифагорейцев понятие симметрии было оформлено достаточно четко. В то же время они могли подвергнуть его серьезному анализу и получить результаты универсального назначения. Можно выделить важный момент в их учении. Диалектичность и современность: «мир – множество, и состоит из противоположностей», «то, что приводит противоположности к единству, и создает все в космосе», есть симметрия; симметрия и заключается в числовых отношениях (математических). Но математически строгое представление о симметрии сформировалось сравнительно недавно – в XIX в. В наиболее простой трактовке известного немецкого математика Г. Вейля (1855 – 1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как – то изменять, получая в результате то же, с чего начали (см. рис. 1).
Современное представление симметрии предполагает неизменность объекта по отношению к каким – то преобразованиям, выполняемым над ними. Например, пятиконечная звезда, будучи повернута на 72° (360°: 5), займет свое первоначальное положение. Раскрыв понятие симметрии, необходимо рассмотреть ее виды. Выделяют несколько классификаций, но рассмотрим следующие: Ø В случае центральной симметрии (инверсии) относительно точки О фигура Ф совмещается сама с собой после последовательных отражений от трёх взаимно перпендикулярных плоскостей, другими словами, точка О — середина отрезка, соединяющего симметричные точки Ф (см. рис. 2).
В случае осевой симметрии, или симметрии относительно прямой n-го порядка, фигура накладывается на себя вращением вокруг некоторой прямой (оси симметрии) на угол 360°/n. Например, куб имеет прямую AB осью симметрии третьего порядка, а прямую CD Слово симметрия происходит от греческого symmetria, которое означает «соразмерность». Греческий скульптор Поликлет, очевидно, был первым, кто использовал термин симметрия еще в V в. до н. э. Во времена Пифагора (V в. до н. э.) и пифагорейцев понятие симметрии было оформлено достаточно четко. В то же время они могли подвергнуть его серьезному анализу и получить результаты универсального назначения. Можно выделить важный момент в их учении. Диалектичность и современность: «мир – множество, и состоит из противоположностей», «то, что приводит противоположности к единству, и создает все в космосе», есть симметрия; симметрия и заключается в числовых отношениях (математических). Но математически строгое представление о симметрии сформировалось сравнительно недавно – в XIX в. В наиболее простой трактовке известного немецкого математика Г. Вейля (1855 – 1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как – то изменять, получая в результате то же, с чего начали (см. рис. 1).
Современное представление симметрии предполагает неизменность объекта по отношению к каким – то преобразованиям, выполняемым над ними. Например, пятиконечная звезда, будучи повернута на 72° (360°: 5), займет свое первоначальное положение. Раскрыв понятие симметрии, необходимо рассмотреть ее виды. Выделяют несколько классификаций, но рассмотрим следующие: В случае центральной симметрии (инверсии) относительно точки О фигура Ф совмещается сама с собой после последовательных отражений от трёх взаимно перпендикулярных плоскостей, другими словами, точка О Слово симметрия происходит от греческого symmetria, которое означает «соразмерность». Греческий скульптор Поликлет, очевидно, был первым, кто использовал термин симметрия еще в V в. до н. э. Во времена Пифагора (V в. до н. э.) и пифагорейцев понятие симметрии было оформлено достаточно четко. В то же время они могли подвергнуть его серьезному анализу и получить результаты универсального назначения. Можно выделить важный момент в их учении. Диалектичность и современность: «мир – множество, и состоит из противоположностей», «то, что приводит противоположности к единству, и создает все в космосе», есть симметрия; симметрия и заключается в числовых отношениях (математических). Но математически строгое представление о симметрии сформировалось сравнительно недавно – в XIX в. В наиболее простой трактовке известного немецкого математика Г. Вейля (1855 – 1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как – то изменять, получая в результате то же, с чего начали (см. рис. 1).
Современное представление симметрии предполагает неизменность объекта по отношению к каким – то преобразованиям, выполняемым над ними. Например, пятиконечная звезда, будучи повернута на 72° (360°: 5), займет свое первоначальное положение. Раскрыв понятие симметрии, необходимо рассмотреть ее виды. Выделяют несколько классификаций, но рассмотрим следующие: Ø В случае центральной симметрии (инверсии) относительно точки О фигура Ф совмещается сама с собой после последовательных отражений от трёх взаимно перпендикулярных плоскостей, другими словами, точка О — середина отрезка, соединяющего симметричные точки Ф (см. рис. 2).
Ø В случае осевой симметрии, или симметрии относительно прямой n-го порядка, фигура накладывается на себя вращением вокруг некоторой прямой (оси симметрии) на угол 360°/n. Например, куб имеет прямую AB осью симметрии третьего порядка, а прямую CD — осью симметрии четвёртого порядка (см. рис. 2); вообще, правильные и полуправильные многогранники симметричны относительно ряда прямых. Фигура, накладывающаяся на себя последовательным вращением на угол 360°/2k вокруг прямой AB и отражением в плоскости, перпендикулярной к ней, имеет зеркально-осевую симметрию. Прямая AB, называется зеркально-поворотной осью симметрии порядка 2k, является осью симметрии порядка k (см. рис. 3). Зеркально-осевая симметрии порядка 2 равносильна центральной симметрии.
Ø В случае симметрии переноса фигура накладывается на себя переносом вдоль некоторой прямой (оси переноса) на какой-либо отрезок. Например, фигура с единственной осью переноса обладает бесконечным множеством плоскостей симметрии (поскольку любой перенос можно осуществить двумя последовательными отражениями от плоскостей, перпендикулярных оси переноса) (см. рис. 4). Фигуры, имеющие несколько осей переноса, играют важную роль при исследовании кристаллических решёток.
Р
Ø Симметрия подобия представляет собой своеобразные аналог предыдущих симметрий с той лишь разницей, что связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки (см. рис. 5).
Ø Рис. 6. Стебель растения.
Ø Поворотная симметрия, которая проявляется в простейшей форме в том случае, когда поверхностью полной цилиндрической симметрии является плоскость, перпендикулярная оси. Прекрасные примеры такой поворотной плоской симметрии дают окна готических соборов в форме роз с красочными витражами (см. рис. 7). Рис. 7. Окна готического собора.
Существует много других видов симметрий, имеющих абстрактный характер. Например, Ø Перестановочная симметрия, которая состоит в том, что если тождественные частицы поменять местами, то никаких изменений не происходит. Ø Калибровочные симметрии связаны с изменением масштаба. Иногда фигуры могут обладать разными типами симметрии. Ø середина отрезка, соединяющего симметричные точки Ф (см. рис. 2).
В случае осевой симметрии, или симметрии относительно прямой n-го порядка, фигура накладывается на себя вращением вокруг некоторой прямой (оси симметрии) на угол 360°/n. Например, куб имеет прямую AB осью симметрии третьего порядка, а прямую CD Слово симметрия происходит от греческого symmetria, которое означает «соразмерность». Греческий скульптор Поликлет, очевидно, был первым, кто использовал термин симметрия еще в V в. до н. э. Во времена Пифагора (V в. до н. э.) и пифагорейцев понятие симметрии было оформлено достаточно четко. В то же время они могли подвергнуть его серьезному анализу и получить результаты универсального назначения. Можно выделить важный момент в их учении. Диалектичность и современность: «мир – множество, и состоит из противоположностей», «то, что приводит противоположности к единству, и создает все в космосе», есть симметрия; симметрия и заключается в числовых отношениях (математических). Но математически строгое представление о симметрии сформировалось сравнительно недавно – в XIX в. В наиболее простой трактовке известного немецкого математика Г. Вейля (1855 – 1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как – то изменять, получая в результате то же, с чего начали (см. рис. 1).
Современное представление симметрии предполагает неизменность объекта по отношению к каким – то преобразованиям, выполняемым над ними. Например, пятиконечная звезда, будучи повернута на 72° (360°: 5), займет свое первоначальное положение. Раскрыв понятие симметрии, необходимо рассмотреть ее виды. Выделяют несколько классификаций, но рассмотрим следующие: Ø В случае центральной симметрии (инверсии) относительно точки О фигура Ф совмещается сама с собой после последовательных отражений от трёх взаимно перпендикулярных плоскостей, другими словами, точка О — середина отрезка, соединяющего симметричные точки Ф (см. рис. 2).
Ø В случае осевой симметрии, или симметрии относительно прямой n-го порядка, фигура накладывается на себя вращением вокруг некоторой прямой (оси симметрии) на угол 360°/n. Например, куб имеет прямую AB осью симметрии третьего порядка, а прямую CD — осью симметрии четвёртого порядка (см. рис. 2); вообще, правильные и полуправильные многогранники симметричны относительно ряда прямых. Фигура, накладывающаяся на себя последовательным вращением на угол 360°/2k вокруг прямой AB и отражением в плоскости, перпендикулярной к ней, имеет зеркально-осевую симметрию. Прямая AB, называется зеркально-поворотной осью симметрии порядка 2k, является осью симметрии порядка k (см. рис. 3). Зеркально-осевая симметрии порядка 2 равносильна центральной симметрии.
Ø В случае симметрии переноса фигура накладывается на себя переносом вдоль некоторой прямой (оси переноса) на какой-либо отрезок. Например, фигура с единственной осью переноса обладает бесконечным множеством плоскостей симметрии (поскольку любой перенос можно осуществить двумя последовательными отражениями от плоскостей, перпендикулярных оси переноса) (см. рис. 4). Фигуры, имеющие несколько осей переноса, играют важную роль при исследовании кристаллических решёток.
Р
Ø Симметрия подобия представляет собой своеобразные аналог предыдущих симметрий с той лишь разницей, что связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки (см. рис. 5).
Ø Винтовая (спиральная) симметрия есть симметрия относительно комбинации двух преобразований - поворота и переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта (см. рис. 6). Рис. 6. Стебель растения.
Ø Поворотная симметрия, которая проявляется в простейшей форме в том случае, когда поверхностью полной цилиндрической симметрии является плоскость, перпендикулярная оси. Прекрасные примеры такой поворотной плоской симметрии дают окна готических соборов в форме роз с красочными витражами (см. рис. 7). Рис. 7. Окна готического собора.
Существует много других видов симметрий, имеющих абстрактный характер. Например, Ø Перестановочная симметрия, которая состоит в том, что если тождественные частицы поменять местами, то никаких изменений не происходит. Ø Калибровочные симметрии связаны с изменением масштаба. Иногда фигуры могут обладать разными типами симметрии. Например, поворотной и зеркальной симметрией обладают некоторые буквы: Ж, Н, Ф, О, Х. Ø осью симметрии четвёртого порядка (см. рис. 2); вообще, правильные и полуправильные многогранники симметричны относительно ряда прямых. Фигура, накладывающаяся на себя последовательным вращением на угол 360°/2k вокруг прямой AB и отражением в плоскости, перпендикулярной к ней, имеет зеркально-осевую симметрию. Прямая AB, называется зеркально-поворотной осью симметрии порядка 2k, является осью симметрии порядка k (см. рис. 3). Зеркально-осевая симметрии порядка 2 равносильна центральной симметрии.
Ø В случае симметрии переноса фигура накладывается на себя переносом вдоль некоторой прямой (оси переноса) на какой-либо отрезок. Например, фигура с единственной осью переноса обладает бесконечным множеством плоскостей симметрии (поскольку любой перенос можно осуществить двумя последовательными отражениями от плоскостей, перпендикулярных оси переноса) (см. рис. 4). Фигуры, имеющие несколько осей переноса, играют важную роль при исследовании кристаллических решёток.
Р
Ø Симметрия подобия представляет собой своеобразные аналог предыдущих симметрий с той лишь разницей, что связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки (см. рис. 5).
Винтовая (спиральная) симметрия есть симметрия относительно комбинации двух преобразований Слово симметрия происходит от греческого symmetria, которое означает «соразмерность». Греческий скульптор Поликлет, очевидно, был первым, кто использовал термин симметрия еще в V в. до н. э. Во времена Пифагора (V в. до н. э.) и пифагорейцев понятие симметрии было оформлено достаточно четко. В то же время они могли подвергнуть его серьезному анализу и получить результаты универсального назначения. Можно выделить важный момент в их учении. Диалектичность и современность: «мир – множество, и состоит из противоположностей», «то, что приводит противоположности к единству, и создает все в космосе», есть симметрия; симметрия и заключается в числовых отношениях (математических). Но математически строгое представление о симметрии сформировалось сравнительно недавно – в XIX в. В наиболее простой трактовке известного немецкого математика Г. Вейля (1855 – 1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как – то изменять, получая в результате то же, с чего начали (см. рис. 1).
Современное представление симметрии предполагает неизменность объекта по отношению к каким – то преобразованиям, выполняемым над ними. Например, пятиконечная звезда, будучи повернута на 72° (360°: 5), займет свое первоначальное положение. Раскрыв понятие симметрии, необходимо рассмотреть ее виды. Выделяют несколько классификаций, но рассмотрим следующие: Ø В случае центральной симметрии (инверсии) относительно точки О фигура Ф совмещается сама с собой после последовательных отражений от трёх взаимно перпендикулярных плоскостей, другими словами, точка О — середина отрезка, соединяющего симметричные точки Ф (см. рис. 2).
Ø В случае осевой симметрии, или симметрии относительно прямой n-го порядка, фигура накладывается на себя вращением вокруг некоторой прямой (оси симметрии) на угол 360°/n. Например, куб имеет прямую AB осью симметрии третьего порядка, а прямую CD — осью симметрии четвёртого порядка (см. рис. 2); вообще, правильные и полуправильные многогранники симметричны относительно ряда прямых. Фигура, накладывающаяся на себя последовательным вращением на угол 360°/2k вокруг прямой AB и отражением в плоскости, перпендикулярной к ней, имеет зеркально-осевую симметрию. Прямая AB, называется зеркально-поворотной осью симметрии порядка 2k, является осью симметрии порядка k (см. рис. 3). Зеркально-осевая симметрии порядка 2 равносильна центральной симметрии.
Ø В случае симметрии переноса фигура накладывается на себя переносом вдоль некоторой прямой (оси переноса) на какой-либо отрезок. Например, фигура с единственной осью переноса обладает бесконечным множеством плоскостей симметрии (поскольку любой перенос можно осуществить двумя последовательными отражениями от плоскостей, перпендикулярных оси переноса) (см. рис. 4). Фигуры, имеющие несколько осей переноса, играют важную роль при исследовании кристаллических решёток.
Р
Ø Симметрия подобия представляет собой своеобразные аналог предыдущих симметрий с той лишь разницей, что связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки (см. рис. 5).
Ø Винтовая (спиральная) симметрия есть симметрия относительно комбинации двух преобразований - поворота и переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта (см. рис. 6). Рис. 6. Стебель растения.
Ø Поворотная симметрия, которая проявляется в простейшей форме в том случае, когда поверхностью полной цилиндрической симметрии является плоскость, перпендикулярная оси. Прекрасные примеры такой поворотной плоской симметрии дают окна готических соборов в форме роз с красочными витражами (см. рис. 7). Рис. 7. Окна готического собора.
Существует много других видов симметрий, имеющих абстрактный характер. Например, Ø Перестановочная симметрия, которая состоит в том, что если тождественные частицы поменять местами, то никаких изменений не происходит. Ø Калибровочные симметрии связаны с изменением масштаба. Иногда фигуры могут обладать разными типами симметрии. Ø поворота и переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта (см. рис. 6). Рис. 6. Стебель растения.
Ø Поворотная симметрия, которая проявляется в простейшей форме в том случае, когда поверхностью полной цилиндрической симметрии является плоскость, перпендикулярная оси. Прекрасные примеры такой поворотной плоской симметрии дают окна готических соборов в форме роз с красочными витражами (см. рис. 7). Рис. 7. Окна готического собора.
Существует много других видов симметрий, имеющих абстрактный характер. Например, Ø Перестановочная симметрия, которая состоит в том, что если тождественные частицы поменять местами, то никаких изменений не происходит. Ø Калибровочные симметрии связаны с изменением масштаба. Иногда фигуры могут обладать разными типами симметрии. Ø осью симметрии четвёртого порядка (см. рис. 2); вообще, правильные и полуправильные многогранники симметричны относительно ряда прямых. Фигура, накладывающаяся на себя последовательным вращением на угол 360°/2k вокруг прямой AB и отражением в плоскости, перпендикулярной к ней, имеет зеркально-осевую симметрию. Прямая AB, называется зеркально-поворотной осью симметрии порядка 2k, является осью симметрии порядка k (см. рис. 3). Зеркально-осевая симметрии порядка 2 равносильна центральной симметрии.
Ø В случае симметрии переноса фигура накладывается на себя переносом вдоль некоторой прямой (оси переноса) на какой-либо отрезок. Например, фигура с единственной осью переноса обладает бесконечным множеством плоскостей симметрии (поскольку любой перенос можно осуществить двумя последовательными отражениями от плоскостей, перпендикулярных оси переноса) (см. рис. 4). Фигуры, имеющие несколько осей переноса, играют важную роль при исследовании кристаллических решёток.
Р
Ø Симметрия подобия представляет собой своеобразные аналог предыдущих симметрий с той лишь разницей, что связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки (см. рис. 5).
Ø Винтовая (спиральная) симметрия есть симметрия относительно комбинации двух преобразований - поворота и переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта (см. рис. 6). Рис. 6. Стебель растения.
Ø Поворотная симметрия, которая проявляется в простейшей форме в том случае, когда поверхностью полной цилиндрической симметрии является плоскость, перпендикулярная оси. Прекрасные примеры такой поворотной плоской симметрии дают окна готических соборов в форме роз с красочными витражами (см. рис. 7). Рис. 7. Окна готического собора.
Существует много других видов симметрий, имеющих абстрактный характер. Например, Ø Перестановочная симметрия, которая состоит в том, что если тождественные частицы поменять местами, то никаких изменений не происходит. Ø Калибровочные симметрии связаны с изменением масштаба. Иногда фигуры могут обладать разными типами симметрии. Например, поворотной и зеркальной симметрией обладают некоторые буквы: Ж, Н, Ф, О, Х. Симметрия куба 1. Центр симметрии – центр куба (точка пересечения диагоналей куба). 2. Плоскости симметрии: три плоскости симметрии, проходящие через середины параллельных ребер; шесть плоскостей симметрии, проходящие через противолежащие ребра.
3. Оси симметрии: три оси симметрии, проходящие через
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 906; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.48.237 (0.016 с.) |

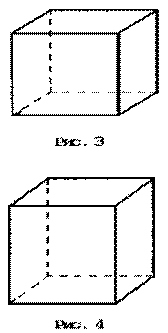 шесть граней, и все они – равные квадраты. У куба 12 равных ребер и 8 вершин (рис. 3).
шесть граней, и все они – равные квадраты. У куба 12 равных ребер и 8 вершин (рис. 3). -угольная пирамида представляет собой многогранник, одна грань которого, называемая основанием пирамиды, – некоторый выпуклый n-угольник, а остальные
-угольная пирамида представляет собой многогранник, одна грань которого, называемая основанием пирамиды, – некоторый выпуклый n-угольник, а остальные 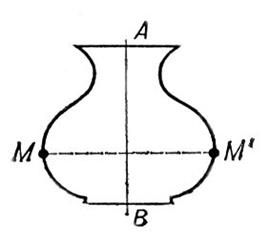 Рис. 1. Плоская симметричная фигура.
Рис. 1. Плоская симметричная фигура.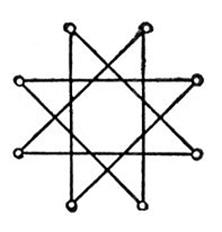 Рис. 2. Симметрия восьмого порядка. Правильный многоугольник.
Рис. 2. Симметрия восьмого порядка. Правильный многоугольник.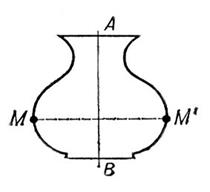 Рис. 1. Плоская симметричная фигура.
Рис. 1. Плоская симметричная фигура.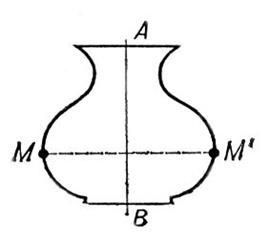 Рис. 1. Плоская симметричная фигура.
Рис. 1. Плоская симметричная фигура.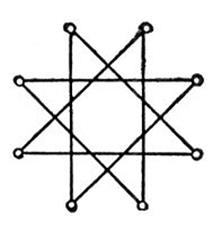 Рис. 2. Симметрия восьмого порядка. Правильный многоугольник.
Рис. 2. Симметрия восьмого порядка. Правильный многоугольник. Рис. 3. Симметрия. Бордюр.
Рис. 3. Симметрия. Бордюр. Рис. 4. Симметрия. Орнамент.
Рис. 4. Симметрия. Орнамент. Рис. 5. Матрешки.
Рис. 5. Матрешки.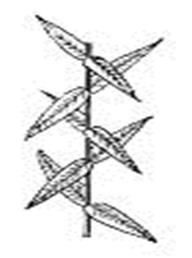 Винтовая (спиральная) симметрия есть симметрия относительно комбинации двух преобразований - поворота и переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта (см. рис. 6).
Винтовая (спиральная) симметрия есть симметрия относительно комбинации двух преобразований - поворота и переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта (см. рис. 6).
 Рис. 4. Симметрия. Орнамент.
Рис. 4. Симметрия. Орнамент.
 Рис. 4. Симметрия. Орнамент.
Рис. 4. Симметрия. Орнамент.