
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. 1. Функция и ее основные свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Выпуклость функции. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Сложная функция (композиция функций). Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной.
Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной Обозначение: Переменную Все значения, которые принимает Обозначения:
Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. Если некоторому значению
Способы задания функции 1) Функция может быть задана аналитически в виде формулы. Например, 2) Функция может быть задана таблицей из множества пар 3) Функция может быть задана графически. Пары значений
Определение: Функция
Определение. Функция График произвольной четной функции приведен на рисунке ниже.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.226 (0.009 с.) |

 от переменной
от переменной  называется функцией, если каждому значению
называется функцией, если каждому значению  .
. – область определения функции;
– область определения функции; – область значений функции;
– область значений функции; – значение функции в точке
– значение функции в точке  .
. соответствуют несколько значений (а не одно)
соответствуют несколько значений (а не одно)  , пересекалась с графиком не более чем в одной точке.
, пересекалась с графиком не более чем в одной точке.


 .
. называется четной, если для любого
называется четной, если для любого 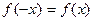 . График произвольной четной функции приведен на рисунке ниже.
. График произвольной четной функции приведен на рисунке ниже.
 .
.



