
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные законы комбинаторики.Содержание книги
Поиск на нашем сайте
Правило суммы. Пример. На блюде лежат 5 яблок и 2 груши. Сколькими способами можно выбрать один плод? Решение. Плод можно выбрать семью способами (5+2=7). Если некоторый элемент a может быть выбран из множества элементов На языке теории множеств это правило формулируется следующим образом: Теорема. Если пересечение конечных множеств пусто, то число элементов в их объединении равно сумме чисел элементов множеств А и В. Правило произведения. Вторым основным правилом комбинаторики является правило произведения. Пример. Определить количество клеток в игре «морской бой», если номер клетки состоит из буквы (букв 10) и цифры (цифр тоже 10). Решение. Количество клеток равно 10•10=100. Если элемент a можно выбрать из множества элементов На языке множеств это правило выражается в виде следующей теоремы. Теорема. Если множества Следствие. Если множества
Пример. Сколько номеров, состоящих из двух букв, за которыми идут три цифры можно составить, если использовать 29 букв и 10 цифр. Решение. Обозначим множество букв Правило суммы Правило суммы. Если некоторый объект А можно выбрать Пример. От Октябрьской площади до цирка можно проехать через Северную и Южную дамбы. В первом случае количество дорог равно 4, а во втором – 3. Сколькими способами можно добраться от Октябрьской площади до цирка? Решение. Очевидно, число разных путей от Октябрьской площади до цирка равно 4+3=7. Правило произведения Правило произведения. Пусть некоторый выбор требует выполнения одного за другим
Пример. Из Перми до Чайковского можно добраться теплоходом, поездом, автобусом или самолетом; из Чайковского до Ижевска – теплоходом или автобусом. Сколькими способами можно осуществить путешествие по маршруту Пермь – Чайковский – Ижевск? Решение. Число разных путей из Перми до Ижевска равно Пример. Сколько четырехзначных чисел можно составить из цифр 0,1,2,3,4,5,если: а) ни одна цифра не повторяется больше одного раза в записи числа; б) цифры в записи числа могут повторяться; в) цифры могут повторяться в записи числа, но число должно быть нечетным. Решение. а) Первой цифрой при этом может быть любая из 5 цифр 1,2,3,4,5 (0 не может быть первой цифрой, потому что в таком случае число не четырехзначное). Если первая цифра выбрана, то вторая может быть выбрана 5 способами, третья — 4 способами, четвертая – 3 способами. Согласно правилу произведения общее число способов равно б) Для первой цифры имеем 5 возможностей (1,2,3,4,5), для каждой из следующих цифр – 6 возможностей (0,1,2,3,4,5). Следовательно, общее количество чисел равно в) Первой цифрой может быть одна из 5 цифр 1,2,3,4,5, а последней 1,3,5. Следовательно, общее количество чисел равно Факториал
Размещения.
Например, из 3 элементов Число всех возможных размещений, которые можно образовать из
Пример: Сочетания. Сочетаниями из
Например, из 3 элементов Число всех возможных сочетаний, которые можно образовать из n элементов по k, обозначается символом
(В числителе и знаменателе по Пример: Полезные формулы:
Формула бинома Ньютона Если Часто при решении комбинаторных задач используется биномиальная теорема (бином Ньютона). Биномиальная теорема. Имеет место равенство
Подробнее данная формула расписывается следующим образом: При n =1 имеем тривиальный случай при n =2 и n =3 получаются формулы, хорошо знакомые из школьного курса математики:
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1173; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.73.46 (0.01 с.) |

 способами, а другой элемент
способами, а другой элемент 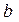 может быть выбран
может быть выбран  способами, причем любой выбор элемента b отличен от любого выбора элемента a, то выбрать либо a, либо b можно
способами, причем любой выбор элемента b отличен от любого выбора элемента a, то выбрать либо a, либо b можно  способами.
способами. способами и после каждого такого выбора элемент
способами и после каждого такого выбора элемент  можно выбрать
можно выбрать  способами, то два элемента (упорядоченную пару)
способами, то два элемента (упорядоченную пару)  и
и 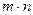 способами.
способами.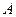 и
и  конечны, то
конечны, то  .
. - конечны, то
- конечны, то .
. ; по условию
; по условию  , тогда по следствию из теоремы 2 имеем.
, тогда по следствию из теоремы 2 имеем. действий. Если первое действие можно выполнить n1 способами, второе (после него) — n2 способами, третье — n3 способами и так до
действий. Если первое действие можно выполнить n1 способами, второе (после него) — n2 способами, третье — n3 способами и так до  способами (после выполнения предыдущих
способами (после выполнения предыдущих  действий), то все
действий), то все  способами.
способами.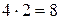 , так как, выбрав любой из четырех возможных способов путешествия из Перми до Чайковского, имеем 2 возможных способа путешествия из Чайковского до Ижевска.
, так как, выбрав любой из четырех возможных способов путешествия из Перми до Чайковского, имеем 2 возможных способа путешествия из Чайковского до Ижевска.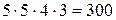 .
. .
. .
. (читается
(читается  . Условились считать, что 0!=1!=1.
. Условились считать, что 0!=1!=1. называются соединения, которые можно образовать из
называются соединения, которые можно образовать из  по 2 можно образовать следующие размещения:
по 2 можно образовать следующие размещения:  .
. и вычисляется по формуле:
и вычисляется по формуле: (всего
(всего  .
.
 :
:

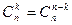 ;
; .
. -е слагаемое) разложения степени бинома обозначать через
-е слагаемое) разложения степени бинома обозначать через  , то
, то  .
. .
. . Это бином Ньютона. Коэффициенты
. Это бином Ньютона. Коэффициенты  называются биномиальными коэффициентами.
называются биномиальными коэффициентами.
 и
и  .
.


