
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события и вероятности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Будем называть испытанием (опытом, наблюдением, измерением) некоторую совокупность действий. Предполагается, в общем случае, что испытание можно повторить неограниченное число раз. Событием (случайным событием) называется всякий факт, который может произойти или не произойти в результате опыта. События обозначаются буквами А, B, C, D, … Вероятностью события называется численная мера возможности появления события в результате данного опыта. Вероятность события А обозначается Р (А). Событие W, которое обязательно произойдет в результате опыта, называется достоверным: Р (W) = 1. Событие Æ, которое никогда не может произойти в результате опыта, называется невозможным: Р (Æ) = 0. Событие А, о котором нельзя заранее сказать произойдет оно или нет в результате опыта, называется случайным: Суммой событий События
Два случайных события называются противоположными, если появление одного из них равносильно не появлению другого. Если одно из этих событий обозначить Формула для вычисления вероятности суммы двух событий, все равно каких, совместных или нет, имеет вид: Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них. Произведением двух событий Если вероятность появления события Если события Событие называется сложным, если появление его зависит от появления других, простых событий. Например, во время броска двух монет событие А – «выпал хотя бы один герб» – сложное событие, потому что оно состоит из таких событий: А1 – «выпал герб только на первой монете»; А2 – «выпал герб только на второй монете»; А3 – «выпал герб на двух монетах»; То есть Несколько событий в данном опыте называются равновозможными, если нет оснований считать какое-либо из них более возможным, чем другое. События
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.131.115 (0.007 с.) |

 .
.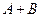 называется событие, состоящее в осуществлении хотя бы одного из событий
называется событие, состоящее в осуществлении хотя бы одного из событий 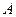 или
или  (безразлично, какого именно, или обоих, если это возможно).
(безразлично, какого именно, или обоих, если это возможно). .
.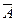 (читается «не
(читается «не  не произошло:
не произошло:  .
. .
. называется событие, состоящее в том, что оба события произошли одновременно. Если появление каждого из событий не зависит от того, произошло или нет другое, то события называются независимыми, и вероятность их произведения равна произведению вероятностей этих событий:
называется событие, состоящее в том, что оба события произошли одновременно. Если появление каждого из событий не зависит от того, произошло или нет другое, то события называются независимыми, и вероятность их произведения равна произведению вероятностей этих событий:  .
. при условии, что событие
при условии, что событие 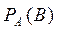 . Вероятность произведения зависимых событий определяется формулой
. Вероятность произведения зависимых событий определяется формулой 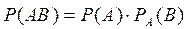 .
. .
.
 называются элементарными, если они образуют полную группу событий, несовместны (то есть никакие два из них не могут произойти одновременно) и равновозможны. Если некоторое событие
называются элементарными, если они образуют полную группу событий, несовместны (то есть никакие два из них не могут произойти одновременно) и равновозможны. Если некоторое событие 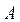 происходит в результате появления одного из элементарных событий
происходит в результате появления одного из элементарных событий  , то эти элементарные события называются благоприятствующими событию
, то эти элементарные события называются благоприятствующими событию  .
.


