
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрическая форма комплексного числаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть Тогда
Последняя запись называется тригонометрической формой комплексного числа. В отличие от нее запись числа в виде Отметим, что тригонометрическая форма – это указание числа по двум его характеристикам: модулю и аргументу. Поэтому вместо формулы (*) можно было бы просто записывать пару Замечание. При записи числа в тригонометрической форме НЕЛЬЗЯ вычислять значения Пример. Запишите в тригонометрической форме числа Решение. Находим модуль, аргумент, а затем выписываем тригонометрическую форму:
Пусть
Заметим, что во внутренних скобках стоят формулы косинуса и синуса суммы аргументов. Поэтому
Последняя запись является тригонометрической формой комплексного числа
иными словами, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Аналогично можно доказать, что
Несложно проверить, что если Используя правило умножения комплексных чисел в тригонометрической форме, получим формулу для возведения комплексного числа в степень Пусть то есть Далее находим Продолжая умножения дальше, придем к формуле
Пример. Вычислите Решение. Находим тригонометрическую форму числа
По формуле Муавра
Переходим к алгебраической форме, вычисляя косинус и синус: Ответ. Тема 1.3 Многочлены Многочлены от одной переменной. Делимость многочленов. Деление многочленов с остатком. Рациональные корни многочленов с целыми коэффициентами. Схема Горнера. Теорема Безу. Число корней многочлена. Многочлены от двух переменных. Формулы сокращенного умножения для старших степеней. Бином Ньютона. Многочлены от нескольких переменных, симметрические многочлены.
Многочленом от переменной Часто будем употреблять и такие термины: Примерами многочленов являются следующие выражения: Многочлен, у которого все коэффициенты равны нулю, называется нулевым. Так, например, многочлен Из записи многочлена видно, что он состоит из нескольких членов. Отсюда и произошел термин ‹‹многочлен›› (много членов). Иногда многочлен называют полиномом. Многочлен от одной переменной Для того чтобы запись многочлена выглядела проще и выглядела компактнее, договорились о ряде условностей. Те члены не нулевого многочлена, у коэффициенты равны нулю, не записывают. Например, вместо
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 787; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.12.236 (0.006 с.) |

 . Положим
. Положим  . Из рисунка 4 очевидно, что
. Из рисунка 4 очевидно, что  .
. . Это выражение запишем в виде
. Это выражение запишем в виде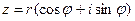 (*)
(*) называют иногда алгебраической формой комплексного числа.
называют иногда алгебраической формой комплексного числа. , но запись (*) принята в силу традиции.
, но запись (*) принята в силу традиции. и
и  , иначе мы потеряем явное указание аргумента
, иначе мы потеряем явное указание аргумента  и снова вернемся к алгебраической форме. Кроме того, если угол
и снова вернемся к алгебраической форме. Кроме того, если угол  получился отрицательным, то знак «–» НЕЛЬЗЯ выносить за знак синуса и НЕЛЬЗЯ убирать его под знаком косинуса.
получился отрицательным, то знак «–» НЕЛЬЗЯ выносить за знак синуса и НЕЛЬЗЯ убирать его под знаком косинуса. .
.


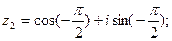


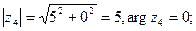
 .
. ,
,  . Найдем произведение
. Найдем произведение 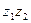 :
:


 , иными словами, при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются.
, иными словами, при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются. , то
, то  .
. , где
, где  ,
, .
. , то есть
, то есть  .
. - эта формула называется формулой Муавра.
- эта формула называется формулой Муавра. , если
, если  .
.
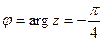 ,
,  .
. .
. .
. будем называть выражение вида
будем называть выражение вида  , где
, где  – любые числа, называемые коэффициентами этого многочлена. Выражения
– любые числа, называемые коэффициентами этого многочлена. Выражения  называются членами многочлена,
называются членами многочлена,  – свободным членом.
– свободным членом. - коэффициент при
- коэффициент при  ,
, 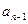 – коэффициент при
– коэффициент при 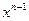 и т.д.
и т.д. . Здесь для первого многочлена коэффициентами являются числа 0, 2, – 3, 3/7; при этом, например, число 2 – коэффициент при
. Здесь для первого многочлена коэффициентами являются числа 0, 2, – 3, 3/7; при этом, например, число 2 – коэффициент при  , а 0 – свободный член.
, а 0 – свободный член. – нулевой.
– нулевой. и т.д. например, если первый приведённых выше многочленов обозначить
и т.д. например, если первый приведённых выше многочленов обозначить  , то можно записать:
, то можно записать:  .
. пишут:
пишут:  ; вместо
; вместо 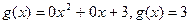 . Таким образом, каждое число – это тоже многочлен. Многочлен
. Таким образом, каждое число – это тоже многочлен. Многочлен  , у которого все коэффициенты равны нулю, т.е. нулевой многочлен, записывают так:
, у которого все коэффициенты равны нулю, т.е. нулевой многочлен, записывают так:  .
.


