
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции с комплексными числамиСодержание книги
Поиск на нашем сайте
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.
Вектор. Линейные операции над векторами Вектором называется направленный отрезок в пространстве, имеющий опред длину. К векторам относится также и нулевой вектор, начало и конец которого совпадают. Единичный- длина к-го равна 1. напр. Может быть какое угодно. Длиной (модулем) вектора называется расстояние между началом и концом вектора. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору. Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему. Линейными операциями над векторами называется сложение и умножение на число. Суммой векторов является вектор -
25 Скалярное произведение векторов, его св-ва и вычисления.Скалярным произведением векторов Свойства скалярного произведения: Первый замечательный предел
В силу четности входящих в неравенство ф-ий, докажем это неравенство на промежутке
2. следовательно, что
1. Покажем, что
2. Докажем, что
3. Последнее утверждение:
Векторное произведение векторов. Свойства. Векторным произведением векторов
j
Свойства векторного произведения векторов: 1) Основные теоремы о пределах Теорема 1. Теорема 2. Теорема 3. Следствие. Теорема 4. Теорема 5. Если f(x)>0 вблизи точки х = а и
Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и Функция f(x) называется ограниченной вблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а. Теорема 7. Если функция f(x) имеет конечный предел при х®а, то она ограничена вблизи точки х = а. Доказательство. Пусть
Второй замечательный предел это форма второго замечательного предела, справедлива и для действ. аргумента lim(n®¥)(1+1/n)n=e
|
|||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 381; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.63.108 (0.008 с.) |

 ;
;  ;2) Умножение.
;2) Умножение. 
 В тригонометрической форме:
В тригонометрической форме:  ,
, 
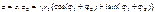 С случае комплексно – сопряженных чисел:
С случае комплексно – сопряженных чисел:  3) Деление.
3) Деление. 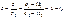

 В тригонометрической форме:
В тригонометрической форме:  4) Возведение в степень.Из операции умножения комплексных чисел следует, что
4) Возведение в степень.Из операции умножения комплексных чисел следует, что
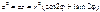 В общем случае получим:
В общем случае получим:  ,где n – целое положительное число. Это выражение называется формулой Муавра.(Абрахам де Муавр (1667 – 1754) – английский математик)Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов. Пример. Найти формулы sin2j и cos2j.Рассмотрим некоторое комплексное число
,где n – целое положительное число. Это выражение называется формулой Муавра.(Абрахам де Муавр (1667 – 1754) – английский математик)Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов. Пример. Найти формулы sin2j и cos2j.Рассмотрим некоторое комплексное число  Тогда с одной стороны
Тогда с одной стороны  .По формуле Муавра:
.По формуле Муавра:  Приравнивая, получим
Приравнивая, получим  Т.к. два комплексных числа равны, если равны их действительные и мнимые части, то
Т.к. два комплексных числа равны, если равны их действительные и мнимые части, то

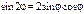 Получили известные формулы двойного угла.5) Извлечение корня из комплексного числа.
Получили известные формулы двойного угла.5) Извлечение корня из комплексного числа.
 Возводя в степень, получим:
Возводя в степень, получим:  Отсюда:
Отсюда: 
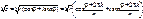
 Произведение -
Произведение -  , при этом
, при этом  коллинеарен
коллинеарен  .Вектор
.Вектор  сонаправлен с вектором
сонаправлен с вектором  (
( противоположно направлен с вектором
противоположно направлен с вектором  тогда
тогда 
 и
и  называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними.  ×
×  = ï
= ï  ïï
ïï  ïcosj
ïcosj ï2;
ï2;  ×
×  = 0, если
= 0, если  ^
^  ×
×  =
=  +
+  ) =
) =  ;(m
;(m  в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то  ×
×  = xa xb + ya yb + za zb; Используя полученные равенства, получаем формулу для вычисления угла между векторами:
= xa xb + ya yb + za zb; Используя полученные равенства, получаем формулу для вычисления угла между векторами:  ; Пример. Найти (5
; Пример. Найти (5  ), если
), если  10
10  ×
×  + 6
+ 6  , т.к.
, т.к. 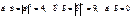 .
. Доказательство: докажем для
Доказательство: докажем для  справедливость неравенства
справедливость неравенства 
 Из рисунка видно, что площадь кругового сектора
Из рисунка видно, что площадь кругового сектора
 , так как х >0, то
, так как х >0, то  ,
,








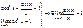
 называется вектор
называется вектор  , удовлетворяющий следующим условиям:1)
, удовлетворяющий следующим условиям:1)  , где j - угол между векторами
, где j - угол между векторами  2) вектор
2) вектор  ортогонален векторам
ортогонален векторам 
 3)
3)  или
или  .
.

 ;2)
;2)  , если
, если  ïï
ïï  )´
)´  =
=  ) =
) =  (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами
(xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами  , то
, то  6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах 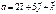 и
и  .
.  .
. , где С = const.Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.
, где С = const.Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а. Доказательство этой теоремы будет приведено ниже.
Доказательство этой теоремы будет приведено ниже.

 при
при 
 , то А>0. Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.
, то А>0. Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0. , то и
, то и  .
. , т.е.
, т.е.  , тогда
, тогда или
или  ,.е.
,.е.  где М = e + ïАïТеорема доказана.
где М = e + ïАïТеорема доказана.


