
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечно малые и бесконечно большие функции. Их свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если Теорема. Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие f(x) = A + a(x), где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а). Свойства бесконечно малых функций: 1.Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а. 2.Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а. 3.Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а. 4.Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая. Бесконечно большие функции Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенствоïf(x)ï>M выполняется при всех х, удовлетворяющих условию0 < ïx - aï < D Записывается Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим: Функция называется бесконечно большойпри х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой. Теорема. Если f(x)®0 при х®а (если х®¥) и не обращается в ноль, то Предел функции на бесконечности Пусть функция f(x) определена на (a, + ∞). Число A называется пределом функции f(x) при x → + ∞ (обозначается A = lim x → + ∞ f(x)), если ε > 0 N: x > N |f(x) − a| < ε. Пусть функция f(x) определена на (− ∞,a). Число A называется пределом функции f(x) при x → − ∞ (обозначается A = lim x → − ∞ f(x) }, если ε > 0 N: x < − N |f(x) − a| < ε. Если существуют пределы функции f(x) при x → + ∞ и при x → − ∞ и они равны одному и тому же числу A, то это число A называется пределом функции f(x) при x → ∞ {обозначается A = lim x → ∞ f(x). Теоремы о пределах последовательностей и правила их вычисления распространяются и на пределы функций в бесконечности.
Предел функции в точке Пусть функция f(x) определена в некоторой проколотой окрестности точки x0. Число A называется пределом функции f(x) при x → x0 (или в точке x0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < |x − x0| < δ, справедливо неравенство |f(x) − A| < ε, т.е. lim x → x0 f(x) = A ε > 0 δ > 0: 0 < |x − x0| < δ |f(x) − A| < ε. Используем понятие окрестности и учтем, что 0 < |x − x0| < δ x • O δ (x0) и |f(x) − A| < ε f(x) Oε (A). (Точка над символом окрестности указывает, что это проколотая окрестность.) Теперь определение предела функции в точке можно представить в виде lim x → x0 f(x) = A ε > 0 δ > 0: x • Oδ (x0) f(x) Oε (A).
10. Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью.
Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
Сопряжённые комплексные числа имеют одинаковый модуль. __ Аргумент комплексного числа - это угол Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a + bi можно выразить через его модуль r и аргумент
|
||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 820; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 .Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.
.Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет. .
.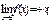 а если заменить на f(x)<M, то:
а если заменить на f(x)<M, то: 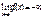
 , где А – число или одна из величин ¥, +¥ или -¥.
, где А – число или одна из величин ¥, +¥ или -¥.



 между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan
между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan 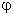 :
:



