
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отображение бесконечно малой сфероидической трапеции на плоскости.Содержание книги
Поиск на нашем сайте
Бесконечно малая сфероидическая трапеция ABCD эллипсоида (рис 6.2) отображается на плоскость бесконечно малой косоугольной трапецией Элементами этого изображения являются: бесконечно малые отрезки изображения меридиана
Линейный элемент. Рис. 6.3. Элементы изображения бесконечно малой сфероидической трапеции. Из рис (6.3) имеем:
Определим значения cosi и sini. Для этого вначале составим функцию При этом из двух знаков перед корнем берётся знак плюс, так как в математической картографии всегда используется только положительное значение h. Теперь, если записать:
В этих формулах угол i считается северо-восточным в том же направлении, как идёт счёт азимутов. Его четверть определяется знаком при величине f. Если f>0, то Если f<0, то При f=0,угол Таким образом, выражение является условием ортогональности картографической сетки на проекции. Поскольку сетка часто изображается не ортогонально, то нередко возникает вопрос о величине отклонения угла i от прямого. Обозначим
выражение (6.37) устанавливает связь азимутов
Площадь изображения бесконечно малой трапеции на проекции. Для бесконечно малого параллелограмма можно записать: Используя выражения (6.25) и (6.34) получаем равенство:
Теория искажений.
Масштабы и искажения. Растяжение и сжатие отдельных частей изображения картографируемой поверхности в той или иной картографической проекции неизбежно сопровождаются искажениями длин, площадей и углов, причём эти искажения зависят от свойств изображения. Каждая карта имеет главный масштаб, который показывает общую степень уменьшения всей картографируемой поверхности при её отображении на плоскости. Этот масштаб подписывается на карте, но сохраняется только в отдельных точках или на некоторых линиях карты. При исследовании картографических проекций главный масштаб, обозначаемый Поскольку масштаб на карте является величиной переменной, в практику вводится понятие частных масштабов длин и площадей в данной точке по данному направлению. Частным масштабом длин Частный масштаб длин является функцией географических координат, определяющих положение точки на картографируемой поверхности, и азимута направления, по которому определяется частный масштаб, В дальнейшем частные масштабы для простоты изложения будем называть масштабами вдоль каких-либо направлений. Например, масштаб по меридианам. Искажение длин т.е. искажение длин может быть положительным и отрицательным. Частный масштаб длин отрицательным быть не может, в случае Частным масштабом площади (р) называется отношение бесконечно малого (элементарного) участка на карте Как правило, Частный масштаб площади зависит только от географического положения изображаемой точки: В дальнейшем будем называть частный масштаб площади просто масштабом площади. Искажение площади В некоторых случаях искажения длин и площадей характеризуют отвлечённой величиной, выраженной разностями Третий вид искажений – искажения углов; они характеризуются разностью между величиной угла в проекции Как правило, Искажение углов: является функцией географических координат и азимутов направлений В каждой точке проекции имеют место максимальные искажения углов, обозначаемые где Величина искажений является одним из основных критериев оценки достоинства картографических проекций.
Вывод общей формулы частного масштаба длин. Масштабы по меридианам и параллелям. Частный масштаб длин по формуле (6.28)
В последней формуле использованы коэффициенты Гаусса:
и подставим в формулу (6.44),
Для шара
Не трудно видеть из выражений (6.47) – (6.51), что частные масштабы длин по любому направлению зависят от координат точек и азимутов направлений линейных элементов.
Экстремальные значения частных масштабов длин, главные направления. Продифференцируем формулу (6.51) по Тогда Поскольку период тангенса равен Эти направления ортогональны и называются главными, при этом экстремальные масштабы обозначаются буквами а – наибольший и b – наименьший масштабы. Применяя теоремы Апполония, можем найти формулу связи экстремальных масштабов с масштабами по меридианам и параллелям.
Теорема 1. Сумма квадратов сопряжённых полудиаметров эллипса – величина постоянная, равная сумме квадратов его полуосей:
Теорема 2. Площадь параллелограмма, построенного на сопряжённых полудиаметрах эллипса, - величина постоянная, равная площади прямоугольника, построенного на его полуосях:
Решим приведённые уравнения совместно (умножив предварительно обе части последнего уравнения на два): и введём новые обозначения А и В: Тогда исходные экстремальные масштабы
Эллипс искажений. Наибольшие искажения углов. Пусть на эллипсоиде взята бесконечно малая трапеция ABCD, которую с достаточной точностью принимаем за плоский бесконечно малый прямоугольник (рис.6.5).
Рис. 6.6. Схема построения эллипса искажений. Установим в каждой точке на поверхности эллипсоида, например, в точке А системы координат
Учитывая значения частных масштабов длин вдоль меридианов: и параллелей: выражение (6.55) на плоскости принимает вид: Отсюда следует, что в общем случае бесконечно малая ок5ружность (6.55) на поверхности эллипсоида (сферы) изображается на плоскости бесконечно малым эллипсоидом (6.56).
Из формулы (6.56) также следует, что в частных случаях, а именно в равноугольных проекциях, в которых частные масштабы длин вдоль меридианов и параллелей равны (m=n), бесконечно малая окружность на поверхности эллипсоида (сферы) изображается на плоскости подобной бесконечно малой окружностью. Эллипсом искажений или индикатрисой (указательницей) Тиссо назвали эллипс конечных размеров (например, при радиусе окружности (6.55) R=1), соответствующий бесконечно малому эллипсу (6.56). Для его построения достаточно вычислить в заданной точке значения частных масштабов длин m,n или a,b и углов i (или Теперь из рис.6.5 и 6.6 запишем значения углов на эллипсоиде (сфере) и проекции от главных направлений: а также искажения углов на проекции: Используя значения экстремальных частных масштабов длин нетрудно определить формулу связи этих углов: Это позволяет представить азимуты линейных элементов в виде: Составим отношение: Подставим в это соотношение значение v из выражения (6.58): Обозначим по В.В. Витковскому наибольшие искажения углов
Частные масштабы площадей. Из определения частного масштаба площадей На картографируемой поверхности площадь элементарной трапеции, ограниченной бесконечно малыми дугами меридианов и параллелей (рис6.7),
На плоскости (рис.6.7) Тогда масштаб площадей Используя формулу (6.53) получим Известно, что В приведённых формулах частный масштаб площадей выражен через частные масштабы длин. Если в формулу (6.61) подставить значения частных масштабов длин и синуса угла между меридианами и параллелями, то формула частного масштаба площадей примет вид:
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.24.110 (0.008 с.) |

 (рис 6.3), которую с точностью до членов более высоких порядков малости можно принять за бесконечно малый параллелограмм, а её линейный элемент
(рис 6.3), которую с точностью до членов более высоких порядков малости можно принять за бесконечно малый параллелограмм, а её линейный элемент  - за бесконечно малый отрезок прямой.
- за бесконечно малый отрезок прямой. и параллели
и параллели 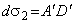 , которые образуют с осью абсцисс Х соответственно углы
, которые образуют с осью абсцисс Х соответственно углы  , линейный элемент
, линейный элемент  , составляющий с осью Х угол
, составляющий с осью Х угол  ; азимут линейного элемента
; азимут линейного элемента  ; углы i в точках проекции между изображениями меридианов и параллелей и площадь изображения малой сфероидической трапеции
; углы i в точках проекции между изображениями меридианов и параллелей и площадь изображения малой сфероидической трапеции  .
.


 . Используя коэффициенты Гаусса (6.24) получим:
. Используя коэффициенты Гаусса (6.24) получим:

 - угол лежит в первой четверти.
- угол лежит в первой четверти. - угол лежит во второй четверти.
- угол лежит во второй четверти. - меридианы и параллели изображаются ортогональными линиями.
- меридианы и параллели изображаются ортогональными линиями. (6.35)
(6.35) , тогда из формулы (6.31):
, тогда из формулы (6.31): (6.36)
(6.36)
 линейных элементов на плоскости и на поверхности эллипсоида.
линейных элементов на плоскости и на поверхности эллипсоида. .
.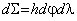 (6.37)
(6.37) , обычно принимают за единицу, т.к. он не влияет на свойства используемой картографической проекции.
, обычно принимают за единицу, т.к. он не влияет на свойства используемой картографической проекции. называется отношение бесконечно малого отрезка в проекции
называется отношение бесконечно малого отрезка в проекции  к соответствующему бесконечно малому отрезку на картографируемой поверхности
к соответствующему бесконечно малому отрезку на картографируемой поверхности  .
. (6.38)
(6.38)
 называется разность между частным масштабом и единицей, выраженная в процентах, например:
называется разность между частным масштабом и единицей, выраженная в процентах, например:
 изображение пропадёт.
изображение пропадёт. к соответствующему участку на картографируемой поверхности
к соответствующему участку на картографируемой поверхности  .
.
 , но могут существовать такие проекции, в каждой точке которых
, но могут существовать такие проекции, в каждой точке которых  , - равновеликие проекции.
, - равновеликие проекции.
 называется разность между масштабом площади и единицей, выраженная в процентах, например:
называется разность между масштабом площади и единицей, выраженная в процентах, например:
 ,
,  или логарифмом масштаба
или логарифмом масштаба  , при разложении которого в ряд первым (главным) членом разложения будет разность
, при разложении которого в ряд первым (главным) членом разложения будет разность  и величиной соответствующего угла на картографируемой поверхности
и величиной соответствующего угла на картографируемой поверхности  .
. , но могут существовать такие проекции, в каждой точке которых
, но могут существовать такие проекции, в каждой точке которых  , - равноугольные проекции.
, - равноугольные проекции.
 .
. :
: ,
, в проекции по указанному направлению.
в проекции по указанному направлению.



 ) приравняем нулю.
) приравняем нулю. (6.52)
(6.52) , это уравнение даёт два корня
, это уравнение даёт два корня  , т.е. даёт значения азимутов двух направлений, по которым частные масштабы длин экстремальны.
, т.е. даёт значения азимутов двух направлений, по которым частные масштабы длин экстремальны.
 (6.53)
(6.53)

 (6.54)
(6.54)

 и
и  и соответствующих точках плоскости – системы
и соответствующих точках плоскости – системы  и
и  , в которых оси направлены вдоль меридианов, параллелей и по главным направлениям. Проведём вокруг точки А на поверхности эллипсоида (сферы) окружность радиусом R=AC:
, в которых оси направлены вдоль меридианов, параллелей и по главным направлениям. Проведём вокруг точки А на поверхности эллипсоида (сферы) окружность радиусом R=AC: (6.55)
(6.55) ;
;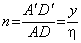 ,
, (6.56)
(6.56) ) и
) и 
 (6.57)
(6.57) ,
, (6.58)
(6.58) (6.59)
(6.59)

 и учитывая, что наибольшие их величины будут при
и учитывая, что наибольшие их величины будут при  , получаем:
, получаем: (6.60)
(6.60)
 .
.
 (6.61)
(6.61) .
. , поэтому
, поэтому (6.62)
(6.62) (6.63)
(6.63)


