
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия равноугольного, равновеликого и равнопромежуточногоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Отображения эллипсоида на плоскости.
Условия равноугольного отображения. Основным условием равноугольного отображения является подобие в бесконечно малых частях, а следовательно, независимость масштаба длин от направления. Если же масштаб длин не зависит от направления, то его производная по азимуту Это равенство соблюдается только в том случае, когда Q=0 и P=R. В соответствии с формулами (6.46) или Следовательно, в равноугольных проекциях картографическая сетка ортогональна, масштаб не зависит от направления m=n=a=b и углы не искажаются, т.е. Если в формулы (6.64) подставить значения e, f, g, то Получив значение получив значение В полученных уравнениях выберем знаки, при которых величина h будет иметь положительное значение. Окончательный вид уравнений равноугольных проекций, называемых уравнениями Коши-Римана:
Условия равновеликого отображения. При равновеликом отображении сохраняется постоянным отношение площади на карте к соответствующей площади на картографируемой поверхности. Масштаб площадей в этом случае p=const=1. Из формулы (6.63) отсюда для эллипсоида h=Mr (6.66) (для p=const, h=kMr, где k – постоянный коэффициент), для поверхности шара
Условия равнопромежуточного отображения. Равнопромежуточными называются проекции, сохраняющие длины по одному из главных направлений. Наиболее часто к ним относят проекции с ортогональной картографической сеткой. В этих случаях главными будут направления вдоль меридианов и параллелей. Соответственно определяются равнопромежуточные проекции вдоль одного из этих направлений.
В равнопромежуточных проекциях вдоль меридианов должно выполняться тождество: Отсюда искомые условия принимают вид: где М определяется по (6.10)
В равнопромежуточных проекциях вдоль параллелей соответственно должно выполняться тождество: Отсюда с учётом (6.49) рассматриваемые условия равнопромежуточности принимают вид: Аналогично при отображении поверхности шара имеем:
О распределении искажений на картографических проекциях. Пи выборе и использовании картографических проекций необходимо добиваться, чтобы на созданных картах обеспечивались минимальные искажения и лучше их распределения в пределах изображаемой территории. Известно, что всякая функция вблизи своего экстремума изменяется медленнее, чем малые изменения аргументов. Применительно к картографическим проекциям назовём центральную линию и точку, в которых искажения длин, углов, азимутов и площадей проходят через свой экстремум (минимум). Следовательно, в окрестностях центральной линии или центральной точки искажения на проекции будут изменяться медленно. Отсюда выбор или изыскание проекции для создания карты на конкретные территории необходимо осуществлять под условием, чтобы центральная точка проекции располагалась примерно в средней точке изображаемой области, а центральная линия находилась в середине и была направлена вдоль наибольшего распространения картографируемой территории. Учитывая свойства картографических проекций центральными являются: - в цилиндрических проекциях – изображение линии экватора нормальной или косой (поперечной) систем координат; - в канонических проекциях – линия изображения средней параллели; - в азимутальных проекциях – точка полюса.
В настоящее время для характеристики искажений в отдельных точках проекции наиболее часто используют изоколы – линии равных искажений, которые дают наглядное представление о величине и распределении различных искажений на карте.
Классификация картографических проекций.
Рассмотрим классификацию проекций по трём основным признакам: по характеру искажений (свойствам изображения); по виду нормальной сетки меридианов и параллелей и в зависимости от положения точки полюса принятой системы координат.
Классификация картографических проекций По характеру искажений.
По характеру искажений проекции делятся на - равноугольные - равновеликие - произвольные. В равноугольных проекциях сохраняется подобие бесконечно малых частей изображения, следовательно, частный масштаб длин не зависит от направления Условия равноугольности имеют вид f=0;m=n или для поверхности шара При изображении в равноугольных проекциях участков конечного размера изменения частных масштабов длин обуславливает искажение конечных контуров. В этих проекциях обычно сильно искажаются площади. В равноугольных проекциях сохраняется постоянным отношение площадей на картографируемой поверхности и на плоскости. При этом постоянство отношений площадей распространяется не только на бесконечно малые участки, но и на участки конечных размеров. В этих проекциях частный масштаб площадей но чаще всего р=1, поэтому условие равновеликости имеет вид h=Mr, а для поверхности шара Экстремальные масштабы длин обратно пропорциональны друг другу: a=1/b; b=1/a. Максимальное искажение углов целесообразно вычислять по формулам тангенсов, которые в равновеликих проекциях принимают вид Если картографическая проекция не обладает ни свойством равноугольности, ни свойством равновеликости, то она относится к группе произвольных. В этих проекциях искажаются углы и площади. Среди произвольных проекций следует выделить проекции равнопромежуточные, в которых сохраняется постоянным экстремальный масштаб длин по одному из главных направлений, т.е. а=1 или b=1. В этих проекциях соответственно p=b или p=a. Для вычислений максимального искажения углов целесообразно использовать общую формулу Классификация проекций по виду нормальной сетки меридианов и параллелей. Нормальной сеткой называется сетка меридианов и параллелей, которая получается в случае, когда полюс используемой системы координат совпадает с географическим полюсом; проекции с такой сеткой называют нормальными. По виду нормальной сетки картографические проекции подразделяются на две группы. а) Проекции с параллелями постоянной кривизны, б) проекции с параллелями переменной кривизны. Здесь рассмотрим проекции только первой группы. Проекции с постоянной кривизной параллелей подразделяются в свою очередь на: · проекции, в которых параллели изображаются прямыми линиями; · проекции, в которых параллели изображаются концентрическими окружностями; · проекции, в которых параллели изображаются эксцентрическими окружностями. Примером первого семейства проекций служат цилиндрические и псевдоцилиндрические проекции.
Нормальные цилиндрические проекции (рис. 7.1) имеют наиболее простую картографическую сетку; меридианы изображаются в них равноотстоящими параллельными прямыми, а параллели – параллельными прямыми, ортогональными меридианам.
В псевдоцилиндрических проекциях (рис. 7.2) параллели – прямые линии перпендикулярные к прямолинейному осевому меридиану, остальные меридианы – кривые (синусоиды, эллипсы), симметричные относительно осевого. Сетка проекций неортогональна, поэтому по характеру искажений псевдоцилиндрические проекции могут быть только равновеликими и произвольными.
К числу проекций второго семейства относят конические, псевдоконические проекции, азимутальные и псевдоазимутальные. Нормальными коническими называют проекции (рис. 7.3), в которых картографическая сетка имеет следующий вид: меридианы – прямые, сходящиеся в одной точке под углами, пропорциональными разности долгот соответствующих меридианов, а параллели – дуги концентрических окружностей, центр которых находится в точке схода меридианов.
В проекциях псевдоконических (рис. 7.4) нормальная сетка имеет следующий вид: параллели — дуги концентрических окружностей, а меридианы — кривые, симметричные относительно осевого прямолинейного. Сетка проекции неортогональна, поэтому по характеру искажений эти проекции могут быть только равновеликими и произвольными.
В азимутальных проекциях (рис. 7.5) меридианы нормальной сетки — прямые, пересекающиеся в одной точке под углами, равными разности долгот соответствующих меридианов, параллели — концентрические окружности с центром в точке пересечения меридианов.
В псевдоазимутальных проекциях (рис.7.6) - проекциях с овальными изоколами. Параллели являются концентрическими окружностями, а меридианы кривыми, за исключением двух, взаимно перпендикулярных, которые служат осями симметрии.
Третье семейство включает два класса а) Поликонические проекции в широком смысле (рис 7.7),в которых параллели эксцентрические окружности, центры которых находятся на среднем меридиане, а меридианы кривые симметричные относительно среднего прямолинейного меридиана. б) Поликонические проекции в узком смысле. Для этих, проекций дополнительно к предыдущему определению накладываются два условия: полярный радиус частный масштаб длин на среднем меридиане имеет постоянное значение
РИС. 7.7. Поликоническая проекция
Классификация проекций в зависимости от положения точки полюса принятой системы координат Кроме нормальных проекций существуют проекции косые и поперечные. В основу этого подразделения положено значение широты полюса сферической системы координат ( В нормальных проекциях нормальная сетка совпадает с основной, т. е. с сеткой параллелей и меридианов, положение которых на картографируемой поверхности характеризуется географическими координатами ( В косых и поперечных проекциях нормальная сетка не совпадает с основной. Нормальной сеткой в этих проекциях является сетка вертикалов и альмукантаратов. Вертикалы являются большими кругами, пересекающимися в точках полюсов косой или поперечной системы Положение вертикалов на картографируемой поверхности определяется азимутом а, который равен двугранному углу между плоскостями текущего и начального вертикалов. Начальным называется вертикал, который совпадает с меридианом полюса косой или поперечной системы координат, т. е. имеет долготу
Альмукантараты — малые круги, перпендикулярные к вертикалам; их положение на картографируемой поверхности определяется координатой z— зенитным расстоянием, которое равно дуге вертикала от полюса нормальной системы координат Q до текущего альмукантарата. Сетку вертикалов и альмукантаратов можно рассматривать как смещенную сетку меридианов и параллелей, в которой географический полюс Р заменен полюсом косой или поперечной системы координат Q Вычисление косых и поперечных проекций выполняют по следующей схеме. 1). Картографируемою поверхность, как правило, принимают за поверхность шара радиусом R, значение которого находят в соответствии с заданными условиями или считают равным радиусу кривизны картографируемой области. 2). Определяют координаты 3). Выполняют переход от географических координат к сферическим полярным координатам косой или поперечной систем по известным формулам сферической тригонометрии: 4). Далее вычисляют прямоугольные координаты Далее в главе более полно рассмотрены некоторые классы проекций из числа наиболее часто встречающихся в практике картографирования. К ним относятся: цилиндрические, конические, азимутальные (как частный случай конических проекций), перспективно-азимутальные проекции. Кроме того рассмотрены проекции основных видов карт: топографических и обзорных общегеографических карт России и сопредельных государств. ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ
|
|||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.37.122 (0.013 с.) |

 будет равна нулю.
будет равна нулю.
 (6.64)
(6.64)
 .
.
 из первого уравнения и подставив его во второе, найдём:
из первого уравнения и подставив его во второе, найдём:
 , найдём
, найдём .
. (6.65)
(6.65)
 .
. (6.67)
(6.67)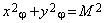 , (6.68)
, (6.68) (6.69)
(6.69) (6.70)
(6.70)
 , искажения углов отсутствуют
, искажения углов отсутствуют  , масштаб площади равен квадрату масштаба длин
, масштаб площади равен квадрату масштаба длин  .
.

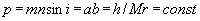 ,
, .
.
 . Если сетка равнопромежуточной проекции ортогональна и главные направления совпадают с меридианами или параллелями, проекции называют соответственно равнопромежуточными по меридианам или параллелям.
. Если сетка равнопромежуточной проекции ортогональна и главные направления совпадают с меридианами или параллелями, проекции называют соответственно равнопромежуточными по меридианам или параллелям.


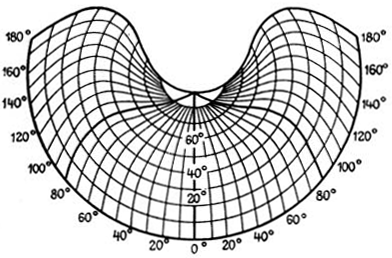

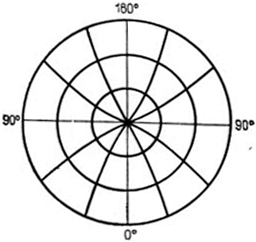
 ;
; .
.
 ). При
). При  ).
). .
. (рис.7.8)
(рис.7.8) РИС.7.8 Сферические координаты z и а косой системы
РИС.7.8 Сферические координаты z и а косой системы
 (7.1)
(7.1) (7.2)
(7.2)



