
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая теория картографических проекций.Содержание книги
Поиск на нашем сайте
Элементы геодезической основы, используемые при создании карт. К элементам геодезической основы относят опорные пункты, определённые в системе геодезических координат, принятые в данном государстве, и координатные сетки, связанные с этими опорными пунктами. Геодезические системы координат включают: - параметры референц-эллипсоида (величина большой полуоси а или малой b, сжатие - высоту геоида над референц-эллипсоидом в начальном пункте; - исходные геодезические даты (геодезическая широта и долгота начального пункта, азимут на геометрический пункт).
В работах по геодезии, топографии и картографии, выполняемых в России, используется эллипсоид Красовского (а=6378245м, Принята Балтийская система высот. Счёт высот в этой системе ведётся от нуля Кронштатского футштока. При создании карт на российские дальневосточные регионы иногда применяется система высот Охотского моря. В процессе выполнения картосоставительских работ определяют геодезическую систему координат и систему высот, которые приняты при создании исходного картографического материала. При отсутствии данных о системе геодезических координат, которая была принята при создании исходного картографического материала, её можно установить, если имеется хотя бы три пункта в системе координат исходного материала. При этом можно воспользоваться графическим способом преобразования геодезической системы координат исходного картографического материала в геодезическую систему координат создаваемой карты. Для этого на прозрачный пластик в масштабе создаваемой карты наносят координатную сетку, углы рамок трапеции и геодезические пункты в принятой для создания карты системе геодезических координат, изображение которых имеется на исходном картографическом материале. Этот пластик накладывают на исходный картографический материал. Совместив идентичные пункты пластика и исходного материала, устанавливают имеются ли смещения координатных сеток и углов рамок трапеции на пластике относительно изображения на картографическом материале. Отсутствие таких смещений свидетельствует о том, что исходный картографический материал и создаваемая карта имеют единую систему координат.
Если такие смещения имеются, то с пластика перекалывают на исходный материал углы рамок трапеции и координатную сетку. Более строго это задача решается аналитически – путём введения так называемых дифференциальных поправок первого и второго рода.
Системы координат. Установим систему декартовых прямоугольных пространственных координат следующим образом. Начало координат поместим в центре эллипсоида, ось z направим вдоль оси вращения, ось х – в плоскости, перпендикулярной к оси вращения, ось у дополняет систему координат до правой (рис.6.1)
Из аналитической геометрии известно, что в этой системе координат уравнение поверхности эллипсоида вращения. Умножив его на Возьмём плоскость z=const. Найдём след пересечения поверхности эллипсоида этой плоскостью. Совместное решение уравнений этой плоскости и поверхности эллипсоида даст нам уравнение окружности. Таким образом, плоскости z=const в пересечении с поверхностью эллипсоида дают окружности. Эти окружности называются параллелями r=const. Параллель с наибольшим радиусом r=a (z=0) называется экватором. Экватор делит эллипсоид на две симметричные половины. Пересекая поверхность эллипсоида вращения плоскостями, проходящими через ось вращения, получим совершенно одинаковые кривые – эллипсы. Половина каждого эллипса, расположенная между полюсами, называется меридианом. Если в уравнении (6.1) исключим координаты х и у по равенству (6.3), то получим уравнение меридиана Параллели и меридианы можно принять в качестве системы ортогональных координатных линий на эллипсоиде. Это возможно, так как каждая параллель пересекается с каждым меридианом под прямым углом, а их пересечение определяет положение единственной точки на поверхности данного полусфероида. Исключение составляют полюсы Р и Примем один из меридианов за начальный. Тогда положение любого меридиана будет определятся двугранным углом, составленным плоскостью начального меридиана и плоскостью данного меридиана. Он обозначается буквой L и называется геодезической долготой.
Долготы, отсчитываемые от плоскости начального меридиана к востоку (в полюсе – против движения часовой стрелки) в пределах от 0 до долготами. Таким образом, меридиан есть координатная линия, во всех точках которой геодезическая долгота имеет одну и ту же величину (L=const). Перейдём к установлению координаты для параллели. В некоторой точке Q (рис. 6.1) проведём главную нормаль меридиана, которая пересечёт ось вращения в точке n. Острый угол, составленный нормалью к поверхности эллипсоида и плоскостью экватора, называется геодезической широтой и обозначается буквой В. Геодезическая широта отсчитывается от плоскости экватора в пределах от 0 до Таким образом, параллель есть координатная линия, во всех точках которой геодезическая широта имеет одну и ту же величину (B=const). Система геодезических координат B и L представляют собой главную систему координат, позволяющую однозначно определять положение любой точки на поверхности эллипсоида. Она широко применяется в геодезии и картографии. Практическое значение её заключается в том, что геодезические координаты B и L незначительно отличаются от астрономических координат В современной теории картографических проекций геодезические координаты называют географическими, используя исторически сложившиеся обозначения
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.141.201 (0.008 с.) |

 или эксцентриситет е);
или эксцентриситет е);
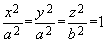 (6.1)
(6.1) , получим другой вид уравнения поверхности эллипсоида вращения:
, получим другой вид уравнения поверхности эллипсоида вращения: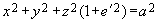 (6.2)
(6.2)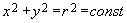 , (6.3) где r – радиус окружности.
, (6.3) где r – радиус окружности. (6.4)
(6.4) , в которых сходятся все меридианы.
, в которых сходятся все меридианы. называют восточными долготами, а к западу в пределах от 0 до
называют восточными долготами, а к западу в пределах от 0 до  - западными
- западными . Для точек, расположенных в северном полусфероиде, её принято считать положительной, а в южном – отрицательной.
. Для точек, расположенных в северном полусфероиде, её принято считать положительной, а в южном – отрицательной. , определяемых астрономическими методами независимо от геодезических измерений.
, определяемых астрономическими методами независимо от геодезических измерений.


