
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гномонические, стереографические и ортографические проекцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гномоническая проекция В этой проекции точка зрения расположена, в центре сферы. Подставив значение D = 0 в формулы (7.17), получим Линией кратчайшего расстояния (ортодромией) на сфере является дуга большого круга. Так как центр такой окружности совпадает с центром сферы, а значит, с точкой проецирования в гномонической проекции, то ортодромия изображается в проекции прямой линией.
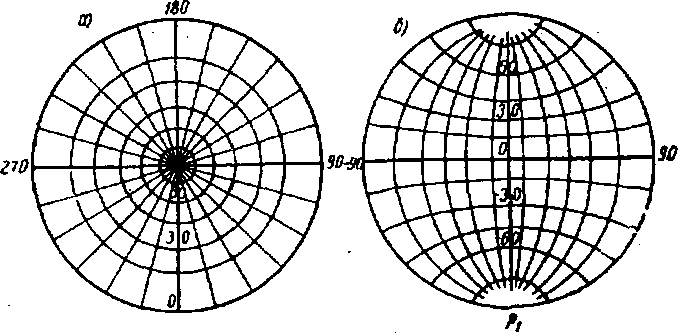
РИС.7.18. Гномоническая проекция: а— поперечная
Стереографическая проекция
В этой проекции точка проектирования расположена на сфере, т. е. D = R. Тогда 'по формуле (7.16) Общие формулы проекции: Стереографическая проекция идентична равноугольной азимутальной. Стереографическая проекция обладает важным свойством — любая окружность конечных размеров на сфере изображается в проекции окружностью. Ортографическая проекция В этой проекции точка проектирования находится в бесконечности (D = Если разделить числитель и знаменатель дроби в формуле (7.16) на D, то получим Тогда формулы ортографической проекции: Так как частный масштаб а) 180
Проекции топографических карт
Все рассмотренные выше проекции можно представить как проекции сплошного изображения картографируемой поверхности в переменном масштабе. Проекции топографических карт должны сохранять постоянство масштаба в пределах графической точности на всей картографируемой поверхности. С этой целью поверхность делят на участки. Схематично изображение в проекции топографических карт можно представить как результат проектирования каждого участка поверхности на вспомогательную поверхность цилиндра или конуса с последующим развертыванием её на плоскость (рис. 7.21). При этом переход на плоскость совершается путем применения какой-либо целесообразно выбранной проекции.
Проекция должна обладать свойствами равноугольности, так как, сохраняя подобие в бесконечно малых частях, равноугольная проекция обуславливает практическое постоянство масштаба по всем направлениям в пределах некоторого малого участка, для которого эта точка является центральной.
Участки могут иметь форму трапеции (карта масштаба 1:1000000), широтного пояса (рис. 7.22) или меридианальной зоны (рис. 7.23). Величину участка определяет требуемая точность изображения в заданном масштабе.
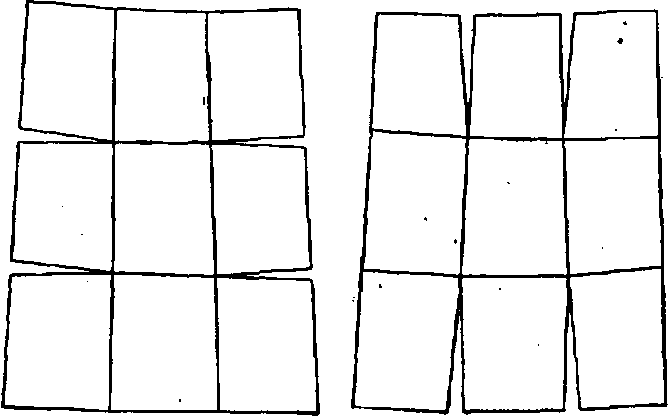
Для отечественных топографических карт масштабов 1:1000 000 и крупнее применяется поперечно-цилиндрическая проекция Гаусса-Крюгера. (Эту проекцию в литературе также называют проекцией Гаусса). Таким образом, можно изобразить всю земную поверхность, но, развернув на плоскость, получим «разрывы» между отдельными участками (рис. 7.24). Теоретически возможно соединить на плоскости колонку трапеций, идущих с юга на север, или пояс трапеций, идущих с запада на восток, но нельзя без разрывов соединить два смежных пояса или две смежные колонки трапеций. На рис. 7.24 показаны разрывы, возникшие при склейке девяти трапеций. Величина углового разрыва где
Рис. 7.24 Угловые разрывы при склейке девяти трапеций
Проекция Гаусса-Крюгера Проекция применяется для отечественных карт масштабов 1:1000 000 и крупнее. Проекция Гаусса - Крюгера является проекцией эллипсоида на плоскость, и ее определяют следующие условия: — равноугольность изображения; — изображение осевого (среднего) меридиана в виде прямой, по отношению к которой все меридианы и параллели располагаются симметрично; — сохранение длины осевого меридиана.
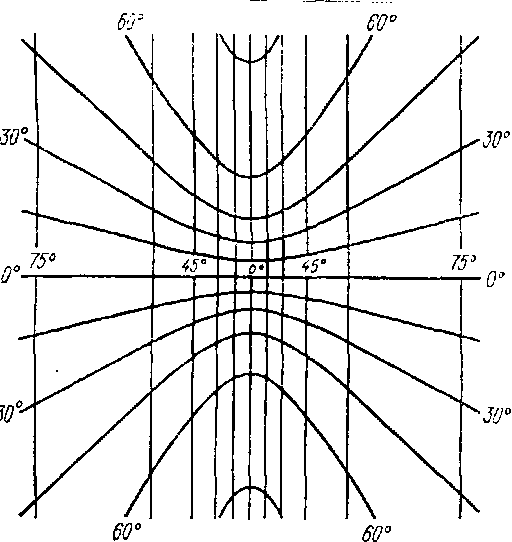
Рис. 7.25. Картографическая сетка проекции Гаусса —Крюгера
Проекция Гаусса при сплошном изображении больших территорий, вытянутых по долготе, дает большие искажения. Поэтому в целях уменьшения искажений она применяется по зонам, ограниченным линиями меридианов. Каждая зона изображается на плоскости отдельно, причем за ось Х принимается изображение среднего (осевого) меридиана каждой зоны, а за ось Y — изображение экватора. Протяженность зон по долготе берется такой, чтобы искажения на их краях были пренебрегаемо малы. При удалении к западу или востоку от осевого меридиана на 3° относительное искажение длин достигает на экваторе 1/750, а на широте 45° — 1/1500. Такое искажение допустимо для карт масштабов 1:25000 и мельче. Получим уравнение проекции Гаусса – Крюгера. На основании общего уравнения равноугольных проекций где q и но Приравняв действительные и мнимые части последнего равенства, получим общие уравнения равноугольных проекций: Величина F (q) называется характеристикой; в проекциях, где картографические сетки симметричны осевому меридиану, она характеризует абсциссу проекции на этом меридиане. Т.к. длина осевого меридиана изображается без искажений, т. е. где Х — принятое в геодезии обозначение длины дуги осевого меридиана от экватора до текущей параллели. Подставив значение характеристики в уравнения (199), получим для проекций с симметричной картографической сеткой
но но откуда так как то где обозначим После замены получим где Подставим производные в уравнения (198): При составлении карт масштаба мельче 1: 50 000 члены формул, содержащие В практике прямоугольные координаты проекции Гаусса— Крюгера обычно определяют по «Таблицам координат Гаусса— Крюгера и таблицам размеров рамок и площадей трапеций топографических съемок» (М., Госгеолтехиздат, 1963) и по «Таблицам прямоугольных координат углов рамок, размеров и площадей трапеций топографических съемок масштаба 1: 5 000» (М., Геодезиздат, 1953). Рассмотренная проекция Гаусса—Крюгера не является строго равноугольной, так как при ее получении использовано разложение в такой ряд, для которого выполняется только одно из условий Коши—Римана Выведем формулу частного масштаба длин, ограничивая ее членами, содержащими Для нахождения частного масштаба длин воспользуемся известной формулой
а также значениями производных Подставим полученное значение g в формулу масштаба ( В картографической практике величину Исследования показали, что изоколы в проекции Гаусса—Крюгера имеют вид овалов, вытянутых вдоль осевого меридиана. Максимальные искажения длин в каждой зоне будут при
В ряде стран применяют сейчас для топографических карт так называемую универсальную поперечно-цилиндрическую проекцию Меркатора (UTM) в шестиградусных зонах. Эта проекция очень близка по своим свойствам и распределению искажений к проекции Гаусса—Крюгера, но в ней на осевом меридиане каждой зоны масштаб На расстоянии около 200 км по обе стороны от осевого меридиана и параллельно ему находятся две изоколы с нулевым искажением длин. При дальнейшем удалении от осевого меридиана масштаб длин становится больше единицы и достигает максимума на пересечении крайних меридианов зоны с экватором (
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.49.13 (0.012 с.) |

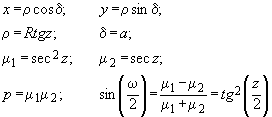
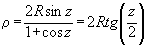 .
.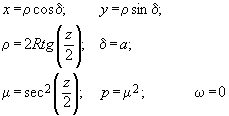
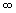 ), т. е. проектирование ведется пучком параллельных лучей.
), т. е. проектирование ведется пучком параллельных лучей.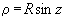 .
.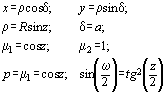
 ортографическая проекция является равнопромежуточной по альмукантаратам (нормальная — по параллелям).
ортографическая проекция является равнопромежуточной по альмукантаратам (нормальная — по параллелям).
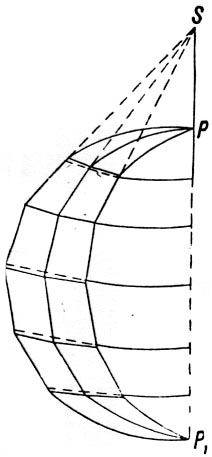


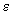 , возникающего при соединении четырех трапеций, имеющих общую вершину, определяется по формуле -
, возникающего при соединении четырех трапеций, имеющих общую вершину, определяется по формуле - 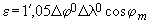 (7.18)
(7.18)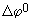 и
и  —соответственно разности широт крайних параллелей и долгот крайних меридианов трапеции, выраженные в градусах,
—соответственно разности широт крайних параллелей и долгот крайних меридианов трапеции, выраженные в градусах,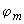 —широта общей вершины четырех трапеций,
—широта общей вершины четырех трапеций,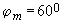 угловой разрыв для трапеций масштаба 1:1000000, с размерами сторон
угловой разрыв для трапеций масштаба 1:1000000, с размерами сторон
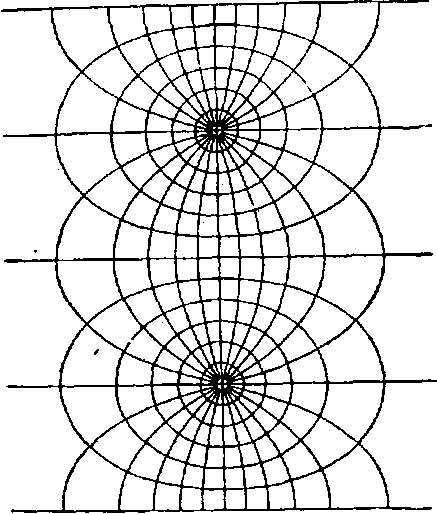

 — изометрические координаты, а функция F может быть получена разными способами; она может быть линейной, показательной, степенной, функция может быть получена и путем разложения в ряд Тейлора.
— изометрические координаты, а функция F может быть получена разными способами; она может быть линейной, показательной, степенной, функция может быть получена и путем разложения в ряд Тейлора. 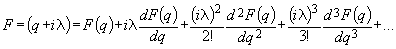 (198)
(198) и т.д. поэтому из формулы (198) получим
и т.д. поэтому из формулы (198) получим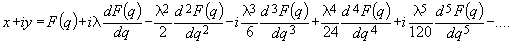
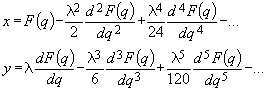 (199)
(199) .
.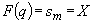
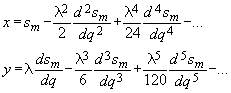 (200)
(200)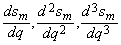 и т. д. и подставим
и т. д. и подставим

 из формул (197) и
из формул (197) и 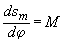 , поэтому
, поэтому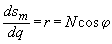 , т. е. первая производная равна радиусу текущей параллели;
, т. е. первая производная равна радиусу текущей параллели;
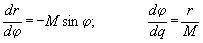
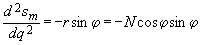
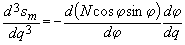

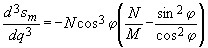
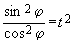
 на
на 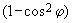 в формуле
в формуле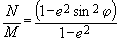
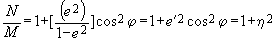
 — квадрат второго эксцентриситета; тогда
— квадрат второго эксцентриситета; тогда Четвертую и пятую производные напишем без вывода
Четвертую и пятую производные напишем без вывода
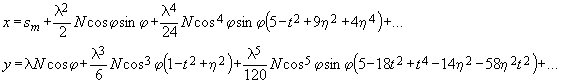
 и
и 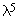 , обычно не учитывают.
, обычно не учитывают. .
.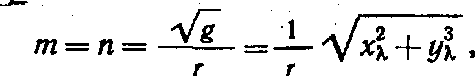
 . Тогда коэффициент Гаусса g равен
. Тогда коэффициент Гаусса g равен
 в градусах):
в градусах):
 обычно не учитывают. Поэтому
обычно не учитывают. Поэтому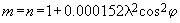 (201)
(201)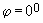 и
и 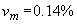 .
.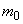 равен 0,9996, а не единице.
равен 0,9996, а не единице.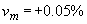 ).
).


