Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямоугольная диметрическая проекцияСодержание книги
Поиск на нашем сайте
Расположение осей координат в прямоугольной диметрической проекции показаны на рис 11.6. На практике коэффициенты искажения по осям x и z принимают равным единице, по оси y – 0,5. Таким образом, при построении диметрии вдоль координатных осей x и z откладывают натуральные размеры предмета, а вдоль оси y – в два раза меньше, например, на рис. 11.6 – куб.
Окружности в прямоугольной диметрической проекции показаны на рис. 11.7. В прямоугольной диметрии так же, как в прямоугольной изометрии, большие оси эллипсов всегда располагаются перпендикулярно отсутствующей в данной плоскости аксонометрической оси, а малые оси - параллельны ей.
КОСОУГОЛЬНАЯ ФРОНТАЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
Расположение осей координат в косоугольной фронтальной диметрической проекции показаны на рис 11.10. На практике коэффициенты искажения по осям x и z принимают равным единице, по оси y – 0,5 (на рис. 11.10 – куб). Окружности в прямоугольной диметрической проекции показаны на рис. 11.11. Одна из них, расположенная в плоскостиV, проецируется без искажения, две другие - в виде эллипсов (строятся так же, как в прямоуголбной диметрии).
Таким образом, косоугольная фронтальная диметрическая проекция предпочтительна в тех случаях, когда окружности лежат в плоскостях, параллельных плоскости V. Пример изображения детали с отверстиями в косоугольной фронтальной диметрии показан на рис.11.12.
Рисунок11.12
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Для чего используются аксонометрические проекции? 2. Какими свойствами обладают аксонометрические проекции? 3. Какие аксонометрические проекции вы знаете? 4. Как расположены оси координат в прямоугольной изометрической проекции? 5. Какие коэффициенты искажения по осям в прямоугольной изометрической проекции? 6. Как вычерчиваются окружности в аксонометрических проекциях? 7. Как располагаются оси эллипсов в прямоугольной изометрической проекции? 8. Как строят эллипс в прямоугольной изометрической проекции? 9. Как расположены оси координат в прямоугольной диметрической проекции? 10. Какие коэффициенты искажения по осям в прямоугольной диметрической проекции? 11. Как располагаются оси эллипсов в прямоугольной диметрической проекции? 12. Как строят эллипсы в прямоугольной диметрической проекции? 13. Как расположены оси координат в косоугольной фронтальной диметрической проекции? 14. Какие коэффициенты искажения по осям в косоугольной фронтальной диметрической проекции? 15. Как располагаются оси эллипсов в косоугольной фронтальной диметрической проекции? 16. Как строят эллипс в косоугольной фронтальной диметрической проекции? 17. В каких случаях косоугольнаяфронтальная диметрическая проекция предпочтительна? 18. Выберите оси и изображение куба, соответствующие косоугольной фронтальной диметрической проекции. (Ответ:,)
19. Установить соответствие вида аксонометрической проекции и чертежа детали. (Ответ:1-, 2-,3-)
20. В какой аксонометрической проекции изображена деталь?
- в прямоугольной изометрии - в прямоугольной диметрии - в косоугольной фронтальной диметрии
21. В какой аксонометрической проекции изображена деталь?
- в прямоугольной изометрии - в косоугольной фронтальной диметрии
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 2068; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.136 (0.006 с.) |



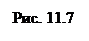

 Рисунок 11.8
Рисунок 11.8
 Рисунок11.9
Рисунок11.9

 Рисунок 11.10
Рисунок 11.10

 Рисунок 11.11
Рисунок 11.11