
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перпендикулярной плоскости проекцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сущность метода: плоскости проекций остаются неподвижными, а геометрический объект меняет свое положение. При вращении каждая точка геометрической фигуры перемещается в плоскости, перпендикулярной к оси вращения. Траектория движения точек представляет собой окружность. Решение четырех основных задач методом вращения вокруг оси, перпендикулярной плоскости проекций:
Задача 1.
Для того, чтобы отрезок АВ занял положение уровня, переместим А по окружности так, чтобы В″А1″ ║ х. Положение А1′ будет находится на пересечении линии связи, проведенной от А1″ и горизонтальной прямой от А′ (проекции окружности). Таким образом, отрезок АВ занял положение горизонтали (А1″В″ - натуральная величина АВ, угол между А1′В′ и х является действительной величиной угла наклона АВ к плоскости V).
Задача 2.
Таким образом, отрезок АВ занял фронтально-проецирующее положение.
Задача 3. На рис. 6.8 задана плоскость общего положения АВС. Для того чтобы она заняла проецирующее положение, зададим какую-либо линию уровня плоскости, например горизонталь плоскости h. Пусть ось вращения i1 ^ Н и проходит через точку С. Переведем h во фронтально-проецирующее положение путем вращения вокруг оси i1. При этом она повернется на угол φ. На такой же угол вращают остальные точки плоскости А, В, С. Таким образом, получим фронтально-проецируюшую плоскость А1В1С (угол между В1″С″А1″ и х является действительной величиной угла наклона АВС к плоскости Н).
Задача 4. На рис. 6.9 задана плоскость общего положения АВС. Для того чтобы она заняла положение плоскости уровня, ее сначала нужно перевести в проецирующее положение. Выполнив для этого необходимые действия (см. задачу 3), введем еще одну ось вращения i2 ^ V, которая проходит через точку В. Провращаем плоскость А1В1С так, чтобы А2″В1″С2″ ║ x. Таким образом, плоскость займет положение горизонтальной плоскости (А2′В1′С2′ - натуральная величина АВС).
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какие способы преобразования чертежа вы знаете? Их сущность. 2. Сколько и в какой последовательности нужно ввести дополнительных плоскостей для преобразования прямой общего положения в проецирующее? 3. Каким образом нужно выбрать ось вращения при применении способа вращения вокруг оси, перпендикулярной к плоскости проекций, для упрощения построений? 4. Какие построения необходимо выполнить, чтобы плоскость общего положения преобразовать в проецирующее, используя способ вращения вокруг оси, перпендикулярной к плоскости проекций? 5. Как определить натуральную величину отрезка и углы его наклона к плоскостям проекций с помощью способов преобразования чертежа? 6. В какой плоскости перемещается точка при вращении ее вокруг оси, перпендикулярной фронтальной плоскости проекции? - в плоскости, параллельной V - в плоскости, параллельной H - в плоскости, параллельной W
7. В какой плоскости происходит вращение точек отрезка АВ?
- в плоскости, параллельной V - в плоскости, параллельной H - в плоскости, параллельной W
8. Какая проекция отрезка АВ является его натуральной величиной?
- А″В″ - А′В′ - А1″В1″ - А1′В1′
- метод перемены плоскостей - метод прямоугольного треугольника - метод вращения
10. Какая проекция треугольника АВС является его натуральной величиной?
- А″В″С″ - А′В′С′ - А1″В1″С1″ - А1′В1′С1′ 11. Для того, чтобы перевести треугольник АВС в проецирующее положение ось х1 задают…
- параллельно В′С′ - перпендикулярно А′H′ - перпендикулярно А″H″ - произвольно
ЗАНЯТИЕ 6 КРИВЫЕ ЛИНИИ Кривую линию можно представить как траекторию точки, перемещающейся в пространстве или на плоскости, Кривые линии могут быть плоские, т.е. такие, все точки которых принадлежат одной плоскости и пространственные, точки которых не принадлежат одной плоскости. Примерами плоских кривых являются: окружность, эллипс, парабола. Примером пространственной кривой является винтовая линия.
ПОВЕРХНОСТИ ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Поверхность - это совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Линию, перемещающуюся в пространстве и образующую поверхность, называют образующей. Образующие могут быть прямыми и кривыми линиями. Одна и та же поверхность может быть образована различными способами – движениями различных образующих. Например, прямой круговой цилиндр (рис 8.1) может быть образован: - вращением прямой образующей вокруг неподвижной оси, ей параллельной; - движением образующей окружности, центр которой перемешается по прямой, перпендикулярной плоскости окружности; - прямолинейным движением сферы. Из всех способов образования поверхностей необходимо выбирать такие, которые являются наиболее простыми и удобными для решения задач. Рассмотрим краткую классификацию поверхностей. Линейчатая поверхность — поверхность, которая может быть образована прямой линией. Например: цилиндр, конус (рис. 8.1). Нелинейчатая поверхность — поверхность, которая образована кривой линией. Например: сфера, тор (рис. 8.1).
Развертываемая поверхность — это линейчатая поверхность, которая может быть развернута так, что всеми своими точками она совместится с плоскостью без каких-либо повреждений поверхности (разрывов и складок). Например: цилиндр, конус. Неразвертываемые поверхности - это нелинейчатые поверхности и те линейчатые, которые не могут быть развернуты в плоскость. Например: сфера.
Поверхность вращения - поверхность, образованная при вращении некоторой образующей линии вокруг неподвижной оси. Например: цилиндр, конус, сфера, тор (рис. 8.1). В инженерной практике большое распространение получили винтовая и циклическая поверхности. Винтовая поверхность - поверхность, образованная винтовым движением некоторой линии (рис. 8.2). Используется для создания деталей машин, например – шнеки. Циклическая поверхность - поверхность, образованная с помощью окружности, центр которой перемещается по криволинейной направляющей (рис. 8.2). Используется для создания переходных участков между трубопроводами.
Гранные поверхности (многогранники) – призмы и пирамиды (рис. 8.3).
Проецирующая поверхность - это поверхность, образующие или ребра которой перпендикулярны какой - либо плоскости проекций. Например: прямой круговой цилиндр, четырехгранная призма.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.31.48 (0.01 с.) |

 На рис. 6.6 задан отрезок общего положения АВ. Обозначим i1 - ось вращения. Пусть i1 ^ V и проходит через точку В. Тогда при вращении вокруг оси В останется на месте, А будет перемещаться в плоскости, перпендикулярной i1, а следовательно параллельной V. Таким образом, окружность, по которой движется точка, на плоскость V проецируется без искажения, а на плоскость Н – в отрезок, параллельный оси х.
На рис. 6.6 задан отрезок общего положения АВ. Обозначим i1 - ось вращения. Пусть i1 ^ V и проходит через точку В. Тогда при вращении вокруг оси В останется на месте, А будет перемещаться в плоскости, перпендикулярной i1, а следовательно параллельной V. Таким образом, окружность, по которой движется точка, на плоскость V проецируется без искажения, а на плоскость Н – в отрезок, параллельный оси х. На рис. 6.7 задан отрезок общего положения АВ. Для того, чтобы АВ занял проецирующее положение, его сначала нужно перевести в положение уровня. Выполнив для этого необходимые действия (см. задачу 1), введем еще одну ось вращения i2 ^ Н. Переместим А1′ и В′ по окружности так, чтобы А2′ В2′ ^ х. Положение А2″ и В2″ будет находится на пересечении линии связи, проведенной от А2′ В2′ и горизонтальной прямой от В″А1″ (проекции окружности, по которой двигались А1′ и В′).
На рис. 6.7 задан отрезок общего положения АВ. Для того, чтобы АВ занял проецирующее положение, его сначала нужно перевести в положение уровня. Выполнив для этого необходимые действия (см. задачу 1), введем еще одну ось вращения i2 ^ Н. Переместим А1′ и В′ по окружности так, чтобы А2′ В2′ ^ х. Положение А2″ и В2″ будет находится на пересечении линии связи, проведенной от А2′ В2′ и горизонтальной прямой от В″А1″ (проекции окружности, по которой двигались А1′ и В′).



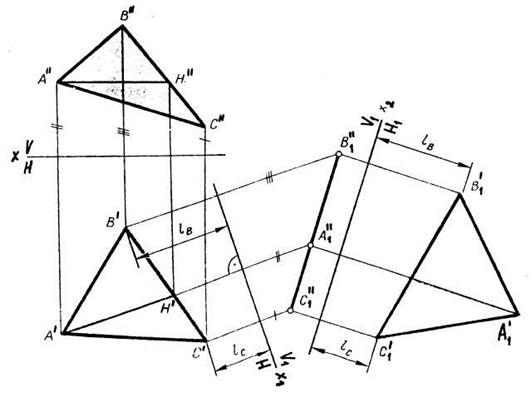 9. Какой метод использован для определения натуральной величины треугольника АВС?
9. Какой метод использован для определения натуральной величины треугольника АВС?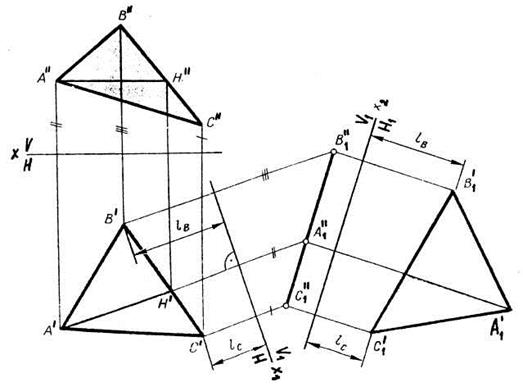

 Для построения ортогональных проекций кривой (пространственной или плоской) необходимо построить проекции ряда точек, принадлежащих этой кривой, и соединить их между собой в той же последовательности, в какой они располагались на оригинале (рис.7.1.).
Для построения ортогональных проекций кривой (пространственной или плоской) необходимо построить проекции ряда точек, принадлежащих этой кривой, и соединить их между собой в той же последовательности, в какой они располагались на оригинале (рис.7.1.).










