
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональные проекции точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Точка относится к основным, неопределяемым понятиям геометрии, она не имеет размеров.
На рис. 2.1 показан I октант пространственной модели координатных плоскостей проекций. Положение точки в пространстве определяется координатами (х, у, z), показывающими величины расстояний, на которые точка удалена от плоскостей проекций. Чтобы определить эти расстояния, достаточно через точку А провести прямые, перпендикулярные к плоскостям проекций, определить точки встречи этих прямых с плоскостями проекций А ', А ", А '" и измерить величины отрезков [ АА '], [ АА "], [ АА '"], которые укажут соответственно значения аппликаты z, ординаты у и абсциссы х точки А. Точки А ', А ", А '" называют ортогональными проекциями точки А, при этом согласно принятым обозначениям: А ' – горизонтальная проекция точки А; А " – фронтальная проекция точки А; А '" – профильная проекция точки А. Эпюр точки А показан на рис. 2.2. Отметим, что А ' определяется координатами (х, у), А " (х, z), А '" (у, z). А ' и А " находятся на одной вертикальной линии связи, А " и А '" – на одной горизонтальной линии связи. Таким образом, точка А находится в I октанте и имеет координаты (40, 30, 50). Она удалена от горизонтальной плоскости проекций на 50 мм, от фронтальной плоскости проекций - на 30 мм, от профильной плоскости проекций - на 40 мм. На рис. 2.3 и 2.4 изображена точка В с координатами (40, 0, 30). Точка В
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Перечислите основные методы проецирования, их сущность. 2. Как изображают пространственную модель координатных плоскостей? 3. Что называют эпюром? 4. Каким образом пространственную модель координатных плоскостей, состоящую из трех взаимно перпендикулярных плоскостей, преобразуют в эпюр? 5. Как обозначают проекции точки на плоскости проекций Н (П1), V (П2), W (П3)? 6. Какие координаты определяют проекции точки на плоскости Н, V, W? 7. Как построить недостающую проекцию точки по двум данным проекциям? 8. Какие координаты определяют расстояние от точки до плоскостей Н, V, W? 9. Точка А (0,30,0) принадлежит … - только горизонтальной плоскости проекции - оси x - оси y - оси z - только профильной плоскости проекций
10. Точка А (0,0,30) принадлежит … - только горизонтальной плоскости проекции - оси x - оси y - оси z - только профильной плоскости проекций 11. Точка С (0,30,40) принадлежит … - только горизонтальной плоскости проекции - только профильной плоскости проекции - только фронтальной плоскости проекции - оси х - оси y
12. Точка К принадлежит …
- только фронтальной плоскости проекции -только профильной плоскости проекции - оси y - оси z
13. Точка N принадлежит …
- только фронтальной плоскости проекции - только профильной плоскости проекции - оси y - оси z
14. Точка М принадлежит …
- оси z - только горизонтальной плоскости проекции - только фронтальной плоскости проекции - только профильной плоскости проекции
15. Точка М принадлежит …
- только горизонтальной плоскости проекции - только фронтальной плоскости проекции - только профильной плоскости проекции - оси х - оси z
16. Точка N принадлежит …
- только фронтальной плоскости проекции - только профильной плоскости проекции - оси х - оси z 17. Выше всех расположена точка …
- А - В - С - Д - Е
18. Дальше всех от плоскости V расположена точка…
- А - В - С - Д - Е
ЗАНЯТИЕ 2 3. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПРЯМОЙ
При ортогональном проецировании на плоскость прямая проецируется в прямую. Поэтому, для определения проекции прямой достаточно знать проекции двух точек, принадлежащих этой прямой.
ПРЯМЫЕ ОБЩЕГО ПОЛОЖЕНИЯ Прямая общего положения - это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций (рис. 3.1, 3.2).
ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ. Прямая частного положения - это прямая параллельная или перпендикулярная одной из плоскостей проекций.
Прямые уровня
Прямая, параллельная горизонтальной плоскости проекций, называется горизонталью h (рис. 3.3). Все точки горизонтали удалены на одинаковое расстояние от плоскости П1.
Прямая, параллельная фронтальной плоскости проекций, называется фронталью f (рис. 3.4 ). Все точки фронталиудалены на одинаковое расстояние от плоскости П2.
Прямая, параллельная профильной плоскости проекций, называется профильной прямой w (рис. 3.5). Все точки профильной прямой удалены на одинаковое расстояние от плоскости П3. Проецирующие прямые Проецирующая прямая - прямая, перпендикулярная какой-либо плоскости проекций и параллельная двум другим.
Прямая, перпендикулярная горизонтальной плоскости проекций и параллельная двум другим называется горизонтально-проецирующей (рис. 3.6). Такая прямая проецируется на плоскость П1 в точку.
Прямая, перпендикулярная фронтальной плоскости проекций и параллельная двум другим называется фронтально-проецирующей (рис. 3.7). Такая прямая проецируется на плоскость П2 в точку.
Прямая, перпендикулярная профильной плоскости проекций и параллельная двум другим называется профильно-проецирующей (рис. 3.8). Такая прямая проецируется на плоскость П3 в точку.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.172.11 (0.007 с.) |


 V, удалена от горизонтальной плоскости проекций на 30 мм, от профильной плоскости проекций - на 40 мм
V, удалена от горизонтальной плоскости проекций на 30 мм, от профильной плоскости проекций - на 40 мм
 - только горизонтальной плоскости проекции
- только горизонтальной плоскости проекции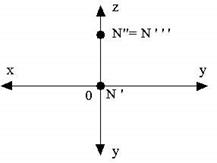 - только горизонтальной плоскости проекции
- только горизонтальной плоскости проекции - оси х
- оси х
 - только горизонтальной плоскости проекции
- только горизонтальной плоскости проекции


 Прямая уровня – это прямая, параллельная одной из плоскостей проекций.
Прямая уровня – это прямая, параллельная одной из плоскостей проекций.







