Проецирование прямого угла на плоскость проекций

Теорема о частном проецировании прямого угла

Если плоскость прямого угла не перпендикулярна и не параллельна плоскости проекций и хотя бы одна сторона его параллельна этой плоскости, то прямой угол проецируется на нее без искажения.

Пусть угол АВС – прямой (рис. 65) и сторона ВС || Н, следовательно, проекция bc || BC. Сторону АВ продолжим до пересечения с плоскостью Н и через точку К проводим прямую KN || bc. Следовательно, KN || BC.

Отсюда следует, что угол BKN – прямой. Согласно теореме о трех перпендикулярах, угол bKN – прямой, следовательно, угол Kbc = 90°.

 

 

Рис. 65. Пространственная модель проецирования прямого угла

Примечание. Этой теореме о проецировании прямого угла соответствуют две обратные теоремы (доказательства не приводятся).

1. Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь при условии, что по крайней мере одна из сторон этого угла параллельна плоскости проекций.

2. Если проекция некоторого угла, у которого одна сторона параллельна плоскости проекций, представляет прямой угол, то проецируемый угол также прямой.

На основании этих теорем можно установить, что углы, изображенные на рис. 66, в пространстве – прямые.

 

б

а

 

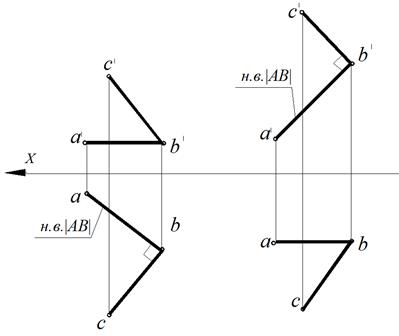
Рис. 66. Проецирование прямого угла на эпюре Монжа:

а – одна из сторон угла – горизонталь; б – одна из сторон угла – фронталь

 

Рассмотрим угол В (рис. 66 а).

В пространстве угол В прямой, т. к. на эпюре видно, что прямая АВ является горизонталью (h′ || X) и ∠ a = 90° (согласно первой обратной теореме).

Рассмотрим угол В (рис. 66 б).

В пространстве угол В прямой, т. к. одна его сторона является фронталью (АВ || V; ab || X) и фронтальная проекция ∠ b ′ = 90°.

Из этой теоремы следует простой вывод – к прямой можно провести перпендикуляр там, где прямая проецируется в натуральную величину.

При решении позиционных и метрических задач начертательной геометрии, опираясь на эти теоремы, можно строить две взаимно перпендикулярные прямые, что, в конечном итоге, позволяет определять расстояния, строить взаимно перпендикулярные плоскости.

Рассмотрим несколько задач по теме данного материала.

Задача 1. Через точку А провести прямую, перпендикулярную прямой М (рис. 67).

Анализируя графическое условие задачи, отмечаем, что m || X, а это значит, что прямая М является фронталью (М || V).

Следовательно, построение искомой прямой надо начинать с фронтальной проекции, проводя ее перпендикулярно проекции m ׳, т. к. на фронтальной плоскости проекций прямая М проецируется без искажения и на фронтальную плоскость проекций V прямой угол между данной и вновь построенной прямыми будет проецироваться без искажения.

Порядок выполнения графической части задачи:

1. Строим фронтальную проекцию искомого отрезка a′b′ ⊥ m ′.

2. Определяем положение точки b ׳ на проекции m ׳ и по проекционной связи определяем горизонтальную проекцию b на проекции m.

3. Строим горизонтальную проекцию искомого отрезка ab.

 

 

Рис. 67. Построение перпендикуляра к прямой М Рис. 68. Построение высоты в ∆ АВС

 

Задача 2. Через вершину С провести высоту треугольника АВС (рис. 68).

Решение. Анализируем эпюр и отмечаем, что сторона треугольника АВ || H, при этом ее горизонтальная проекция отображается в натуральную величину.

Следовательно, построение высоты надо начинать с горизонтальной проекции.

Порядок выполнения графической части задачи:

1. Из точки с проводим отрезок перпендикулярно стороне ab.

2. Точка d –основание высоты, cd – горизонтальная проекция высоты.

3. Проецируем точку d на фронтальную проекцию стороны a′b′ и получаем фронтальную проекцию точки d′ и строим фронтальную проекцию высоты c′d′.

 

Задача 3. Определить расстояние от точки К до прямой N (рис. 69).

Решение. Следует отметить, что при решении задач на определение расстояний, необходимо строить не только проекции расстояния, но определять его натуральную величину.

Кратчайшим расстоянием от точки до прямой является величина перпендикуляра, опущенного из этой точки на прямую. Анализируя эпюр, отмечаем, что прямая N является фронталью и отображается на фронтальной проекции без искажения.

Следовательно, построение проекции перпендикуляра необходимо начинать с его фронтальной проекции.

Порядок выполнения графической части задачи:

1. Из точки k ′ опускаем перпендикуляр на проекцию прямой n′, получаем точку e′. Фронтальная проекция перпендикуляра – k ′ e ′.

2. Проецируем полученную точку на горизонтальную проекцию прямой n, получаем точку e и горизонтальную проекцию перпендикуляра ke.

3. Судя по проекциям, прямая КЕ общего положения. Методом прямоугольного треугольника определяем ее натуральную величину | KE|.

Расстояние от точки К до прямой N равно длине отрезка – К _о е′.

KE, N = K _o e′ = 30 мм.

3.5. Особые линии плоскости

Прямые, занимающим особое положение в плоскости:

1. Линии уровня плоскости.

2. Линии наибольшего наклона плоскости к плоскостям проекций.

 

Линии уровня плоскости

 

Линии уровня плоскости – прямые, лежащие в заданной плоскости и параллельные плоскостям проекций: горизонтали, фронтали, профильные прямые.

Горизонталь плоскости – прямая, лежащая в заданной плоскости и параллельная плоскости проекций Н. Следует запомнить, что все горизонтали одной и той же плоскости параллельны между собой.

Горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости, горизонтальный след плоскости является нулевой горизонталью плоскости. Чтобы построить горизонталь в плоскости Р,заданной следами, надо на фронтальной проекции Р_V отметить точку d' – фронтальную проекцию следа горизонтали (рис. 67 а). Через нее проводим фронтальную проекцию горизонтали параллельно оси х. На оси х находим горизонтальную проекцию d. Прямая, проведенная из точки d параллельно следу Р_Н плоскости, представляет горизонтальную проекцию горизонтали.

На рис. 70 б проекции горизонтали проведены через проекции точки D и точки 1 прямой ЕС плоскости, заданной треугольником СDE. Построение горизонтали всегда начинают с фронтальной проекции d'1', которая параллельна оси Х. По свойству принадлежности находят горизонтальную проекцию точки 1 и проводят горизонтальную проекцию горизонтали.

 

а

б

 

Рис. 70. Горизонталь плоскости:

а – в плоскости Р, заданной следами; б – в плоскости, заданной ∆ СDE

 

Фронталь плоскости – прямая, лежащая в плоскости и параллельная плоскости проекций V (рис. 71).

Построение фронтали и профильных прямых выполняется аналогично построению горизонтали, опираясь на известные свойства проекций линий уровня и свойство принадлежности, и начинают его с той проекции, которая параллельна соответствующей проекционной оси.Все фронтали одной и той же плоскости параллельны между собой. То же самое можно сказать и о профильных прямых уровня плоскости.

Профильная прямая уровня плоскости – это прямая, лежащая в данной плоскости и параллельная профильной плоскости проекций (рис. 72).

б

а

Рис. 71. Фронталь плоскости:

а – в плоскости Р, заданной следами; б – в плоскости, заданной ∆ СDE

 

Рис. 72. Профильная прямая уровня ВЕ плоскости ∆ АВС