Построение точки по координатам

 

Плоскости проекций V, H, W принимаются за координатные плоскости, а оси проекций X, Y, Z за координатные оси как положительные, так и отрицательные (рис. 10).

Положение точки в пространстве задается тремя координатами – X, Y, Z. Проекции точки задаются двумя координатами: а (х, y), а′ (х, z), а′′ (y, z).

Зная направление для положительного и отрицательного значений координатных осей, принимая во внимание свойства проекций точки, можно построить проекции точки по координатам. Рассмотрим несколько задач на эту тему.

 

Задача. Построить проекции точки А (–10; 40; –30) (рис. 10).

 

 

Рис. 10. Построение проекций точки А по координатам

Для построения фронтальной проекции а′ точки А справа от точки О на оси Х откладываем значение Х = –10. Вниз от точки О по направлению оси Z откладываем значение Z = –30. Пересечением перпендикуляров из точек а_X и а_Z,восстановленных к соответствующим осям Х и Z, определяем точку а′.

Для построения горизонтальной проекции а точки А по направлению оси Y вниз от точки О откладываем значение y = – 40. Через точку а_Y проводим перпендикуляр до пересечения с линией связи а′а_X. Отмечаем точку а – горизонтальную проекцию точки А. По расположению фронтальной и горизонтальной проекций точки А определяем, что точка А расположена в VΙΙΙ октанте.

Для построения профильной проекции а′′ точки А через ее фронтальную проекцию а′ проводим линию связи а′а_Z и на ней, вправо от точки а_Z, откладываем значение y = 40. Отмечаем точку а′′ – профильную проекцию точки А.

 

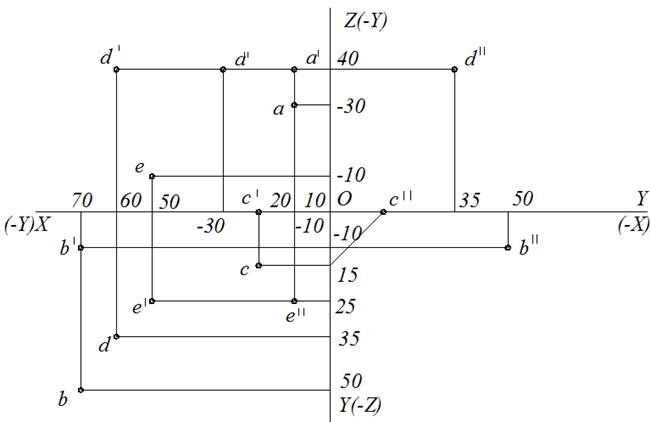
Задача. Построить проекции точек по координатам и указать октант, в котором находится каждая из них.

Исходные данные: А (10; –30; 40), В (70; 50; –10), С (20; 15; 0), D (60; 35; 40), Е (50; –10; –25).

Решение. Порядок выполнения графической части задачи (рис. 11):

1. Проводим оси координат Х, Y, Z. Указываем положительные и отрицательные их направления.

2. Построение точек выполняем в масштабе 1:1.

Точка А (10; –30; 40):

Фронтальную проекцию а′ точки А определяем по координатам Х, Z; по оси Х откладываем 10 мм, по оси Z – 40 мм.

Горизонтальную проекцию а точки А определяем по координатам Х,(– Y), расстояние 30 мм откладываем по оси (– Y), совпадающей с положительным направлением оси Z.

Профильную проекцию а′′ точки А определяем по координатам (– Y), Z. В этом случае расстояние 30 мм откладывается по оси (– Y), совпадающей с положительным направлением оси Х. Следовательно, точка А находится во ΙΙ октанте.

Точка В (70; 50; –10):

Строим фронтальную проекцию b′ (Х = 70; Y = –10) точки А. Расстояние 10 мм нужно отложить на отрицательном направлении оси Z. Уточните: фронтальная b′ и горизонтальная b проекции точки В будут расположены на линии связи ниже оси Х. Профильная проекция b′′ точки В располагается справа от оси Z и ниже оси Х. Анализируя знаки координат (+ + –) и расположение проекций точки, делаем вывод – точка В находится в ΙV октанте.

Точка С (20; 15; 0):

При построении этой точки очевидно, что фронтальная проекция с′ точки С лежит на оси Х, а ее профильная проекция а′′ лежит на оси Y, совпадающей с отрицательным направлением оси Х. Удаление точки С от плоскости проекций Н равно нулю (y = 0), следовательно, точка С лежит в плоскости Н, на границе Ι и ΙV октантов.

Точка D (60; 35; 40):

Все значения координат положительные, следовательно, точка D находится в Ι октанте.

Точка Е (50; –10; –25):

При отрицательных значениях Y и Z точка располагается в ΙΙΙ октанте. Проекции такой точки располагаются:

- фронтальная проекция е′ точки Е располагается ниже оси Х, слева от оси Y;

- горизонтальная проекция е точки Е располагается выше оси Х, слева от оси Z;

- профильная проекция е′′ точки Е располагается слева от оси Z, ниже оси Х.

Вывод. Положение точки в пространстве вполне определено, если известны три ее координаты или две любые ортогональные проекции. Как следствие из этого – по двум любым заданным ортогональным проекциям точки можно всегда построить недостающую ее третью ортогональную проекцию.

 

Рис. 11. Построение точек по координатам с указанием октантов

Рассмотри построение точки по двум заданным ортогональным проекциям.

Задача. По двум заданным ортогональным проекциям построить недостающую проекцию точки В (рис. 12).

 

Рис. 12. Графическое условие задачи

Решение. Анализируем графическое условие задачи: заданы фронтальная и профильная проекции точки В. Это значит, заданы все три координаты точки В. Следовательно, необходимо построить ее горизонтальную проекцию.

Порядок выполнения графической части задачи:

1. Для построения горизонтальной проекции точки В необходимо знать Х_В и У_В. Эти координаты находим на чертеже.

2. Замеряем У_В = b_Z b′′ и откладываем эту координату вдоль линии связи от оси ОХ от точки b_Х.

3. Строим горизонтальную проекцию точки В (рис. 13).

 

 

Рис. 13. Построение недостающей проекции точки В

ПРЯМАЯ ЛИНИЯ

При ортогональном проецировании на плоскости проекций прямая линия проецируется в виде прямой. Чтобы построить проекции этой прямой линии, проходящей через заданные точки А и В, нужно построить проекции этих точек и провести прямые линии через их одноименные проекции (рис. 14). Получим:

аb – горизонтальную проекцию отрезка прямой;

а′b′ – фронтальную проекцию отрезка прямой.

 

Рис. 14. Проекции отрезка прямой, проходящего через две точки

 

 

Следы прямой

Прямая пересекает плоскости проекций в точках, которые называются следами прямой.

Точка пересечения прямой N с горизонтальной плоскостью проекций Н (П₁) называется горизонтальным следом N_H.

Точка пересечения прямой с фронтальной плоскостью проекций V (П₂) – фронтальным следом N_V.

Точка пересечения прямой N с профильной плоскостью проекций W (П₃) – профильным следом N_W прямой.

Вывод:

· горизонтальный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая в горизонтальной плоскости проекций H (П₁);

· фронтальный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая во фронтальной плоскости проекций V (П₂);

· профильный след прямой – это точка, принадлежащая одновременно данной прямой и лежащая в профильной плоскости проекций W (П₃).

 

Задача. Построить точки пересечения прямой N с горизонтальной Н (П₁) и фронтальной V (П₂) плоскостями проекций (рис. 15 аб).

Анализируя задачу, приходим к выводу, что необходимо построить горизонтальный и фронтальный следы прямой.

Решение

1. Построение фронтального следа N_V.

Необходимо построить точку, принадлежащую прямой N и фронтальной плоскости проекций. Согласно изложенному ранее материалу, горизонтальная проекция искомой точки должна:

– лежать на оси Х;

– принадлежать горизонтальной проекции прямой N.

Порядок выполнения графической части задачи:

1.1. Отмечаем точку пересечения горизонтальной проекции n прямой N с осью Х, получаем точку n_V – горизонтальную проекцию фронтального следа.

1.2. Через точку n_V проводим линию связи перпендикулярно оси Х.

1.3. Находим точку пересечения линии связи с фронтальной проекцией n′ прямой N, получаем точку N_V – фронтальную проекцию фронтального следа. Через эту точку прямая уходит во вторую четверть (рис. 15 а) и в третью четверть (рис. 15 б).

2. Построение горизонтального следа N_H.

Необходимо построить точку, принадлежащую прямой N и горизонтальной плоскости проекций Н. Согласно изложенному ранее материалу, фронтальная проекция искомой точки должна:

– лежать на оси Х;

– принадлежать фронтальной проекции прямой N.

Порядок выполнения графической части задачи:

2.1. Отмечаем точку пересечения фронтальной проекции n ′ прямой N с осью Х, получаем точку n_H – фронтальную проекцию горизонтального следа.

2.2. Через точку n_H проводим линию связи перпендикулярно оси Х.

2.3. Находим точку пересечения линии связи с горизонтальной проекцией n прямой N, получаем фронтальную проекцию фронтального следа. В этой точке прямая пересекает горизонтальную плоскость и уходит в четвертую четверть (рис. 15 а, б).

 

а

б

 

Рис. 15. Построение следов прямой линии N:

а – прямая уходит во вторую четверть; б – прямая уходит в третью четверть