Комплексный чертеж и наглядное изображение точки в I–IV октантах

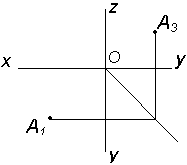
Рассмотрим пример построения точек А, В, С, D в различных октантах (табл. 2.4).

Таблица 2.4

Октант	Наглядное изображение	Комплексный чертеж
I
II
III
IV

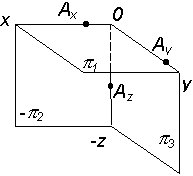
Пример построения третьей проекции точки по двум заданным

Точка в пространстве определяется любыми двумя своими проекциями. При необходимости построения третьей проекции по двум заданным необходимо воспользоваться соответствием отрезков линий проекционной связи, полученных при определении расстояний от точки до плоскости проекций (см. рис. 2.27 и рис. 2.28).

Примеры решения задач в I октанте

Дано А1; А2	Построить А3
Дано А2; А3	Построить А1
Дано А1; А3	Построить А2

Рассмотрим алгоритм построения точки А (табл. 2.5)

Таблица 2.5

Алгоритм построения точки А
по заданным координатам А (x = 5, y = 20, z = -9)

Вербальная форма	Графическая форма
Соотнести знаки координат x, y, z с данными табл. 2.3	Согласно табл. 2.3, это знаки 4-го октанта
Построить наглядное (аксонометрическое) изображение 4-го октанта
Определить механизм совмещения плоскостей
Построить комплексный чертеж 4-го октанта
Отложить координаты точки на осях: x = 5, y = 20, z = -9

 

Перенести координаты точки на оси комплексного чертежа
Построить горизонтальную, фронтальную и профильную проекции точки А (табл. 2.4)
Построить проекции точки А (А1, А2, А3) на комплексном чертеже (табл. 2.4)

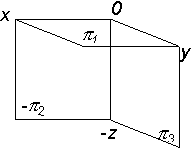
В следующих главах мы будем рассматривать образы: прямые и плоскости только в первой четверти. Хотя все рассматриваемые способы можно применить в любой четверти.

Выводы

Таким образом, на основании теории Г. Монжа, можно преобразовать пространственное изображение образа (точки) в плоскостное.

Эта теория основывается на следующих положениях:

1. Все пространство делится на 4 четверти с помощью двух взаимно перпендикулярных плоскостей p₁ и p₂, либо на 8 октантов при добавлении третьей взаимно-перпендикулярной плоскости p₃.

2. Изображение пространственного образа на эти плоскости получается с помощью прямоугольного (ортогонального) проецирования.

3. Для преобразования пространственного изображения в плоскостное считают, что плоскость p₂ – неподвижна, а плоскость p₁ вращается вокруг оси x так, что положительная полуплоскость p₁ совмещается с отрицательной полуплоскостью p₂, отрицательная часть p₁ – с положительной частью p₂.

4. Плоскость p₃ вращается вокруг оси z (линии пересечения плоскостей) до совмещения с плоскостью p₂ (см. рис. 2.31).

Изображения, получающиеся на плоскостях p₁, p₂ и p₃ при прямоугольном проецировании образов, называются проекциями.

Плоскости p₁, p₂ и p₃ вместе с изображенными на них проекциями, образуют плоскостной комплексный чертеж или эпюр.

Линии, соединяющие проекции образа ^ осям x, y, z, называются линиями проекционной связи.

Для более точного определения образов в пространстве может быть применена система трех взаимно перпендикулярных плоскостей p₁, p ₂, p ₃.

В зависимости от условия задачи можно выбрать для изображения либо систему p₁, p₂, либо p₁, p₂, p₃.

Систему плоскостей p₁, p₂, p₃ можно соединить с системой декартовых координат, что дает возможность задавать объекты не только графическим или (вербальным) образом, но и аналитическим (с помощью цифр).

Такой способ изображения образов, в частности точки, дает возможность решать такие позиционные задачи, как:

• расположение точки относительно плоскостей проекций (общее положение, принадлежность плоскости, оси);
• положение точки в четвертях (в какой четверти расположена точка);
• положение точек относительно друг друга, (выше, ниже, ближе, дальше относительно плоскостей проекций и зрителя);
• положение проекций точки относительно плоскостей проекций (равноудаление, ближе, дальше).

Метрические задачи:

• равноудаленность проекции от плоскостей проекций;
• отношение удаления проекции от плоскостей проекций (в 2–3 раза, больше, меньше);
• определение расстояния точки от плоскостей проекций (при введении системы координат).

Вопросы для самоанализа

1. Линией пересечения каких плоскостей является ось z?

2. Линией пересечения каких плоскостей является ось y?

3. Как располагается линия проекционной связи фронтальной и профильной проекции точки? Покажите.

4. Какими координатами определяется положение проекции точки: горизонтальной, фронтальной, профильной?

5. В какой четверти располагается точка F (10; –40; –20)? От какой плоскости проекций точка F удалена дальше всего?

6. Расстоянием от какой проекции до какой оси определяется удаление точки от плоскости p₁? Какой координатой точки является это расстояние?

Основные понятия, которые необходимо знать:

– система двух и трех плоскостей проекций;

– фронтальная проекция, горизонтальная проекция, профильная проекция, комплексный чертеж (эпюр);

– линии проекционной связи.

Способы деятельности, которыми надо уметь пользоваться:

• алгоритм построения точки, заданной координатами в системе трех плоскостей проекций в пространстве и на комплексном чертеже;
• построение третьей проекции по двум заданным.

Контрольные задания

1. Дать сравнительный анализ положения проекций точек в четвертях (см. табл. 2.5): по сходству, различию, противоположности (рис. 2.33 и рис. 2.34).

Задача № 1

Определить координаты точек и их взаимное положение в пространстве (рис. 2.33 и рис. 2.34)

Рис. 2.33	Рис. 2.34

Задача № 2

Построить проекции точки:

1. расположенной во II четверти и равноудаленной от всех трех плоскостей проекций;

2. расположенной в IV четверти, расстояние которой от плоскости p₁=0.