Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обозначения теоретико-множественныеСодержание книги
Поиск на нашем сайте
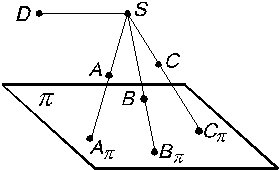
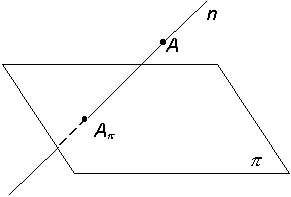
Сущность метода проецирования заключается в том, что проекция Аp некоторого геометрического образа А получается в результате пересечения проецирующей линии n, проходящей через точку А с плоскостью проекций p (рис.1.1):
Рис. 1.1
p – плоскость проекций; А – геометрический образ пространства; n – проецирующая линия; Аp = n Для получения проекции линии проецируют ряд ее точек с последующим соединением полученных проекций точек (рис. 1.2). Знание построения проекций точек и линий позволяет перейти к проецированию поверхности тела.
Рис. 1.2
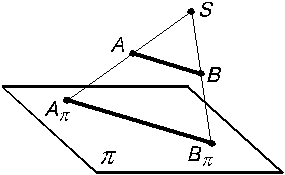
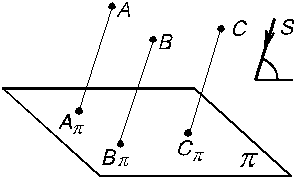
Способ проецирования В начертательной геометрии рассматриваются два основных способа проецирования: центральное и параллельное. Проецирование центральное Центральным называется проецирование, при котором все проецирующие лучи выходят из одной точки S, называемой центром проецирования. На рис. 1.3 дан пример центрального проецирования, где p – плоскость проекций; S – центр проецирования (точка, не лежащая в плоскости p); А, В, С – точки пространства; Аp, Вp, Сp – центральные проекции точек А, В, С, на плоскость p: они получаются в пересечении проецирующих лучей SA, SB, SC c плоскостью проекций. Если для некоторой точки D проецирующий луч окажется параллельным плоскости проекций, то принято считать, что они пересекаются, но в бесконечно удаленной точке. Проекцией точки D будет бесконечно удаленная точка Dp. Проекции точек (А и В), лежащих на одном проецирующем луче, совпадают (Аp
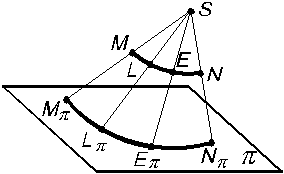
Построение центральных проекций прямой линии АВ и кривой MN показано на (рис. 1.5 и 1.6).
Проецирование параллельное Параллельным называется проецирование, при котором все проецирующие лучи между собой параллельны. Параллельные проекции могут быть косоугольными (рис.1.7) и прямоугольными (рис. 1.8).
S – направление проецирования. При косоугольном проецировании проецирующие лучи составляют с плоскостью проекций угол, не равный 90°. При прямоугольном проецировании проецирующие лучи перпендикулярны плоскости проекций (прямоугольное проецирование чаще всего называют ортогональным проецированием). Каждый из рассматриваемых способов имеет свои преимущества и недостатки. В зависимости от того, для какой цели выполняется чертеж, используется тот или иной способ. Для выполнения чертежа, по которому изготовляется изображаемый предмет, используется ортогональное проецирование. Косоугольное, параллельное проецирование используется в основном для получения аксонометрических изображений, центральное – для построения перспективных изображений. В изучаемом курсе основное внимание будет уделено ортогональному проецированию.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 p I А – проекция геометрического образа пространства на плоскость проекций.
p I А – проекция геометрического образа пространства на плоскость проекций.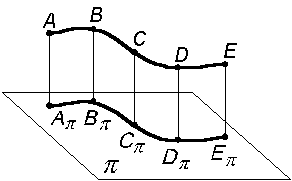
 Вp) (рис. 1.4).
Вp) (рис. 1.4).