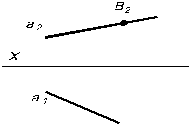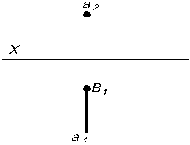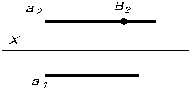Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение натуральной величины отрезка прямой общего положенияСодержание книги
Поиск на нашем сайте
Для определения натуральной величины отрезка прямой линии общего положения по ее проекциям применяют метод прямоугольного треугольника. Рассмотрим последовательность этого положения (табл. 3.4). Таблица 3.4
При решении подобной задачи находить натуральную величину отрезка можно только один раз (либо на p 1, либо на p 2). Если требуется определить углы наклона прямой к плоскостям проекций, то данное построение выполняется дважды – на фронтальной и горизонтальной проекциях отрезка. Принадлежность точки прямой
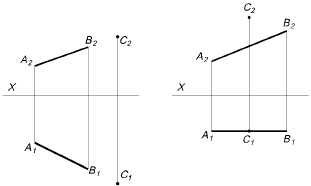
Задача № 1 Определить, принадлежит ли точка С отрезку прямой АВ.
Задача № 2 Найти вторую проекцию точки В, если она принадлежит прямой а (рис. 3.12–3.15)
Выводы На основе теории Монжа можно преобразовать пространственное изображение не только точки, но и более сложных объектов, в частности прямой линии и ее отрезка. Для получения проекций отрезка АВ строят проекции его концов-точек А и В – А1В1; А2В2; А3В3. Соединив одноименные проекции точек, получают проекции отрезка А1В1 – на плоскость p1; А2В2 – на плоскость p2; А3В3 – на плоскость p3. Проекции концов отрезков связаны линиями проекционной связи. Точка принадлежит отрезку, если ее проекции располагаются на одноименных проекциях этой же прямой. Отрезок прямой относительно плоскостей проекций может быть:
Отрезок может быть задан как в системе p1p 2, так и в p1p2p3. По двум заданным проекциям всегда можно построить третью. Отрезок в пространстве характеризуется длиной и углом наклона к плоскостям проекций. Для отрезков уровня и проецирующих эти величины определяются на самом комплексном чертеже, так как одна из проекций отрезка частного положения есть его натуральная величина. Для нахождения натуральной величины отрезка общего положения и углов его наклона к плоскостям проекций применяется метод прямоугольного треугольника. Вопросы для самоанализа 1. Что характерно для прямых, если они параллельны какой-либо плоскости проекции? 2. Какая проекция прямой будет параллельна оси Оx, если эта прямая параллельна p1? 3. Если одна из проекций прямой есть точка, что это за прямая? 4. Когда прямая проецируется на плоскость в натуральную величину? 5. Как определить натуральную величину отрезка общего положения?
Основные понятия, которые необходимо знать: – проекция прямой, отрезка; – отрезок общего положения; – прямые уровня (горизонталь, фронталь, профильная прямая); – проецирующие прямые (горизонтально проецирующая, фронтально проецирующая, профильно проецирующая прямая). Способы деятельности, которыми надо уметь пользоваться: 1. Построение третьей проекции отрезка по двум заданным.
Контрольные задания 1. Провести сравнительный анализ положения проекций прямых: а) по расположению относительно плоскостей проекций, осей; б) по сходству и различию.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.8 (0.005 с.) |

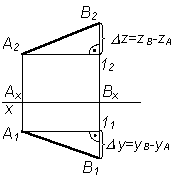
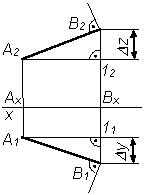
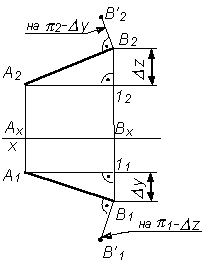
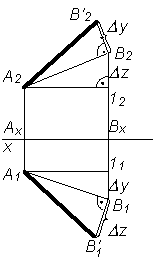

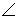 a – угол наклона отрезка АВ к плоскости p1;
a – угол наклона отрезка АВ к плоскости p1;
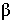 – угол наклона отрезка АВ к плоскости p2
– угол наклона отрезка АВ к плоскости p2
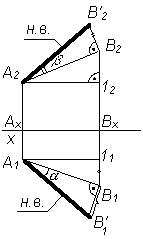
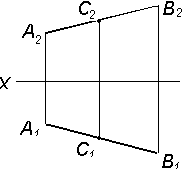 Рис. 3.4
Рис. 3.4