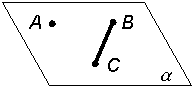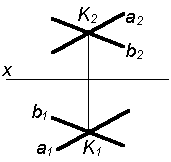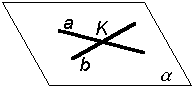
Алгоритм построения прямых пересекающихся

Вербальная форма	Графическая форма
1. Через точку К провести прямую h|| p1 и пересекающую прямую а
2. Через точку К (К2) проводим фронтальную проекцию горизонтали h2|| оси x: K2 h2
3. Отмечаем точку D (D2) пересечения горизонтали h2 и прямой a: D2=h2 a2
4. Находим горизонтальную проекцию точки D – D1
5. Проводим: К1D1 – горизонтальную проекцию горизонтали h1

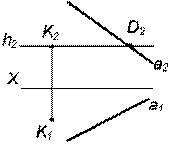
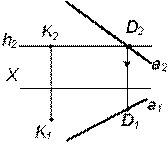
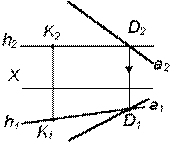
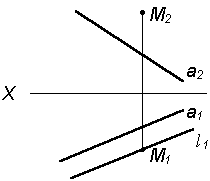
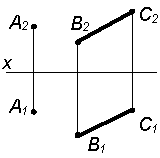
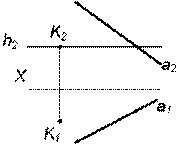
Таким образом, можно сделать следующий вывод, так как h₂ a₂=D₂, h₁ a₁=D₁, то эти прямые пересекаются.

Таблица 4.3

Алгоритм построения прямых параллельных

Вербальная форма	Графическая форма
1. Через точку М провести прямую l || a
2. Через точку М1 проведем l 1|| a1
3. Проведем l 2|| a2 через точку М2

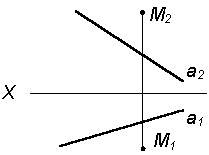
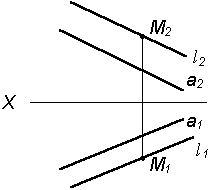
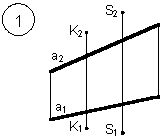
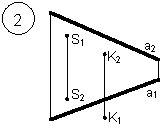
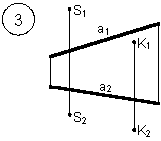
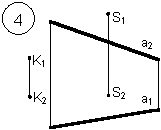
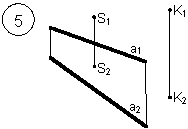
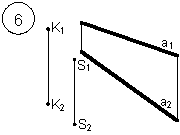
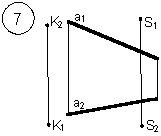
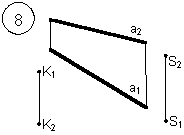
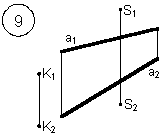
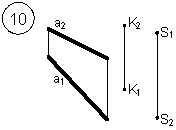
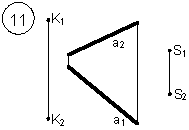
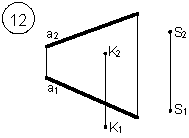
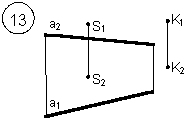
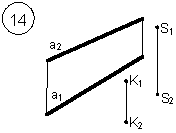
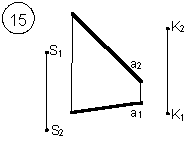
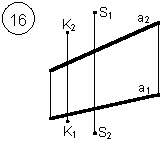
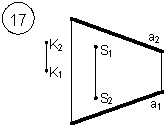
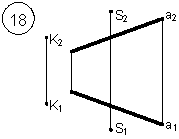
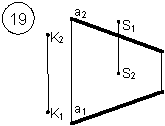
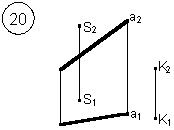
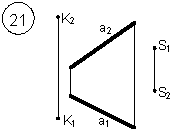
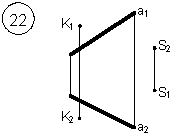
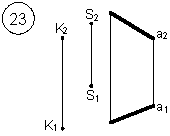
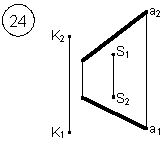
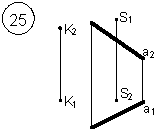
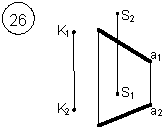
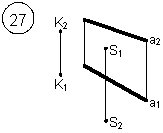
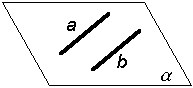
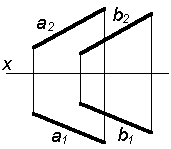
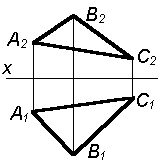
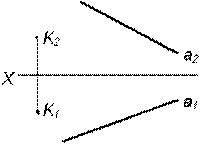
Таким образом, можно сделать следующий вывод: l параллельна а, так как l ₁ параллельна a₁ и l ₂ параллельна a₂.

Выводы

Прямые в пространстве могут быть:

– пересекающимися;

– параллельными;

– скрещивающимися.

Изображение этих прямых на комплексном чертеже характеризуется расположением их проекций, а именно:

1. если прямые пересекаются в пространстве, то на комплексном чертеже их одноименные проекции пересекаются, а точки пересечения их проекций лежат на одном перпендикуляре к оси проекций;

2. если прямые в пространстве параллельны, то на комплексном чертеже их одноименные проекции параллельны между собой;

3. если прямые скрещиваются в пространстве, то на комплексном чертеже их одноименные проекции пересекаются, но точки их пересечения не лежат на одном перпендикуляре к оси проекций.

Видимость прямых относительно плоскостей проекций определяется с помощью конкурирующих точек.

Используя изученный материал, можно решать на комплексном чертеже такие позиционные задачи, как:

– определять положение прямых и точек относительно друг друга и плоскостей проекций;

– выполнять построение прямых с заданными свойствами (параллельность, пересечение и т.п.).

Вопросы для самоанализа

1. В чем различие положений скрещивающихся и пересекающихся прямых в пространстве?

2. В чем сходство и различие положений проекций пересекающихся и скрещивающихся прямых на комплексном чертеже?

3. Если две прямые в пространстве имеют две общих точки, то они пересекаются. Верно ли это утверждение?

4. Приведите пример положения конкурирующих точек:

– двух скрещивающихся прямых;

– двух параллельных прямых.

5. Сколько проекций надо задать для определения параллельности прямых в пространстве? Рассмотрите варианты решения. Сделайте обобщенный вывод.

Основные понятия, которые необходимо знать:

– параллельность прямых;

– пересечение прямых;

– скрещивание прямых;

– совпадение прямых;

– конкурирующие точки.

Способы деятельности, которыми необходимо владеть:

1. Построение параллельных, пересекающихся, скрещивающихся прямых.

2. Построение прямых, параллельно заданным и построение прямых, пересекающих заданные.

Расчетно-графическая работа № 3
Взаимное положение прямых в пространстве

Задания выполняются в соответствии с вариантом.

1. Через точку К провести прямую h|| p₁ (четные варианты) или f|| p₂ (нечетные варианты) и прямую l, пересекающую заданную прямую а;

2. Через точку S провести прямую m || a.

Варианты РГР № 3

 

Примечание. Образец выполнения расчетно-графической работы № 3 см. прил. 4.

Глава 5

Плоскость

&	[4, гл. 3, § 16–19]; [5, гл. 8, § 46–48]; [6, гл. 3, § 8–10]; [7, гл. 3, подразделы 3.1–3.2]

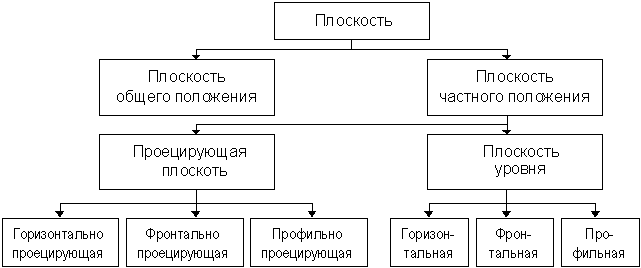
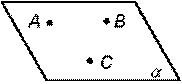
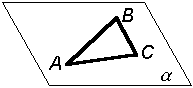
Общие положения

Плоскость – это двумерный геометрический образ, имеющий длину и ширину. Плоскость считается бесконечной, не имеющей толщины и непрозрачной. Плоскость является одним из наиболее часто встречающихся видов поверхности, которая содержит полностью каждую прямую, соединяющую любые две ее точки (рис. 5.1).

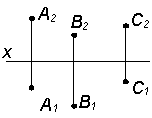
Рис. 5.1

§ 2. Способы задания плоскости

Плоскость на чертеже может быть задана следующими способами (табл. 5.1).

Таблица 5.1

Способ задания	Наглядное изображение	Комплексный чертеж
а) тремя точками, не лежащими на одной прямой

 

б) прямой и точкой вне данной прямой
в) двумя параллельными прямыми
г) плоской фигурой
д) двумя пересекаю- щимися прямыми
е) следом: Р ^ a