Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система трех взаимно перпендикулярных плоскостейСодержание книги
Поиск на нашем сайте
На практике исследования и построения изображений система двух взаимно перпендикулярных плоскостей не всегда дает возможность однозначного решения. Так, например, если переместить точку А вдоль оси Х, то ее изображение не изменится. Положение точки в пространстве (рис. 2.22) изменилось (рис. 2.24), а изображения на комплексном чертеже остались без изменений (рис. 2.23 и рис. 2.25).
Для решения данной задачи вводят систему трех взаимно перпендикулярных плоскостей, так как при составлении чертежей, например машин и их частей, требуется не два, а больше изображений. На этом основании в некоторые построения при решении задач необходимо вводить в систему p1, p2 и другие плоскости проекций.
Эти плоскости делят все пространство на VIII частей, которые называются октантами (от лат. okto восемь). Плоскости не имеют толщины, непрозрачны и бесконечны. Наблюдатель находится в первой четверти (для систем p1, p2) или первого октанта (для систем p1, p2, p3) в бесконечном удалении от плоскостей проекций. § 6. Точка в системе p1, p2, p3 Построение проекций некоторой точки А, расположенной в I октанте, на три взаимно перпендикулярные плоскости p1, p2, p3 показано на рис. 2.27. Используя совмещение плоскостей проекций с плоскостью p 2 и применяя способ вращения плоскостей, получаем комплексный чертеж точки А (рис. 2.28): АА1 ^ p1; АА 2 ^ p2; АА 3 ^ p3, где А3 – профильная проекция точки А; АХ, Аy, АZ – осевые проекции точки А. Проекции А1, А2, А3 называются соответственно фронтальной, горизонтальной и профильной проекцией точки А.
Плоскости проекций, попарно пересекаясь, определяют три оси x, y, z, которые можно рассматривать как систему декартовых координат: ось Х называется осью абцисс, ось y – осью ординат, ось Z – осью аппликат, точка пересечения осей, обозначаемая буквой О, есть начало координат. Так, зритель, рассматривающий предмет, находится в первом октанте. Для получения комплексного чертежа применим способ вращения плоскостей p1 и p3 (как показано на рис. 2.27) до совмещения с плоскостью p2. Окончательный вид всех плоскостей в первом октанте приведен на рис. 2.29.
Рис. 2.29 Здесь оси Оx и Оz, лежащие в неподвижной плоскости p2, изображены только один раз, ось Оy показана дважды. Объясняется это тем, что, вращаясь с плоскостью p1, ось y на эпюре совмещается с осью Оz, а вращаясь с плоскостью p3, эта же ось совмещается с осью Оx. Рассмотрим рис. 2.30, где точка пространства А, задана координатами (5,4,6). Эти координаты положительны, и сама она находится в первом октанте. Построение изображения самой точки и ее проекций на пространственной модели осуществляется с помощью координатного прямоугольного параллелограмма. Для этого на осях координат откладываем отрезки, соответственно отрезкам длины: ОАх = 5, OАy = 4, OАz = 6. На этих отрезках (ОАx, ОАy, ОАz), как на ребрах, строим прямоугольный параллелепипед. Одна из его вершин будет определять заданную точку А.
Рис. 2.30 Говоря о системе трех плоскостей проекций на комплексном чертеже (рис. 2.30), необходимо отметить следующее. Первое 1. две проекции точки принадлежат одной линии связи; 2. две проекции точки определяют положение третьей ее проекции; 3. линии связи перпендикулярны соответствующей оси проекций. Второе Любая точка пространства задается координатами. По знакам координат можно определить октант, в котором находится заданная точка. Для этого воспользуемся табл. 2.3, в которой рассмотрены знаки координат в 1–4 октантах (5–8 октанты не представлены, они имеют отрицательное значение х, а y и z повторяются). Таблица 2.3
Образование комплексного чертежа в системе трех плоскостей проекций осуществляется совмещением плоскостей p1, p2, p3 (рис. 2.31).
Рис. 2.31 Ось у в этом случае имеет два положения: y1 c плоскостью p1, y3 c плоскостью p3. Горизонтальная и фронтальная проекции точки располагаются на линии проекционной связи, перпендикулярной оси x, фронтальная и профильная проекции – на линии проекционной связи, перпендикулярной к оси z. А1АХ = А3АZ = АА2 – расстояние от А до p2 А2АХ = А3Аy = АА1 – расстояние отА до p1 А1Аy = А2АZ = АА3 – расстояние от А до p3 Расстояние точки от плоскости проекций измеряются аналогично отрезкам на эпюре (рис. 2.32).
Рис. 2.32 При построении проекции точки в пространстве и на комплексном чертеже могут применяться различные алгоритмы. 1. Алгоритм построения наглядного изображения точки, заданной координатами (рис. 2.30): 1.1. Соотнести знаки координат x, y, z с данными табл. 2.3. 1.2. Определить четверть, в которой расположена точка. 1.3. Выполнить наглядное (аксонометрическое) изображение четверти. 1.4. Отложить координаты точки на осях АХ, АY, АZ. 1.5. Построить проекции точки на плоскостях p1, p2, p3. 1.6. Построить перпендикуляры к плоскостям p1, p2, p3 в точках проекции А1, А2, А3. 1.7. Точка пересечения перпендикуляров есть искомая точка А. 2. Алгоритм построения комплексного чертежа точки в системе трех плоскостей проекций p 1, p 2, p 3, заданной координатами (рис. 2.32) 2.1. Определить по координатам четверть, в которой расположена точка. 2.2. Определить механизм совмещения плоскостей. 2.3. Построить комплексный чертеж четверти. 2.4. Отложить координаты точки на осях x, y, z (АХ, АY, АZ). 2.5. Построить проекции точки на комплексном чертеже.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.147.146 (0.006 с.) |





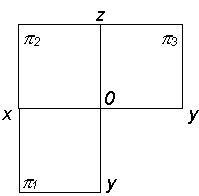
 Рис. 2.26
Рис. 2.26
 p2 = x; -x
p1
p2 = x; -x
p1