
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обозначение отношений между геометрическими образамиСодержание книги
Поиск на нашем сайте
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Рекомендовано Дальневосточным региональным учебно-методическим центром Рецензенты: Кафедра “Начертательная геометрия и машинная графика” Хабаровского государственного технического университета (Заведующий кафедрой, кандидат технических наук, доцент Л.Г. Вайнер) Доктор педагогических наук, заведующий кафедрой “Изобразительное искусство и начертательная геометрия” Хабаровского государственного педагогического университета, профессор А.И. Иконников
Учебное пособие составлено в соответствии с Государственным образовательным стандартом дисциплины “Инженерная графика”, раздел “Начертательная геометрия” для студентов первого курса. Изложены основы курса ортогонального проецирования. Рассмотрены алгоритмы решения позиционных задач на вербальном, графическом и аналитическом уровнях. Выделен основной понятийный аппарат, способы действий, которыми необходимо владеть, вопросы для самоанализа; даны различные виды задач, домашних заданий, итоговые расчетно-графические работы, тесты с целью самоанализа усвоения курса “Начертательная геометрия”. Предназначено для студентов первого курса ДВГУПС, обучающихся по специальностям 210700 “Автоматика, телемеханика и связь на ж.-д. транспорте”, 240100 “Организация перевозок и управление на транспорте”, направлению 657700 “Системы обеспечения движения поездов”, может быть полезно студентам инженерно-технических специальностей. a ГОУ ВПО “Дальневосточный государственный университет путей сообщения МПС России” (ДВГУПС), 2003 Оглавление Предисловие Введение Общие требования и методические рекомендации по изучению курса “начертательная геометрия” Методические указания по выполнению расчетно-графических работ Глава 1. Метод проекций § 1. Геометрические образы § 2. Способ проецирования § 3. Свойства ортогональных проекций § 4. Обратимость чертежа. Метод Монжа Выводы Вопросы для самоанализа Основные понятия, которые необходимо знать Глава 2. Проекция точки § 1. Система двух взаимно перпендикулярных плоскостей § 2. Точка в системе двух плоскостей проекций p 1 и p 2 § 3. Образование комплексного чертежа (эпюра) § 4. Характеристика положения точки в системе p 1 и p 2 § 5. Система трех взаимно перпендикулярных плоскостей § 6. Точка в системе p1, p2, p3 § 7. Комплексный чертеж и наглядное изображение точки в I–IV октантах Выводы Вопросы для самоанализа Основные понятия, которые необходимо знать Способы деятельности, которыми надо уметь пользоваться Контрольные задания Расчетно-графическая работа № 1. Построение наглядного изображения и комплексного чертежа точки в системе трех плоскостей проекций Глава 3. Прямая линия. Проецирование отрезка прямой линии § 1. Общие положения § 2. Прямая общего положения в системе трех плоскостей проекций p1, p2, p3 § 3. Прямые частного положения Прямые уровня Проецирующие прямые § 4. Построение третьей проекции отрезка по двум заданным § 5. Способ прямоугольного треугольника. Определение натуральной величины отрезка прямой линии и углов наклона прямой к плоскости проекции § 6. Определение натуральной величины отрезка прямой общего положения § 7. Принадлежность точки прямой Выводы Вопросы для самоанализа Основные понятия, которые необходимо знать Способы деятельности, которыми надо уметь пользоваться Контрольные задания Расчетно-графическая работа № 2. Определение натуральной величины отрезка прямой Глава 4. Взаимное положение прямых в пространстве § 1. Общие положения § 2. Определение видимости прямых относительно плоскостей проекций Выводы Вопросы для самоанализа Основные понятия, которые необходимо знать Способы деятельности, которыми необходимо владеть Расчетно-графическая работа № 3. Взаимное положение прямых в пространстве Глава 5. Плоскость § 1. Общие положения § 2. Способы задания плоскости § 3. Положение плоскости относительно плоскостей проекций § 4. Условия принадлежности прямой линии плоскости § 5. Прямые особого положения в плоскости § 6. Принадлежность точки плоскости Выводы Вопросы для самоанализа Основные понятия, которые необходимо знать Способы деятельности, которыми необходимо владеть Глава 6. Взаимное положение двух плоскостей, прямой линии и плоскости § 1. Взаимное положение двух плоскостей Параллельные плоскости Плоскости пересекающиеся § 2. Линия пересечения двух плоскостей общего положения Расчетно-графическая работа № 4. Построение линии пересечения двух плоскостей § 3. Прямая, параллельная плоскости § 4. Пересечение прямой линии с плоскостью общего положения § 5. Перпендикулярность прямой и плоскости § 6. Перпендикулярность двух плоскостей Выводы Вопросы для самоанализа Основные понятия, которые необходимо знать: Способы деятельности, которыми необходимо владеть: Расчетно-графическая работа № 5. Построение точки пересечения прямой и плоскости ТРЕНИНГ УМЕНИЙ Задачи для самостоятельной работы Тесты Заключение ПРИЛОЖЕНИЯ Приложение 1 Приложение 2 Приложение 3 Приложение 4 Приложение 5 Приложение 6 Краткий словарь специальных терминов и определений Рекомендуемый библиографический список Предисловие Любая цивилизация сильна культурой труда, умением работать. “Информационный взрыв” конца ХХ века прошлого тысячелетия привел к противоречию между количеством знаний, необходимых для успешной профессиональной деятельности и возможностью их осмысления. Ускорились темпы развития общественного производства, науки, культуры. Через каждые 6–7 лет знания устаревают. Поэтому наше время можно назвать веком образования. Система образования обеспечивает человека знаниями, позволяющими ему вписываться в создаваемый им мир, прогнозировать дальнейшее развитие этого мира и своего места в нем. Объективные закономерности общественного развития – научно техническая революция, информационный взрыв, внедрение принципиально-новых технологий, возрастание роли творческих элементов в различных областях человеческой деятельности – диктуют необходимость повышения интеллектуального потенциала каждого человека, развития инновационного стиля мышления, нестандартных способов осуществления любой деятельности каждого человека способного самостоятельно воспринимать и оценивать новую информацию, принимать решения, генерировать новые идеи. Творческие умения человека развиваются посредством разнообразных приемов и методов обучения при активном использовании имеющихся знаний и умений в конкретной учебной деятельности. Человеческое общество знает множество способов передачи информации, одним из которых является графическое изображение. Задачи строительства различных сооружений, крепостных укреплений, жилья, храмов, требовали предварительного построения изображений этих сооружений. Поэтому, зародившись в глубокой древности, различные способы построения изображений по мере развития материальной жизни общества претерпевали глубокие изменения. От примитивных изображений, передававших геометрические формы изображаемых объектов лишь весьма приближенно, постепенно совершался переход к составлению проекционных чертежей, отражающих их геометрические свойства. Первые попытки проекционных изображений уходят своими истоками в отдаленные времена жизни народов – еще до нашей эры. Одним из наиболее древних письменных произведений, дошедших до нас, является трактат римского архитектора Марка Витрувия (I век до н. э.) “Десять книг об архитектуре”. В этом произведении применение горизонтальных и фронтальных проекций дается как нечто уже известное. В этом же произведении Витрувий рассматривает вопросы, относящиеся к построению перспективных изображений. После упадка и застоя в Средние века в эпоху Возрождения начинается новый расцвет культуры. К концу 17 века был накоплен большой опыт по теории и практике изображения пространственных предметов на плоскости. Это позволило французскому геометру Гаспару Монжу (1746–1881) систематизировать и обобщить весь материал и издать научный труд под названием “Начертательная геометрия”. В своем труде Монж успешно решает проблему получения изображения на плоскости, которое позволило, во-первых, передавать информацию о форме и размерах предмета без искажения, а во-вторых, добиться однозначности и взаимозаменяемости получения изображений. Другими словами, на основе созданной им теории можно построить изображение любого предмета и, наоборот, по изображению предмета (эскиз, чертеж, рисунок) выполнить его в натуре. Предлагаемое учебное пособие по начертательной геометрии включает основополагающие разделы курса, предусмотренные учебной программой, содержит краткие теоретические положения, различные виды заданий и задач и алгоритмы их решения. После каждого раздела даются вопросы для самоанализа, основные понятия и способы деятельности, которые необходимо знать студенту и уметь ими пользоваться, а также расчетно-графические работы. Для лучшего усвоения учебного материала имеется тренинг умений, который включает задачи для самостоятельного выполнения по каждой главе и заключительное тестирование по всему курсу. Кроме того, для удобства пользования учебное пособие снабжено кратким словарем специальных терминов и определений. Автор выражает признательность и благодарность редактору Долгавиной Э.Г. за неоценимую помощь в процессе подготовки к изданию настоящего пособия. Введение Графическая деятельность требует выполнения ряда мыслительных и познавательных действий, качественное воплощение которых осуществляется при наличии у обучающихся способностей к восприятию различных средств графической информации, ее переработке, переосмыслению, анализу целостности восприятия. Все это позволяет создать образы реально существующего или задуманного объекта или явления с последующим его отображением в виде чертежа, рисунка, схемы, графика и т.д. Уровень графической подготовки человека сейчас определяется не столько техникой графических изображений, а тем, насколько он готов к мыслительным преобразованиям этих изображений и насколько развита подвижность образного мышления, а также уровень пространственных представлений, которые являются одним из показателей общего умственного развития. Начертательная геометрия как наука изучает вопросы отображения геометрических образов на плоскость. Под геометрическими образами понимают точки, линии (прямые и кривые), поверхности, плоскости. Совокупность этих образов дает любую пространственную форму (деталь, конструкцию, сооружение). Полученное изображение на плоскости называют чертежом. По образному выражению В. Курдюмова, чертеж – язык техники, а начертательная геометрия – грамматика этого языка. Отсюда цели и задачи курса начертательной геометрии, в результате изучения которого студент должен знать: – правила составления, чтения и выполнения чертежа; – правила, приемы и способы графического решения задач, связанных с пространственными формами; уметь: – строить изображения пространственных форм на плоскости, то есть составлять чертеж; – решать графическим способом на чертеже ряд пространственных задач. Общие требования и методические рекомендации Приступая к изучению курса “Начертательная геометрия”, студенты должны помнить, что в предлагаемом учебном пособии изложены только основные теоретические положения. Поэтому для более детального изучения прорабатываемого материала необходима систематическая работа с рекомендуемой литературой. Учебное пособие построено таким образом, что в конце каждой главы содержатся выводы по изученным темам, даются вопросы для самоанализа и заключительные расчетно-графические работы, выделены основные ключевые понятия и виды деятельности, которые студент должен знать, уметь владеть и пользоваться ими. Новый материал сопровождается достаточным количеством подробно разработанных примеров решения задач и упражнений. Решение задач и выполнение чертежей предполагает усвоение способов их выполнения. Для этого учебное пособие содержит алгоритмы выполнения заданий, которые даны в трех уровнях: вербальном (словесном), графическом и аналитическом. В рабочей тетради, представленной студентом на проверку преподавателю, помимо решенных задач, должны быть записи основных теоретических положений и записи последовательности производимых на чертеже операций с помощью символов, то есть должны быть составлены алгоритмы их решения (комбинирование известных способов деятельности, выбор оптимального варианта). На последнем практическом занятии студент получает допуск к экзамену при условии, что все пять расчетно-графических работ (рекомендации по выполнению которых будут даны ниже), а также решенные задачи, выполненные по надлежащим правилам, будут сданы. Методические указания по выполнению 1. В первом семестре выполняется пять расчетно-графических работ (РГР), которые сдаются по мере изучения тем курса “Начертательная геометрия”. 2. Каждый студент выполняет свой вариант, выданный преподавателем. 3. Чертежи выполняются на листах чертежной бумаги формата А4, (210 х 297). Можно использовать масштаб. 4. Каждый лист оформляется рамкой и надписью по форме, приведенной в прил. 1. Все надписи, как и отдельные обозначения в виде букв и цифр, должны быть выполнены стандартным шрифтом размером 3,5 и 5. Условия задач и все геометрические построения выполняются карандашом при помощи чертежных инструментов. На тщательность построения должно быть обращено особое внимание. Небрежное выполнение построений не только снижает качество чертежа, но и приводит к неправильным результатам. Глава 1 Начертательная геометрия является наивысшим средством развития той таинственной способности человеческого духа, которая зовется воображением и которая является ступенью к другой царственной способности – фантазии, без которой почти не совершаются великие открытия и изобретения Н.А. Рынин
В основе правил построения изображений, рассматриваемых в начертательной геометрии и применяемых в черчении, лежит метод проекций. Изучение начинается с построения проекций точки, так как при построении изображений любой пространственной формы рассматривается ряд точек, принадлежащих этой форме. В настоящем учебном пособии приняты следующие буквенно-цифровые обозначения геометрических фигур. Геометрические образы 1. Плоскость проекций: p – произвольная; p1 – горизонтальная; p2 – фронтальная; p3 – профильная; S – центр проецирования. 2. Оси проекции: X – ось абсцисс; Y – ось ординат; Z – ось аппликат; Начало координат – прописной буквой О. 1. Точки, расположенные в пространстве, обозначаются прописными буквами латинского алфавита, а также арабскими цифрами: A, B, C, D,…, L, M, N, 1, 2, 3, 4,…,12, 13, 14,… 2. Линии, расположенные произвольно относительно плоскостей проекций, обозначаются строчными буквами латинского алфавита: a, b, c,…, l, m, n Линии уровня обозначаются: h – горизонталь; f – фронталь; p – профильная прямая. Для прямых линий используются также следующие обозначения: (A, B) – прямая, проходящая через точки A и B; [AB] – отрезок прямой, ограниченный точками А и В 3. Плоскости обозначаются прописными буквами латинского и греческого алфавита: P, Q, R, S, T, S, L, Q … Для обозначения плоскостей уровня используются прописные буквы только греческого алфавита: Г – горизонтальная плоскость (гамма); Ф – фронтальная плоскость (фи); Р – профильная плоскость (ро). Чтобы выделить способ задания плоскости, указывают ее геометрические элементы, которыми она определяется: P (D ABC) – плоскость P задана треугольником ABC; Q (a R (m II n) – плоскость R задана параллельными прямыми m и n; S (A,В,С) – плоскость S задана тремя точками. 4. Проекции точек, линий и других геометрических образов обозначаются теми же буквами (или цифрами), что и оригинал, но с добавлением индекса А1, А2, А3 или 11, 12, 13, соответствующего плоскости проекций, на которой они получены: А1, В1, С1, …, М1, N1… – горизонтальные проекции точек; А2, В2, С2, …, М2, N2… – фронтальные проекции точек; А3, В3, С3, …, М3, N3… – профильные проекции точек; a1, b1, c1, …, m1,n1… – горизонтальные проекции линий; a2, b2, c2, …, m2,n2… – фронтальные проекции линий; a3, b3, c3,…, m3,n3… – профильные проекции линий и т. д. Способ проецирования В начертательной геометрии рассматриваются два основных способа проецирования: центральное и параллельное. Проецирование центральное Центральным называется проецирование, при котором все проецирующие лучи выходят из одной точки S, называемой центром проецирования. На рис. 1.3 дан пример центрального проецирования, где p – плоскость проекций; S – центр проецирования (точка, не лежащая в плоскости p); А, В, С – точки пространства; Аp, Вp, Сp – центральные проекции точек А, В, С, на плоскость p: они получаются в пересечении проецирующих лучей SA, SB, SC c плоскостью проекций. Если для некоторой точки D проецирующий луч окажется параллельным плоскости проекций, то принято считать, что они пересекаются, но в бесконечно удаленной точке. Проекцией точки D будет бесконечно удаленная точка Dp. Проекции точек (А и В), лежащих на одном проецирующем луче, совпадают (Аp
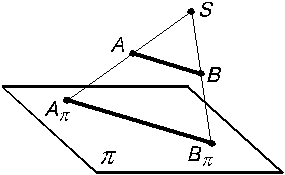
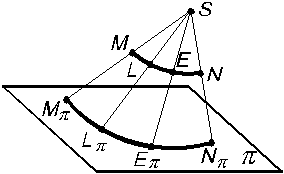
Построение центральных проекций прямой линии АВ и кривой MN показано на (рис. 1.5 и 1.6).
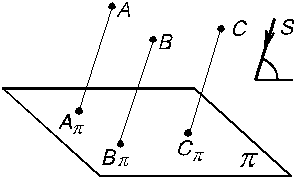
Проецирование параллельное Параллельным называется проецирование, при котором все проецирующие лучи между собой параллельны. Параллельные проекции могут быть косоугольными (рис.1.7) и прямоугольными (рис. 1.8).
S – направление проецирования. При косоугольном проецировании проецирующие лучи составляют с плоскостью проекций угол, не равный 90°. При прямоугольном проецировании проецирующие лучи перпендикулярны плоскости проекций (прямоугольное проецирование чаще всего называют ортогональным проецированием). Каждый из рассматриваемых способов имеет свои преимущества и недостатки. В зависимости от того, для какой цели выполняется чертеж, используется тот или иной способ. Для выполнения чертежа, по которому изготовляется изображаемый предмет, используется ортогональное проецирование. Косоугольное, параллельное проецирование используется в основном для получения аксонометрических изображений, центральное – для построения перспективных изображений. В изучаемом курсе основное внимание будет уделено ортогональному проецированию. Выводы Начертательная геометрия как наука изучает вопросы изображений геометрических образов (точки, линии, плоскости, поверхности) на плоскости. Основным методом начертательной геометрии является метод проецирования. Способы проецирования могут быть центральными, параллельными (ортогональными и косоугольными). Вопросы для самоанализа 1. На каком методе базируется начертательная геометрия? 2. Назовите способы проецирования. Дайте их определения. В чем суть каждого из них? 3. Назовите свойства проекций: а) центральных; б) параллельных косоугольных; в) ортогональных. 4. Можно ли ортогональное проецирование назвать параллельным? 5. В чем заключается метод Монжа?
Основные понятия, которые необходимо знать:
Глава 2 Проекция точки
Задача № 1. Построить комплексный чертеж точки А, если: 1. точка расположена во II четверти и равноудалена от плоскостей p1 и p2. 2. точка расположена в III четверти, и ее расстояние до плоскости p1 в два раза больше, чем до плоскости p2. 3. точка расположена в IV четверти, и ее расстояние до плоскости p1 больше, чем до плоскости p2. Задача № 2. Определить, в каких четвертях расположены точки (рис. 2.21).
Рис. 2.21 Задача № 3. 1. Построить наглядное изображение точек в четвертях: а) А – общего положения в III четверти; б) В – общего положения в IV четверти; в) С – во второй четверти, если ее расстояние от p1 равно 0; г) D – в I четверти, если ее расстояние от p2 равно 0. Задача № 4. Построить комплексный чертеж точек А, В, С, D (см. задачу 3). Первое 1. две проекции точки принадлежат одной линии связи; 2. две проекции точки определяют положение третьей ее проекции; 3. линии связи перпендикулярны соответствующей оси проекций. Второе Любая точка пространства задается координатами. По знакам координат можно определить октант, в котором находится заданная точка. Для этого воспользуемся табл. 2.3, в которой рассмотрены знаки координат в 1–4 октантах (5–8 октанты не представлены, они имеют отрицательное значение х, а y и z повторяются). Таблица 2.3
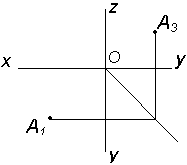
Образование комплексного чертежа в системе трех плоскостей проекций осуществляется совмещением плоскостей p1, p2, p3 (рис. 2.31).
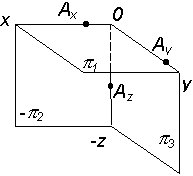
Рис. 2.31 Ось у в этом случае имеет два положения: y1 c плоскостью p1, y3 c плоскостью p3. Горизонтальная и фронтальная проекции точки располагаются на линии проекционной связи, перпендикулярной оси x, фронтальная и профильная проекции – на линии проекционной связи, перпендикулярной к оси z. А1АХ = А3АZ = АА2 – расстояние от А до p2 А2АХ = А3Аy = АА1 – расстояние отА до p1 А1Аy = А2АZ = АА3 – расстояние от А до p3 Расстояние точки от плоскости проекций измеряются аналогично отрезкам на эпюре (рис. 2.32).
Рис. 2.32 При построении проекции точки в пространстве и на комплексном чертеже могут применяться различные алгоритмы. 1. Алгоритм построения наглядного изображения точки, заданной координатами (рис. 2.30): 1.1. Соотнести знаки координат x, y, z с данными табл. 2.3. 1.2. Определить четверть, в которой расположена точка. 1.3. Выполнить наглядное (аксонометрическое) изображение четверти. 1.4. Отложить координаты точки на осях АХ, АY, АZ. 1.5. Построить проекции точки на плоскостях p1, p2, p3. 1.6. Построить перпендикуляры к плоскостям p1, p2, p3 в точках проекции А1, А2, А3. 1.7. Точка пересечения перпендикуляров есть искомая точка А. 2. Алгоритм построения комплексного чертежа точки в системе трех плоскостей проекций p 1, p 2, p 3, заданной координатами (рис. 2.32) 2.1. Определить по координатам четверть, в которой расположена точка. 2.2. Определить механизм совмещения плоскостей. 2.3. Построить комплексный чертеж четверти. 2.4. Отложить координаты точки на осях x, y, z (АХ, АY, АZ). 2.5. Построить проекции точки на комплексном чертеже. Пример построения третьей проекции точки по двум заданным Точка в пространстве определяется любыми двумя своими проекциями. При необходимости построения третьей проекции по двум заданным необходимо воспользоваться соответствием отрезков линий проекционной связи, полученных при определении расстояний от точки до плоскости проекций (см. рис. 2.27 и рис. 2.28). Примеры решения задач в I октанте
Рассмотрим алгоритм построения точки А (табл. 2.5) Таблица 2.5 Алгоритм построения точки А
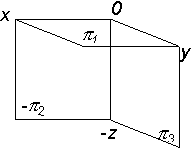
В следующих главах мы будем рассматривать образы: прямые и плоскости только в первой четверти. Хотя все рассматриваемые способы можно применить в любой четверти. Выводы Таким образом, на основании теории Г. Монжа, можно преобразовать пространственное изображение образа (точки) в плоскостное. Эта теория основывается на следующих положениях: 1. Все пространство делится на 4 четверти с помощью двух взаимно перпендикулярных плоскостей p1 и p2, либо на 8 октантов при добавлении третьей взаимно-перпендикулярной плоскости p3. 2. Изображение пространственного образа на эти плоскости получается с помощью прямоугольного (ортогонального) проецирования. 3. Для преобразования пространственного изображения в плоскостное считают, что плоскость p2 – неподвижна, а плоскость p1 вращается вокруг оси x так, что положительная полуплоскость p1 совмещается с отрицательной полуплоскостью p2, отрицательная часть p1 – с положительной частью p2. 4. Плоскость p3 вращается вокруг оси z (линии пересечения плоскостей) до совмещения с плоскостью p2 (см. рис. 2.31). Изображения, получающиеся на плоскостях p1, p2 и p3 при прямоугольном проецировании образов, называются проекциями. Плоскости p1, p2 и p3 вместе с изображенными на них проекциями, образуют плоскостной комплексный чертеж или эпюр. Линии, соединяющие проекции образа ^ осям x, y, z, называются линиями проекционной связи. Для более точного определения образов в пространстве может быть применена система трех взаимно перпендикулярных плоскостей p1, p 2, p 3. В зависимости от условия задачи можно выбрать для изображения либо систему p1, p2, либо p1, p2, p3. Систему плоскостей p1, p2, p3 можно соединить с системой декартовых координат, что дает возможность задавать объекты не только графическим или (вербальным) образом, но и аналитическим (с помощью цифр). Такой способ изображения образов, в частности точки, дает возможность решать такие позиционные задачи, как:
Метрические задачи:
Вопросы для самоанализа 1. Линией пересечения каких плоскостей является ось z? 2. Линией пересечения каких плоскостей является ось y? 3. Как располагается линия проекционной связи фронтальной и профильной проекции точки? Покажите. 4. Какими координатами определяется положение проекции точки: горизонтальной, фронтальной, профильной? 5. В какой четверти располагается точка F (10; –40; –20)? От какой плоскости проекций точка F удалена дальше всего? 6. Расстоянием от какой проекции до какой оси определяется удаление точки от плоскости p1? Какой координатой точки является это расстояние? Основные понятия, которые необходимо знать: – система двух и трех плоскостей проекций; – фронтальная проекция, горизонтальная проекция, профильная проекция, комплексный чертеж (эпюр); – линии проекционной связи. Способы деятельности, которыми надо уметь пользоваться:
Контрольные задания 1. Дать сравнительный анализ положения проекций точек в четвертях (см. табл. 2.5): по сходству, различию, противоположности (рис. 2.33 и рис. 2.34). Задача № 1 Определить координаты точек и их взаимное положение в пространстве (рис. 2.33 и рис. 2.34)
Задача № 2 Построить проекции точки: 1. расположенной во II четверти и равноудаленной от всех трех плоскостей проекций; 2. расположенной в IV четверти, расстояние которой от плоскости p1=0. Варианты РГР № 1
Примечание.
Глава 3
Общие положения Линия – это одномерный геометрический образ, имеющий длину; множество всех последовательных положений движущейся точки. По определению Эвклида: "Линия же – длина без ширины". Положение прямой линии в пространстве определяется положением двух ее точек. Чтобы спроецировать прямую линию в общем случае, надо спроецировать две ее точки и соединить полученные проекции. Прямая в пространстве может быть расположена произвольно. Рассмотрим различные положения прямой относительно плоскостей проекций p1, p2, p3 (рис. 3.1).
Рис. 3.1 § 2. Прямая общего положения в системе трех плоскостей проекций p 1, p 2, p 3
Прямые частного положения Прямые частного положения – это прямые, которые либо параллельны (табл. 3.1), либо перпендикулярны одной из плоскостей проекций (табл. 3.2). Прямые уровня Всякую линию, параллельную плоскости проекций, называют линией уровня. В начертательной геометрии различают три основные линии уровня: горизонталь, фронталь и профильную линии (табл. 3.1). Таблица 3.1 Прямые уровня
|

 b) – плоскость Q задана пересекающимися прямыми a и b;
b) – плоскость Q задана пересекающимися прямыми a и b; Вp) (рис. 1.4).
Вp) (рис. 1.4).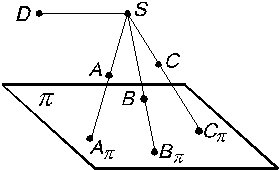























 – угол наклона к p1
– угол наклона к p1





