
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение третьей проекции отрезка по двум заданнымСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В нашем примере мы будем рассматривать построение прямой общего положения в первой четверти (табл. 3.3). Таблица 3.3
Задача № 1 При решении задач использовать алгоритм построения третьей проекции прямой по двум заданным (табл. 3.3). 1. По двум заданным проекциям построить третью на рис. 3.1–3.9:
Задача № 2 Определить, на каком из комплексных чертежей данная прямая является натуральной величиной отрезка. Где можно определить углы наклона прямой к плоскостям проекций (рис. 3.1–рис. 3.9)? Способ прямоугольного треугольника. Определение натуральной величины отрезка прямой линии и углов наклона прямой к плоскостям проекций Построение проекций отрезка прямой общего и частного положения позволяет решать не только позиционные задачи (расположение относительно плоскостей проекций), но и метрические – определение длины отрезка и углов наклона к плоскостям проекций. Но эта задача может быть решена только в случае, если отрезок параллелен или перпендикулярен к одной или нескольким плоскостям. Рассмотрим способ решения такой задачи для отрезка общего положения. Пусть дан отрезок АВ общего положения относительно плоскостей p1 и p2. АВ'В – прямоугольный треугольник (рис. 3.10), в котором катет АВ' = А1В1 (проекции отрезка АВ на плоскость p1), а катет ВВ' равен z – разности расстояний точек А и В до плоскости p1. Угол a в прямоугольном треугольнике АВ'В определяет угол наклона прямой АВ к плоскости p1. Рассмотрим треугольник ВА'А (рис. 3.11), где катет ВА' равен проекции А2В2 (ВА' = А2В2), а второй катет АА' равен D y – разности расстояний точек А и В от плоскости p 2. Угол Таким образом, натуральная длина отрезка прямой общего положения определяется гипотенузой прямоугольного треугольника, у которого один катет равен проекции отрезка, а второй катет – алгебраической разности расстояний от концов отрезка до одной из плоскостей проекций.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 889; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |













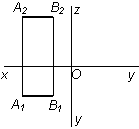




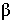 в прямоугольном треугольнике ВАА' определяет угол наклона прямой АВ к плоскости p2.
в прямоугольном треугольнике ВАА' определяет угол наклона прямой АВ к плоскости p2.




