Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение кривых Бернштейна-БезьеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Кривая Безье задается многоугольником и имеет математическое параметрическое представление вида:
Алгоритм де Кастельжопа В вычислительной математике алгоритм де Кастельжо, названный в честь его изобретателя Поля де Кастельжо — рекурсивный метод определения формы многочленов Бернштейна или кривых Безье. Алгоритм де Кастельжо также может быть использован для разделения кривой Безье на две части по произвольному значению параметра. Достоинством алгоритма является его более высокая вычислительная устойчивость по сравнению с прямым методом.
Неоднородные рациональные B-сплайны Неоднородный рациональный В-сплайн (NURBS – nonuniform rational B-spline curve) подобен обычному неоднородному В-сплайну, так как основан на тех же функциях сопряжения, получаемых для неоднородных узлов. Впервые описание рациональных кривых и поверхностей было предложено Кунсом (Coons, 1967). Рациональные В-сплайны это единственное точное математическое представление, охватывающее все аналитические формы: прямые, плоскости, конические сечения (включая окружности), кривые произвольной формы, квадрики и трехмерные модели, используемые в компьютерной графике и проектировании. Рациональные В-сплайны применяются в ряде систем геометрического моделирования и реализованы аппаратно в некоторых рабочих станциях. 32. Преобразования кривых Бернштейна-Безье Кривы́е Безье́ или Кривы́е Бернште́йна-Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Pierre Bézier) из автомобилестроительной компании «Рено» и Полем де Кастельжо (Paul de Faget de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей. Линейные кривые Параметр t в функции, описывающей линейный случай кривой Безье, определяет, где именно на расстоянии от P0 до P1 находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точкамиP0 и P1. Квадратичные кривые Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия, чтобы параметр t изменялся от 0 до 1: Кривые высших степеней Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0
33. Аффинное преобразование и его матричное представление Аффинным называется преобразование плоскости, переводящее каждую прямую в прямую и параллельные прямые а параллельные. Преобразование называется взаимно однозначным, если - разные точки переходят в разные; - в каждую точку переходит какая-то точка. , например, сжатие 0 разжатие, поворот, перенос и тд
Матрица 3x3, последний столбец которой равен (0 0 1)T, задает аффинное преобразование плоскости: [ * * 0 ] [ * * 0 ] [ * * 1 ] По одному из свойств, аффинное преобразование можно записать в виде: f(x) = x * R + t, где R – обратимая матрица 2x2, а t – произвольный вектор. 34. Виды аффинных преобразований
Сжатие, растяжение, поворот, перенос, движение, наклон, отображение
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.42.41 (0.006 с.) |

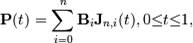
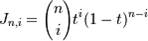
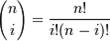
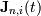 - это i-тая функция базиса Бернштейна порядка n. Здесь i — порядковый номер опорной вершины, n — порядок определяющей функции базиса Бернштейна — и, следовательно, сегмента полиномиальной кривой, на единицу меньше количества точек определяющего многоугольника.
- это i-тая функция базиса Бернштейна порядка n. Здесь i — порядковый номер опорной вершины, n — порядок определяющей функции базиса Бернштейна — и, следовательно, сегмента полиномиальной кривой, на единицу меньше количества точек определяющего многоугольника. 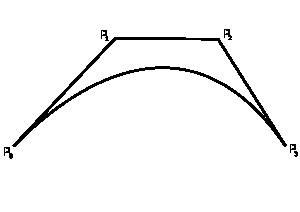
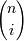 - биномиальные коэффициенты.
- биномиальные коэффициенты. 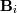 - функция компонент векторов опорных вершин (координаты вершин многоугольника Безье).
- функция компонент векторов опорных вершин (координаты вершин многоугольника Безье). 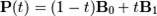
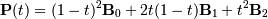

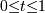
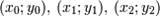 преобразовывается в кубическую кривую Безье с координатами
преобразовывается в кубическую кривую Безье с координатами