
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проектирование переходных кривых.Содержание книги
Поиск на нашем сайте
Прямые и круговые кривые во избежание внезапного появления центробежной силы должны сопрягаться плавно с помощью переходных кривых. Основное назначение переходных кривых заключается в обеспечении плавного изменения центробежных сил при входе экипажей в круговую кривую и выходе из неё. На их протяжении осуществляют плавные отводы возвышения наружной рельсовой нити и уширения колеи в круговой кривой. Схема переходной кривой в увязке с отводом возвышения наружной рельсовой нити и изменением центробежной силы представлена на рисунке 2.4.
\
Рисунок 2.4 – схема переходной кривой: а – изменение возвышения наружной рельсовой нити над внутренней; б – план участка пути с переходной кривой (по оси пути); в – изменение центробежной силы. В качестве переходных кривых чаще всего используют радиоидальные спирали и реже – кубические параболы. У этих кривых кривизна Кх изменяется плавно, увеличиваясь пропорционально их длине lx:
где: С – коэффициент пропорциональности, называемый параметром переходной кривой; ρх - радиус кривизны. Учитывая, что до конца переходной кривой lx=l0 и ρx=R, параметр переходной кривой определяется как:
Длина переходной кривой l0 орределяется из условийограничения вертикальной составляющей скорости подъема колеса на наружный рельс f и скорости нарастания поперечного ускорения ψ. Непогашенное горизонтальное ускорение определяется:
Длина переходной кривой должна удовлетворять условию:
[f]=28…45мм/с. Из табл. 2.5 /3/ для максимальной скорости пассажирских поездов Vmax п =120 км/ч рекомендуемый уклон отвода возвышения [ i ]=0,0008‰. Длина переходной кривой определяется по формуле:
где: h – величина возвышения наружного рельса, мм.
Получив значение
Тогда по формуле (2.17) С=750 ·160=120000 м2. Проверка: 1,602·С5/9=1063м. R<1063м. Делаем вывод, что переходная кривая будет иметь вид радиоидальной спирали.
Рисунок 2.5 – Схема разбивки переходных кривых методом сдвижки круговой кривой внутрь. Угол поворота
Во многих случаях значения m0 и p находят приблизительно, имея в виду что
φ0=6,3о
Возможность разбивки переходной кривой определяется по следующим зависимостям:
где:
Длина круговой кривой
Разбивка переходной кривой производится по радиоидальной спирали и координаты переходной кривой определяются по уравнениям:
(2.30)
(2.31)
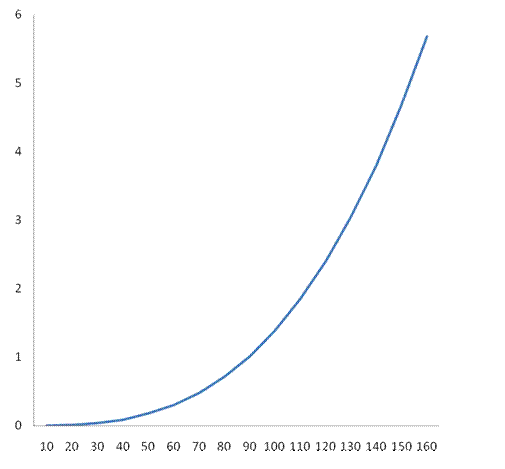
Расчеты координат переходной кривой ведутся в табличной форме (таблица 2.2).
Таблица 2.2 – Координаты переходной кривой по радиоидальной спирали.
По результатам таблицы 2.2 строится график переходной кривой (рисунок 2.5).
Рисунок 2.6 - График переходной кривой.
Расстояние m от начала переходной кривой до нового положения тангенсного столбика определяется по формуле: (2.32)
где: хк – конечная абсцисса переходной кривой, м.
Расстояние m0 от начала переходной кривой до первоначального положения тангенсного столбика определяется по формуле:
где: р – величина сдвижки, на которую производят разбивку переходных кривых на местности по ранее намеченной круговой кривой внутрь, м.
Величина сдвижки определяется по формуле:
Полная длина новой кривой (с переходными кривыми) определяется по формуле:
Суммированный тангенс новой кривой:
(2.36)
Суммированная биссектриса:
Домер:
Разбивку переходных и круговых кривых на местности производят геодезическими способами.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

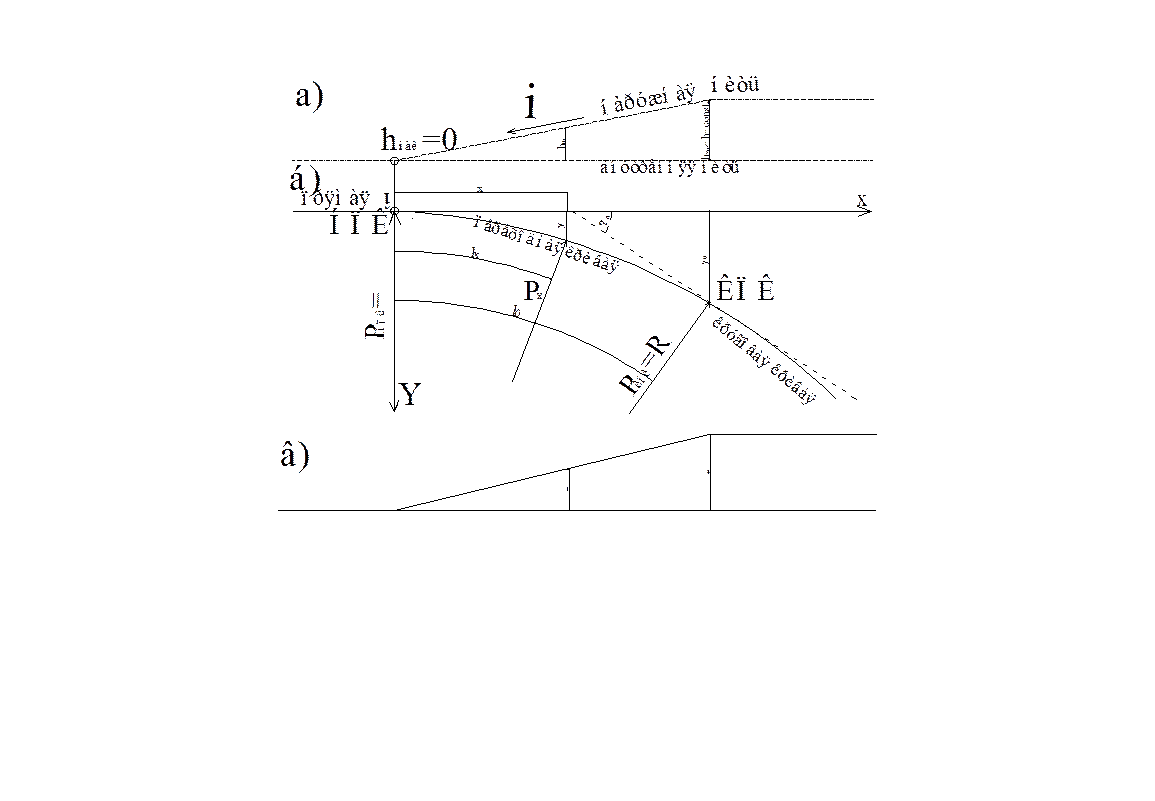
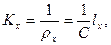 (2.16)
(2.16)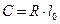 . (2.17)
. (2.17)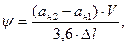 (2.18)
(2.18)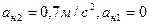 и
и 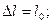 ψ≤[ψ]=0,6 м/с3.
ψ≤[ψ]=0,6 м/с3. 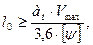 (2.19)
(2.19)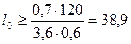 м
м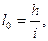 (2.23)
(2.23)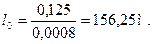
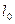 окгуглим до величины, кратной 10 м в большую сторону:
окгуглим до величины, кратной 10 м в большую сторону: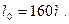

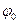 определяется по формуле:
определяется по формуле: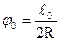 , (2.24)
, (2.24)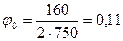 рад
рад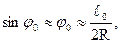 (2.25)
(2.25)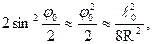 (2.26)
(2.26)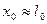 и
и 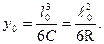 (2.27)
(2.27)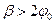 , (2.28)
, (2.28)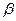 - угол поворота трассы, рад.
- угол поворота трассы, рад.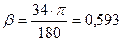 рад,
рад, 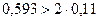
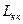 определяется по формуле:
определяется по формуле: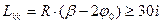 (2.29)
(2.29)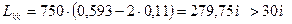
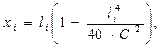
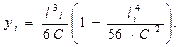
 , м
, м
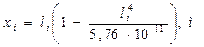
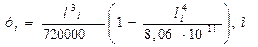
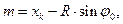
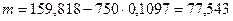 м
м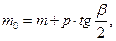 (2.33)
(2.33)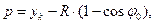 (2.34)
(2.34)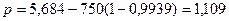 м
м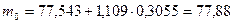 м
м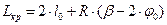 , (2.35)
, (2.35)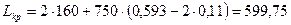 м
м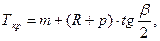
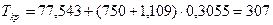 м
м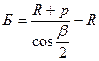 (2.37)
(2.37)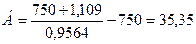 м
м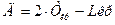 , (2.38)
, (2.38)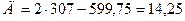 м
м


