Применение моделей кривых роста в экономическом прогнозировании

Комплекс аналитических методов выравнивания сводится к выбору конкретных кривых роста и определению их параметров. Под кривой роста будем понимать некоторую функцию, аппроксимирующую за­данный динамический ряд.

Разработка прогноза с использованием кривых роста включает сле­дующие этапы:

• выбор одной или нескольких кривых, форма которых соответствует динамике временного ряда;

• оценка параметров выбранных кривых;

• проверка адекватности выбранных кривых прогнозируемому процессу и окончательный выбор кривой;

• расчет точечного и интервального прогнозов.

Кривые роста обычно выбираются из трех классов функций.

К первому классу относятся кривые, которые используются для описания процессов с монотонным характером развития и отсутствием пределов роста.

Ко второму классу относятся кривые, имеющие предел роста в иссле­дуемом периоде. Такие кривые называют кривыми насыщения. Если кривые насыщения имеют точки перегиба, то они относятся к кривым третьего класса. Их называют S -образными кривыми. Среди кривых роста первого типа следует выделить класс полиномов:

y_t = a₀ + a ₁ t +a ₂ t ² +a ₃ t ³ + …

Параметр а₀ является начальным уровнем ряда при t = 0, а ₁называют линейным приростом, а ₂ — ускорением роста, а₃ — изменением ускоре­ния роста.

В экономических исследованиях в большинстве случаях применяются полиномы не выше третьего порядка.

Полином первой степени

y_t = a ₀ + a ₁ t

на графике (рис. 6.1) изображается в виде прямой и используется для описания процессов, развивающихся равномерно во времени.

 

 

 

Полином второй степени

y_t = a₀ + a ₁ t + а₂ t ²

на графике (рис. 6.2) изображается в виде параболы и применяется в тех случаях, когда процесс развивается равноускоренно. Если а₂ > О, то ветви параболы направлены вверх, в случае а₂ < О — вниз.

 

Полином третьей степени

		Рис. 6.3. Полином третьей степени

 

 

y_t = a₀ + a ₁ t + а ₂ t ² + a ₃ t ³

У этого полинома (рис. 6.3) знак прироста ординат может изменяться один или два раза. Оценки параметров полиномов определя­ются методом наименьших квадратов. Так, нормальное уравнение для определения ко­эффициентов прямой имеет вид

{

Σ y _t = a₀ n + a ₁ Σ t,

Σ y _t t = a₀ Σ t + a ₁ Σ t ²

Решение системы, т. е. нахождение коэффициентов системы а₀ и а₁, производится по формулам Крамера.

Систему нормальных уравнений можно упростить и уменьшить абсолютные значения величин, если перенести начала координат в середи­ну ряда динамики. Если до переноса начало координат t равно 1, 2, 3..., то после переноса получим:

• для четного числа членов t =…, -5, -3, -1, 1, 3, 5...,

• для нечетного числа членов t = …, -3, -2, -1, О, 1, 2, 3...
В этом случае коэффициенты прямой находятся из выражений

а₀= Σ у_t / п; а ₁ = Σ у_t t / Σ t ². (6.4)

Аналогично определяются коэффициенты полинома второй степени (параболы), которые после переноса начала координат в середину ряда динамики имеют вид

a₀ = Σ y _t / n – Σ t ² / {(n Σ y _t t ² – Σ t ² Σ y _t) / [ n Σ t ⁴ – (Σ t ²) ² ]};

a₁ = Σ y _t t / Σ t ² ; a₂ = (n Σ y _t t ² – Σ t ² Σ y _t) / [ n Σ t ⁴ – (Σ t ²) ²];

 

Показательная кривая (рис. 6.4) имеет следующий вид.

 

 

 

Рис. 6.4. Экспонента у _t = а b ^t.

Если b > 1, то кривая растет с ростом t и падает, если b<1. Параметр а характеризует начальные условия, а параметр b — постоянный темп роста.

Прологарифмировав это выражение, получим:

lоg у _t = lоg а + t ∙ lоg b.

Обозначим A = lоg а, В = lоg b,тогда lоg y _t = А + t∙В. Для оценивания неизвестных параметров можно использовать систему нормальных уравнений для прямой и найти параметры А и В. Зная значения

A = lоg а и В = lоg b, путем потенцирования определим значения а и b.

Следует иметь в виду, что полученные таким образом оценки пара­метров показательной кривой оказываются смещенными в связи с тем, что в расчете участвуют не исходные данные, а их логарифмы. Причем смещение будет тем значительнее, чем больше разность меж­ду соседними уровнями заданного ряда.

Рассмотренные типы кривых используются для описания монотон­но возрастающих или убывающих процессов без насыщения. Примером кривой с насыщением является модифицированная экспонента (рис. 6.5)

y _t = k + a b ^t, (6.5)

 

 

где у = k — горизонтальная асимптота.

 

 

 

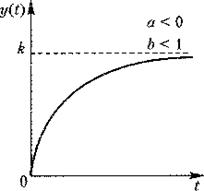
Рис. 6.5. Модифицированная экспонента y _t = k + a b ^t

Коэффициент k может быть определен исходя из свойств прогнози­руемого процесса или задан экспертным путем. В этом случае пара­метры кривой могут быть определены с помощью метода наименьших квадратов после приведения уравнения к линейному виду

y _t - k ₁ = a b ^t,

где k ₁, — заданное значение асимптоты. После логарифмирования это­го выражения получаем:

lоg (у _t – k ₁ ) = lоg а + t lоg b.

Используя систему нормальных уравнений, можно найти параметры lоg а и lоg b, потенцирование которых определяет а и b. Если параметр а отрицателен, то асимптота расположена выше кривой.

В экономических процессах чаще всего используется случай, когда

а < 0, b < 1. При этом рост уровней ряда замедляется и стремится к некоторому пределу.

Наиболее известными из S-образных кривых являются кривая Гомперца (рис. 6.6) и логистическая кривая (кривая Перла — Рида) (рис. 6.7).

 

 

 

Рис. 6.6. Кривая Гомперца у _t = k a ^bt

Кривая Гомперца имеет аналитическое выражение

у _t = k a ^b (6.6)

где а, b — положительные параметры, причем b меньше единицы; у = k — асимптота функции.

Для решения экономических задач чаще всего используется случай, когда lоg а < 0, b < 1.

Рис. 6.7. Логистическая кривая 1 /y ^t = k + a b ^t

В кривой Гомперца выделяются четыре участка: на первом прирост функции незначителен, на втором прирост увеличивается, на третьем прирост примерно постоянен, на четвертом происходит замедление темпов прироста и функция неограниченно при­ближается к значению k. В результате кривая напоминает латинскую букву S.

 

Логистическая кривая (кривая Перла — Рида) — возрастающая функция, наиболее часто выражаемая в виде

1 / y _t = k + a b ^t, (6.7)

используется и другой вид кривой

y _t = k / ( 1 + b e ^{– at}).

В этих выражениях y _t = а и b — положительные параметры, k — предельное значение функции при стремлении t →∞. Конфигурация графика логистической кривой близка к графику кривой Гомперца, но в отличие от нее логистическая кривая имеет точку симметрии, совпадающую с точкой перегиба. С помощью этой функции хорошо описывается развитие нового производства. В начале производства нового вида товара технические средства производства еще недостаточно разработаны, издержки производства высоки и спрос на товар мал. В дальнейшем, с увеличением спроса и усовершенствованием технических методов изготовления, производство товаров увеличивается. Наступает насыщение товаров на рынке, рост производства замедляется и наступает стабилизация выпуска товаров на определенном уровне,

Рассмотренные кривые роста, наиболее часто используемые в эко­номических исследованиях, могут оказать помощь при выборе типа кривой.

Существует ряд подходов, облегчающих выбор кривой роста. Это, в первую очередь, статистические методы, например, метод последовательных разностей, метод характеристик прироста. Часто кривую роста выбирают исходя из значений критерия, в качестве которого принимают минимальное значение суммы квадратов отклонений фактических значений уровня от расчетных.

Однако нельзя недооценивать наиболее простой метод — визуальный. Подбирают кривую роста, форма которой соответствует реальному процессу. Если на графике временного ряда недостаточно просматри­вается тенденция развития, то следует провести сглаживание ряда и затем подобрать кривую, соответствующую новому ряду. При этом целесообразно использовать современные пакеты компьютерных программ.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ:

1. Как подразделяются прогнозы в зависимости от глубины упреждения?

2. Каким образом определяются доверительные границы значений прогнозируемой величины?

 

Заключение

Систематизация знаний о закономерностях построения (проектирования) рациональных процессов изготовления объекта производства является основой создания математических моделей информационной базы технологического назначения. Проектирование технологического процесса содержит две составляющие: структурную и параметрическую. Наиболее сложной для формализации является задача структурной оптимизации. Моделирование как инструмент исследования позволяет дать сжатое и точное описание всех технических систем, связанных с проектированием технологий. Взаимосвязь технических систем проявляется во взаимосвязи структур геометрических связей. Перспектива состоит в раскрытии закономерностей и построении моделей для реализации многофакторных и многокритериальных задач синтеза структуры технологического процесса. Решение указанных задач позволит управлять качеством технологических процессов на стадии их проектирования.

 

 

Библиографический список

Основной:

1. Кузьмин, В.В. Математическое моделирование технологических процессов сборки, механической обработки изделий в машиностроении: учеб. пособие / В.В. Кузьмин. - М.: Высш. шк., 2008.

2. Красс, М.С. Математика для экономистов: учеб. пособие для вузов/ М.С. Красс, Б.П. Чупрынов. - СПб.: Питер, 2007.

 

Дополнительный:

3. Бережная, Е.В. Математические методы моделирования экономических систем: учеб. пособие для вузов /Е.В. Бережная, В.И. Бережной. - М.: Финансы и статистика.2003.

4. Адлер, Ю.П. Планирование эксперимента при поиске оптимальных условий. Программированное введение в планирование эксперимента: учебник / Ю.П. Адлер, Е.В. Маркова, Ю.В. Грановский. - М.:Наука, 1971.

5. Кузнецов, О.П. Дискретная математика для инженера / О.П. Кузнецов, Г.М. Адельсон-Вельский. – 2-е изд., перераб. и доп. - М.: Энергоатомиздат, 1988.

6. Челищев, Б.Е. Автоматизация проектирования технологии в машиностроении /Б.Е. Челищев, И.В. Боброва, А. Гонсалес-Сабатер; под ред. Н.Г. Бруевича. – М.: Машиностроение, 1987.

 

Средства обеспечения освоения дисциплины (ресурсы Internet):

7. http:/www.mathsoft.com

8. http:/www.informika.ru

9. http://www.window.edu.ru

10. http:/www.exponenta.ru

11. http:/www.elib.nwpi.ru

 

Предметный указатель

А

взаимно однозначное соответствие 45

аналитический способ задания функции 14, 72

алгоритм 82, 89,90

адекватность математической модели 19

алгебра логики 90

асимптота 115

В

временный 8, 10, 13, 106

вершина графа 29

Г

граф ориентированный 26

граница множества 25

граф 29, 49, 52, 54, 117

граф изоморфный 80

граф конечный 93

Д

динамические 106

З

закон нормального рассеивания 37

закон распределения 36, 40, 51, 93

К

конъюнкция 67

дизъюнкция 67

кривая рассеивания 37

кривая распределения 43

корреляция 92

Л

линейная 93, 98

логическая 66, 90

М

маршрут в графе 28

множество 21, 66, 70, 75

моделирование 2, 31, 118

модель 5, 9, 11, 101

Н

нелинейная 98, 101

несвязное 22

неравнозначная 67

О

оптимизация 47

объект 2, 47, 71, 105

П

погрешность 19, 37, 41, 58

предикаты 69

процесс 2, 15, 33, 157, 70, 105

прогноз 110

Р

ребро 25

размерный анализ 30

размерный синтез 32

регрессия 91, 98, 104

ряды 106

С

совместности 71, 77

следования 74, 17, 37, 71, 101

систематические 34

случайные 34, 46, 92, 107

система 4, 34, 99

Т

тренд 108

Ф

функция 14, 46, 64, 86,104

Ц

цепь 25

цикл 28, 44

Э

элементы 6, 21, 71

экономичность 20

эксперимент 5, 15, 35, 55

эквивалентная 69

экспонента 104, 114

 

Оглавление

Предисловие. 3

Конспект лекций. 4

Раздел 1. Введение. Задачи и объекты математического моделирования в машиностроительном производстве ……………………………………………….4

1.1. Задачи моделирования. Виды моделей. 5

1.2. Классификация моделей. 11

1.3. Требования к математическим моделям……………………………….......18

Раздел 2. Моделирование дискретных объектов и процессов. 20

Раздел 3 Графы. Использование графов для моделирования технических систем ……………………………………………………………………………25

 

Раздел 4. Моделирование с использованием элементов теории вероятностей. 33

4.1Статистические исследования в задачах оценки точности. 33

4.2 Теория вероятности при оценке надежности технических систем. 47

4.3 Планирование эксперимента…………………………………………….......56

Раздел 5. Моделирования процессов принятия решений. 66

5.1. Логические модели представления знаний. 66

5.2. Исчисление предикатов. 70

5.3. Элементы теории принятия решений. Алгоритмы поиска решений……….77

Раздел 6. Моделирование экономических процессов. 91

6.1. Линейная и нелинейная регрессия. 91

6.2. Прогнозирование экономических процессов. 104

Заключение……………………………………..………………………………….117

 

Библиографический список…………………………………..…………………..118

 

Редактор А.В.Алехина

 

 

Сводный темплан 2001 г.

Лицензия ЛР №020308 от 14.12.97

__________________________________________________________

 

Подписано в печать Формат 60´84 1/16

 

Б. кн. – журн. П.л. 1.25 Б.л. 0,625 РТП РИО СЗТУ

 

Тираж 120 Заказ

 

__________________________________________________________

Северо-Западный государственный заочный технический университет

РИО СЗТУ, член Издательско-полиграфической ассоциации вузов Санкт-Петербурга

191186, Санкт-Петербург, ул. Миллионная, 5